【LeetCode热题100】79. 单词搜索（回溯）

news2024/11/26 3:45:22

一.题目要求

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

二.题目难度

中等

三.输入样例

示例 1：
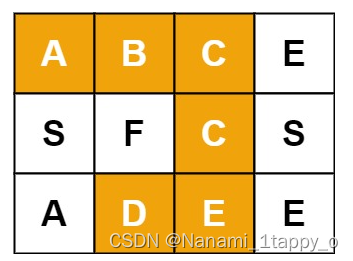
在这里插入图片描述
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出：true

示例 2：
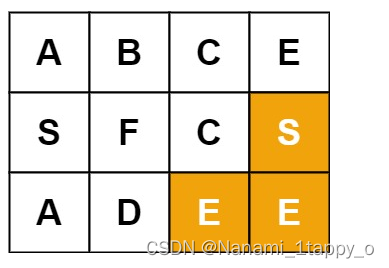
在这里插入图片描述
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
输出：true

示例 3：
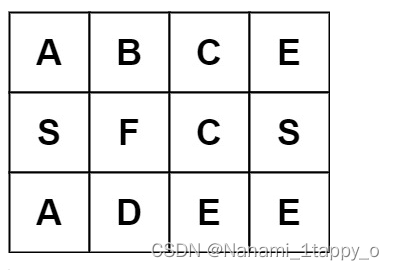
在这里插入图片描述
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
输出：false

提示：
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

四.解题思路

存不存在问题最好用bool型递归，不然时间差很多

五.代码实现

用void返回，找到了也会继续递归判断完所有条件

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        string path;
        vector<vector<bool>> used(board.size(), vector<bool>(board[0].size()));
        for (int i = 0; i < board.size(); i++) {
            for (int j = 0; j < board[0].size(); j++) {
                dfs(board, word, used, i, j, 0);
                if (finded)
                    return true;
            }
        }
        return finded;
    }

    void dfs(vector<vector<char>>& board, string word,
             vector<vector<bool>>& used, int x, int y, int step) {
        if (finded)
            return;
        if (word.size() == step) {
            finded = true;
            return;
        }
        if (x >= board.size() || x < 0)
            return;
        if (y >= board[0].size() || y < 0)
            return;
        if (used[x][y])
            return;
        if (word[step] != board[x][y])
            return;

        step++;
        used[x][y] = true;

        dfs(board, word, used, x - 1, y, step);
        dfs(board, word, used, x, y + 1, step);
        dfs(board, word, used, x + 1, y, step);
        dfs(board, word, used, x, y - 1, step);
        used[x][y] = false;
    }

private:
    bool finded = false;
};

在这里插入图片描述
bool型，只要找到一种满足的就直接终止后续递归

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        string path;
        vector<vector<bool>> used(board.size(), vector<bool>(board[0].size()));
        for (int i = 0; i < board.size(); i++) {
            for (int j = 0; j < board[0].size(); j++) {
                if (dfs(board, word, used, i, j, 0))
                    return true;
            }
        }
        return false;
    }

    bool dfs(vector<vector<char>>& board, string& word,
             vector<vector<bool>>& used, int x, int y, int step) {
    
        if (word.size() == step) 
            return true;
        
        if (x >= board.size() || x < 0 || y >= board[0].size() || y < 0 || used[x][y] || word[step] != board[x][y])
            return false;
        step++;
        used[x][y] = true;
        bool result = dfs(board, word, used, x - 1, y, step) || 
        			  dfs(board, word, used, x, y + 1, step) || 
        			  dfs(board, word, used, x + 1, y, step) || 
        			  dfs(board, word, used, x, y - 1, step);
        used[x][y] = false;

        return result;
    }


};

在这里插入图片描述

六.题目总结

1.能传引用传引用
2.二维数组初始化：vector<vector> used(board.size(), vector(board[0].size()));
3.

for (int i = 0; i < board.size() && !found; i++) {
            for (int j = 0; j < board[0].size() && !found; j++) {
                dfs(board, word, used, i, j, 0);
            }
}