目录
一、什么是bfs
二、bfs和dfs的差异
搜索顺序:
数据结构:
搜索方式:
三、bfs解决的主要问题
四、例题
一、什么是bfs
BFS(广度优先搜索)是一种图搜索算法,用于在图或树数据结构中进行遍历。BFS从根节点开始,沿着图的宽度遍历图的顶点,直到找到目标顶点或遍历完所有顶点。在BFS中,首先访问根节点,然后依次访问与根节点相邻的节点,再依次访问这些相邻节点的邻居节点,以此类推。BFS通常使用队列数据结构来实现。
BFS的基本思想是将当前节点的所有邻居节点都加入到队列中,然后逐个访问队列中的节点,并将它们的邻居节点加入队列。这样可以保证先访问距离当前节点较近的节点,从而实现按层级遍历。
在计算机科学中,BFS常用于解决图的最短路径问题(迷宫问题)、连通性(连通块数量、大小问题)
二、bfs和dfs的差异
-
搜索顺序:
- BFS:从起始节点开始,先访问所有与起始节点相邻的节点,然后再逐层向外扩展。在同一层级上,所有节点都会被访问后才会继续向下一层级搜索。
- DFS:从起始节点开始,沿着一条路径一直向深处搜索,直到到达叶子节点,然后回溯到上一个节点,继续搜索其他路径。
-
数据结构:
- BFS:通常使用队列(Queue)数据结构来实现,因为BFS需要按照先进先出的顺序访问节点。
- DFS:通常使用栈(Stack)数据结构来实现,因为DFS需要回溯到上一个节点。
-
搜索方式:
- BFS:适合用于寻找最短路径或最短距离的问题,因为BFS会先访问离起始节点最近的节点。
- DFS:适合用于寻找所有可能路径的问题,因为DFS会一直向深处搜索,直到找到所有路径。
其实举个例子就能很好的总结,假如我们有一个迷宫告诉你起点和终点,bfs从起点开始逐步向外扩张,dfs则是一个一个试过去。从结果来看dfs是把所有路径都走了一遍,各种各样的组合都有,而bfs只能是第一步能到达的、第二步能到达的.......。
三、bfs解决的主要问题
BFS(广度优先搜索)可以解决许多与图相关的问题,其中一些主要的问题包括:
1. 最短路径问题:BFS可以用于查找从一个节点到另一个节点的最短路径,因为BFS按照层级遍历的方式逐步扩展搜索范围,可以保证先找到的路径是最短的。
2. 连通性问题:BFS可以用于确定图中两个节点是否连通,即是否存在一条路径连接这两个节点。
3. 拓扑排序问题:BFS可以用于进行拓扑排序,即对有向无环图(DAG)中的节点进行排序,使得所有的边从排在前面的节点指向排在后面的节点。
4. 最小生成树问题:BFS可以用于查找最小生成树,如Prim算法中的一部分就是利用BFS来查找最小生成树。
5. 能否到达问题:BFS可以用于判断从一个节点是否可以到达另一个节点,或者判断某个节点是否 可以到达图中的所有其他节点。
总的来说,BFS是一个非常通用且强大的图搜索算法,可以应用于许多不同类型的问题,特别是那些涉及路径查找、连通性、排序等方面的问题。
四、例题
链接:https://sunnywhy.com/sfbj/8/2/324
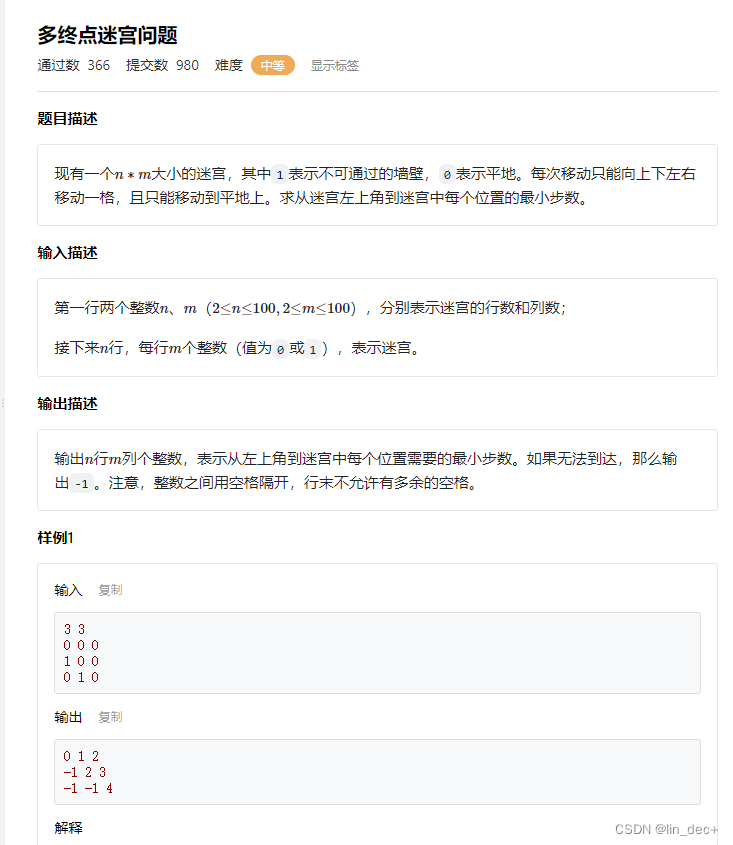
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=100;
bool isvalid[maxn][maxn]={false}; // 记录每个位置是否已经访问过
int maze[maxn][maxn]; // 迷宫地图
vector<vector<int>> ans(maxn,vector<int> (maxn,-1)); // 存储每个位置的步数
int dx[4]={1,-1,0,0}; // x方向的四个移动方向
int dy[4]={0,0,1,-1}; // y方向的四个移动方向
int n,m; // 迷宫的行数和列数
struct position{
int x,y,step; // 位置的坐标和步数
};
void bfs(int start_x,int start_y){
queue<position> q; // 定义一个队列用于BFS
position start={start_x,start_y,0}; // 起始位置
q.push(start); // 将起始位置加入队列
isvalid[start_x][start_y]=true; // 标记起始位置已访问
while(!q.empty()){
position front=q.front(); // 取出队首位置
q.pop(); // 弹出队首位置
ans[front.x][front.y]=front.step; // 记录当前位置的步数
for(int i=0;i<4;i++){ // 遍历四个方向
int cx=front.x+dx[i]; // 计算下一个位置的x坐标
int cy=front.y+dy[i]; // 计算下一个位置的y坐标
if(cx>=0 && cx<n && cy>=0 && cy<m && maze[cx][cy]==0 && isvalid[cx][cy]==false){ // 判断下一个位置是否合法
position cur={cx,cy,front.step+1}; // 下一个位置的信息
q.push(cur); // 将下一个位置加入队列
isvalid[cx][cy]=true; // 标记下一个位置已访问
}
}
}
}
int main(){
cin>>n>>m; // 输入迷宫的行数和列数
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>maze[i][j]; // 输入迷宫地图
}
}
bfs(0,0); // 从起始位置开始BFS
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
printf("%d", ans[i][j]); // 输出每个位置的步数
printf(j < m - 1 ? " " : "\n"); // 格式化输出
}
}
return 0;
}