前言
大家好,我是jiantaoyab,开始刷动态规划的子数组类型相关的题目
动态规划5个步骤
- 状态表示 :dp数组中每一个下标对应值的含义是什么>dp[i]表示什么
- 状态转移方程: dp[i] 等于什么
- 1 和 2 是动态规划的核心步骤,第三步是初始化,保证填表的时候不越界
- 填表顺序:为了保证填写当前状态的时候,所需要的状态已经计算过
- 返回值
最大子数组和

题目分析
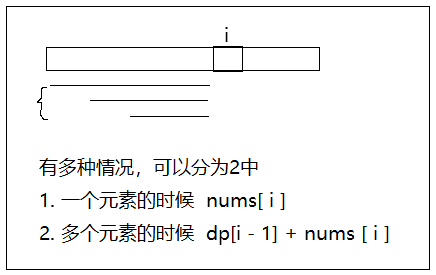
dp[i] : 到达 i 位置所有子数组中的最大和
dp[i] = max(nums[i], dp[i - 1] + nums[i]);
初始化:新增加一个数初始化为0
返回值:dp表中最大的元素
代码
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n + 1);
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
ret = max(ret, dp[i]);
}
return ret;
}
};
环形子数组的最大和

题目分析
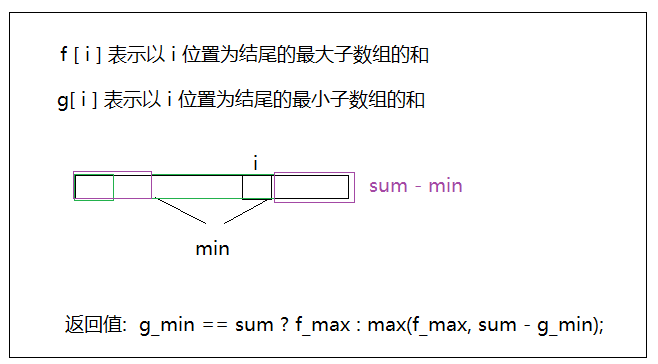
代码
class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1);
vector<int> g(n + 1);
int f_max = INT_MIN;
int g_min = INT_MAX;
int sum = 0;
for(int i = 1; i <= n; i++)
{
sum += nums[i - 1];
f[i] = max(nums[i - 1], f[i - 1] + nums[i - 1]);
f_max = max(f_max, f[i]);
g[i] = min(nums[i - 1], g[i - 1] + nums[i - 1]);
g_min = min(g_min, g[i]);
}
// g_min == sum 说明数组里面全是负数
return g_min == sum ? f_max : max(f_max, sum - g_min);
}
};
乘积最大子数组

题目分析

代码
class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1);
vector<int> g(n + 1);
f[0] = g[0] = 1;
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
f[i] = max(max(f[i - 1] * nums[i - 1], g[i - 1]* nums[i - 1]), nums[i - 1]);
g[i] = min(min(f[i - 1] * nums[i - 1], g[i - 1]* nums[i - 1]), nums[i - 1]);
ret = max(ret, f[i]);
}
return ret;
}
};
乘积为正数的最长子数组长度

题目分析

初始化: f[0] = g[0] = 0;
返回值:返回f[i] 中的最大值
代码
class Solution {
public:
int getMaxLen(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1);
vector<int> g(n + 1);
int ret = INT_MIN;
for(int i = 1; i <= n; i++)
{
if(nums[i - 1] > 0)
{
f[i] = f[i - 1] + 1;
g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
}
else if(nums[i - 1] < 0)
{
f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
g[i] = f[i - 1] + 1;
}
ret = max(ret, f[i]);
}
return ret;
}
};
等差数列划分

题目分析

代码
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n);
int count = 0;
for(int i = 2; i < n; i++)
{
int x = nums[i - 2];
int y = nums[i - 1];
int z = nums[i];
dp[i] = y - x == z - y ? dp[i - 1] + 1 : 0;
count += dp[i];
}
return count;
}
};
最长湍流子数组

题目分析
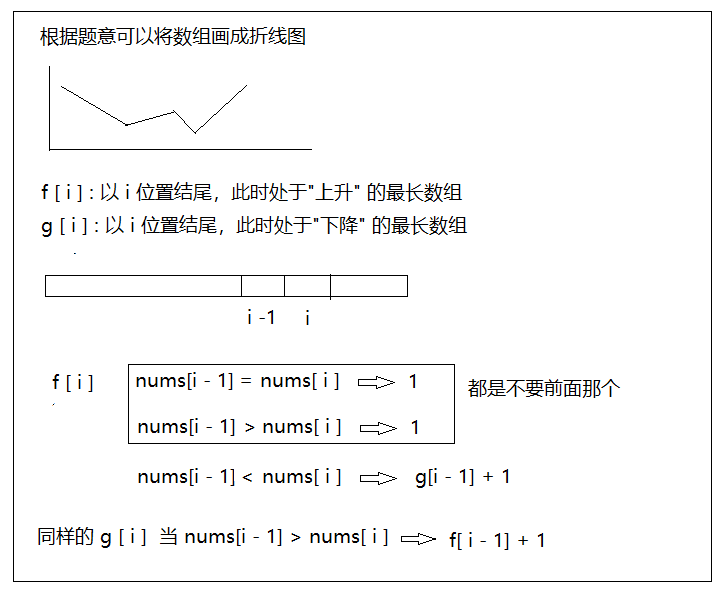
初始化:都初始化为1,再去填就好了
返回值:返回的是f 表 和 g表中最大的值
代码
class Solution {
public:
int maxTurbulenceSize(vector<int>& arr) {
int n = arr.size();
vector<int>f(n, 1);
vector<int>g(n, 1);
int g_max = 1, f_max = 1;
for(int i = 1; i < n; i++)
{
if(arr[i - 1] > arr[i] )
{
g[i] = f[i - 1] + 1;
g_max = max(g_max, g[i]);
}
else if(arr[i - 1] < arr[i])
{
f[i] = g[i - 1] + 1;
f_max = max(f_max, f[i]);
}
}
return g_max > f_max ? g_max : f_max;
}
};
单词拆分

题目分析

代码
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> hash;
for(auto& str : wordDict) hash.insert(str);
int n = s.size();
vector<bool> dp(n + 1);
dp[0] = true;
s = ' ' + s; //字符串下标统一 + 1
for(int i = 1; i <= n; i++)
{
for(int j = i; j >= 1; j--) //找最后一个单词的起始位置
{
if(dp[j - 1] && hash.count(s.substr(j, i - j + 1)))
{
dp[i] = true;
break;
}
}
}
return dp[n];
}
};
环绕字符串中唯一的子字符串
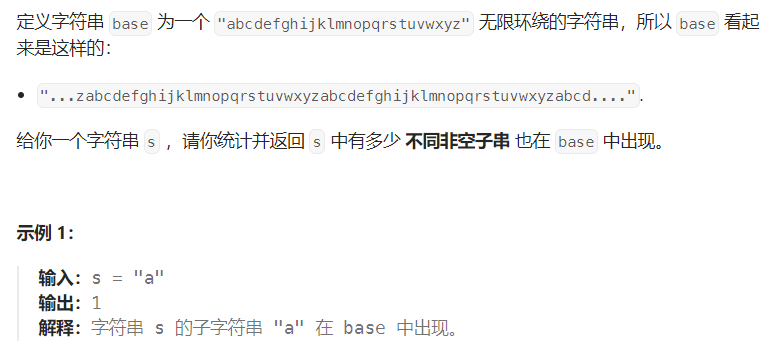
题目分析

代码
class Solution {
public:
int findSubstringInWraproundString(string s) {
int n = s.size();
vector<int> dp (n, 1);
for(int i = 1; i < n; i++)
{
if(s[i - 1] + 1 == s[i] || (s[i - 1] == 'z' && s[i] == 'a'))
{
dp[i] += dp[i - 1];
}
}
int hash[26] = {0};
for(int i = 0; i < n; i++)
{
hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);
}
int sum = 0;
for(auto x : hash) sum += x;
return sum;
}
};