论文：Text2QR: Harmonizing Aesthetic Customization and Scanning Robustness for Text-Guided QR Code Generation

Abstract

二维码通常包含很多信息但看起来并不美观。stable diffusion的出现让平衡扫描鲁棒性和美观变为可能。
为了保证美观二维码的稳定生成，引入了QR美观蓝图(QR Aesthetic Blueprint, QAB)模块，生成蓝图图像，对整个生成过程进行控制。随后，可扫描性增强潜在细化(the Scannability Enhancing Latent Refinement, SELR)过程在潜在空间内细化输出，从而强化了可扫描的鲁棒性。
这个方法利用了stable diffusion的强大生成能力，在图像美观性和二维码可扫描行之间进行权衡。

Github仓库

1 Introduction

现在有很多工作致力于改善二维码的美观性，但是大多导致了扫描的不稳定。

本文提出了Text2QR，提供无缝生成二维码的解决方案，平衡用户定义的美观性和强大的可扫描性。
框架通过三个关键步骤展开：

• 用户通过使用stable diffusion生成他们喜欢的图案来启动该流程。
• 协同作用开始于QAB模块中图像的混合。这个模块生成一张蓝图，合并预先生成的图像（引导图像）中的内容，并准确反映QR码中的编码信息。然后将这张蓝图图像输入ControlNet，指导Stable Diffusion保留用户定义的美观性，并维持QR码明暗块之间的所需关系。虽然生成的结果会带来解码挑战，但是其表现出明显的明暗块分布，同时保持与用户偏好一致。
• 构建了能量方程，量化生成结果中的内容和消息的一致性。通过对潜在代码进行梯度上升迭代来优化该能量方程，逐渐增强扫描鲁棒性，同时保持内容一致性。

本文的贡献：

• Text2QR，在二维码生成中协调用户定义的美观性和强大的可扫描性。
• 引入QAB模块和SELR流程，用于保持美观的同时优化扫描稳健性。
• 更优越的效果

3 Preliminary

先阐明QR码扫描仪从美观的QR码图像中解码二进制信息的过程。
给定带有QR码的彩色图像，首先通过提取亮度通道（YCbCr颜色空间中的Y通道），将其转化为灰度表示，表示为$I\in {\mathbb{R}}^{H\times W}$，包含$L$个灰度级（通常为256）。
设QR码包含$n\times n$个模块，每个模块的大小为$a\times a$个像素，有$n\cdot a\le \min (H,W)$。这样就构建出了一个包含$n^2$个模块的网格，记作$M_k$，其中$k\in [1,2,\cdots ,n^2]$。这个网格将图像$I$划分为$n^2$个块，表示为$I_{M_k}\in {\mathbb{R}}^{a\times a}$。

第$k$个模块被解码为1位信息${\tilde{I}}_k$，代表0或1，其中$\tilde{I}\in {\mathbb{R}}^{n\times n}$表示整张二进制图的结果。
通常扫描仪对于每个模块的中心子区域内的像素进行采样。
令$\theta$为以模块$M_k$为中心、大小为$x\times x$的正方形区域， p ∈ { 1 , 2 , ⋯   , H } × { 1 , 2 , ⋯   , W } \mathbf{p}\in\{1,2,\cdots,H\}\times \{1,2,\cdots,W\} p∈{1,2,⋯,H}×{1,2,⋯,W}表示$I$的像素坐标。解码后的二进制值${\tilde{I}}_k$可以记作：
$$v_k=\frac{1}{x^2}\sum _{\mathbf{p}\in \theta }{I}_{M_k}(\mathbf{p});{\tilde{I}}_k=\{\begin{array}{ll}0& \text{if}{v}_k\le {\mathcal{T}}_b,\\ 1& \text{if}{v}_k\ge {\mathcal{T}}_w,\\ -1& \text{otherwise}.\end{array}$$
其中${\mathcal{T}}_b$和${\mathcal{T}}_w$是二值化的阈值。考虑到对称性，令${\mathcal{T}}_b=L\cdot (1-\eta )/2$，${\mathcal{T}}_w=L\cdot (1+\eta )/2$，其中$\eta \in (0,1)$。超参数$\eta$可以控制二值化过程的严格性。

4 Method

4.1 Overall

第一阶段，用户准备$I^g$和$\mathcal{M}$（依赖关联参数$c$和$z_0$）。
第二阶段，关键一步是通过创新的QAB模块将$I^g$和$\mathcal{M}$中封装的信息无缝集成，以制定全面的蓝图，记为$I^b$。
随后，$I^b$在ControlNet $\mathcal{C}$中进行处理，以对stable diffusion model施加影响。这个影响涉及通过受控过程调整中间特征，定义为：
$$I^s=\mathcal{G}(c,z_0|\mathcal{C}(I^b,c,z_0))$$
这种整合确保了协同输出$I^s$和谐地平衡了源自$I_g$的审美偏好和$\mathcal{M}$的结构约束。
最后阶段，$I^s$通过SELR模块进行迭代微调，改进了扫描鲁棒性，同时保留了美术品质。

最后输出是一个美观的二维码$Q$。

4.2 QR Aesthetic Blueprint

该模块旨在通过集成二维码信息和引导图像细节来创建可扫描的蓝图。

最初，从引导图像$I^g$中提取亮度通道，表示为$I_y^g$。为了确保可以比较的分布，分别使用直方图偏振(Histogram polarization)进行亮度调整和模块重组的方法进行像素重新排列来预处理$I_y^g$和$\mathcal{M}$。最后，应用自适应半色调方法(Adaptive-Halftone)将二者混合，产生蓝图图像$I^b$。

4.2.1 Histogram polarization

该模块的主要目的是协调$I_y^g$的直方图分布和QR码的直方图分布。该过程增强了$I_y^g$的对比度，产生高对比度的图像$I^{hc}$。
直方图偏振操作由查找表$\mathcal{H}$表示，其将像素值从一个灰度级映射到另一个灰度级。

对于每一个像素$\mathbf{p}$，令$\tau =I_y^g(\mathbf{p})$，${\tau }^{\prime }=I^{hc}(\mathbf{p})$，将过程表示为：
$${\tau }^{\prime }=\mathcal{H}(\tau )$$
令$n_{\tau }$表示灰度级$\tau \in [0,L)$的出现次数，为每一个灰度级$\tau$引入累积分布函数(Cumulative Distribution Function, CDF)：
$$\text{cdf}(\tau )=\sum _{i=0}^{\tau }\frac{n_i}{H\times W}$$
目标是令生成的$I^{hc}$在$[0,{\mathcal{T}}_b)\cup [{\mathcal{T}}_w,L)$范围内具有平坦的直方图。同时排除在$[{\mathcal{T}}_b,{\mathcal{T}}_w)$中出现的情况。为了实现这一点，首先创建一个新图像$I^{he}$，其线性化CDF的值的范围为$[0,L-{\mathcal{T}}_w+{\mathcal{T}}_b)$。令$\tilde{\tau }=I^{he}(\mathbf{p})$，于是有：
$$\tilde{\tau }=(L-{\mathcal{T}}_w+{\mathcal{T}}_b)\cdot \text{cdf}(\tau )$$
随后，通过添加${\mathcal{T}}_w-{\mathcal{T}}_b$来移动值的范围$[{\mathcal{T}}_b,L)$从而获得$I^{hc}$：
$${\tau }^{\prime }=\mathcal{H}(\tau )=\{\begin{array}{ll}\tilde{\tau }& \text{if}\tilde{\tau }<{\mathcal{T}}_b,\\ \tilde{\tau }+{\mathcal{T}}_w-{\mathcal{T}}_b& \text{if}\tilde{\tau }\ge {\mathcal{T}}_b.\end{array}$$

4.2.2 Module reorganization

为了将QR码$\mathcal{M}$与$I^{hc}$混合，首先将$I^{hc}$二值化为二值图像$I^{bin}$。该二值图像指导module reorganization方法，记为${\mathcal{E}}_r$，该方法在保留编码信息的同时重新排列$\mathcal{M}$的模块。该过程可以表述为：
$$I^{bin}(\mathbf{p})=\{\begin{array}{ll}0& \text{if}{I}^{hc}(\mathbf{p})<{\mathcal{T}}_b,\\ 1& \text{if}{I}^{hc}(\mathbf{p})>{\mathcal{T}}_w,\end{array}$$
$${\mathcal{M}}^r={\mathcal{E}}_r(\mathcal{M},I^{bin})$$

4.2.3 Adaptive-Halftone blending

考虑第$k$个模块区域$M_k$，我们输入经过histogram polarization后的图像块$I_{M_k}^{hc}$和一个目标值$M_k^r=0\text{or}1$。目标是获得蓝图$I^b$，其中$I_{M_k}^b$可以被解码为正确的信息，同时保留尽可能多的图像内容。

为了达成这个目标，引入了全新的blending method：Adaptive-Halftone blending(自适应半色调混合)。
具体地，对于每个模块$M_k$，令${\theta }_k$是一个大小为$u\times u$的方形区域，以图像块$I_{M_k}^{hc}(u\le a)$为中心。用${\mathcal{M}}_k^r$来填充$I_{{\theta }_k}^{hc}$以生成$I_{M_k}^b$。通过最小化该模块内的编码距离来优化放行区域大小$u$。$u$对应的该模块的模拟解码值定义为$E_k(I_{M_k}^b|u)$：
$$\begin{array}{rl}{E}_k(I_{M_k}^b|u)& =\frac{1}{a^2}[\sum _{\mathbf{p}\in {\theta }_k}L\cdot {\mathcal{M}}_k^r+\sum _{\mathbf{p}\notin {\theta }_k}{I}_{M_k}^b(\mathbf{p})]\\ & =\frac{1}{a^2}[u^2\cdot L\cdot {\mathcal{M}}_k^r+\sum _{\mathbf{p}\notin {\theta }_k}{I}_{M_k}^b(\mathbf{p})]\end{array}$$
特别地，当$u=a$时，有$E_k(I_{M_k}^b|u)=L\cdot {\mathcal{M}}_k^r$。目标是最小化编码距离：
$$u_k=\underset{v}{\mathrm{argmin}}||E_k(I_{M_k}^b|u)-L\cdot (\eta \cdot {\mathcal{M}}_k^r+\frac{1-\eta }{2})||$$
根据${\mathcal{T}}_b$和${\mathcal{T}}_w$的定义，可以简写上式：
$$s_k=\{\begin{array}{ll}\underset{s}{\mathrm{argmin}}||E_k(I_{M_k}^b|u)-{\mathcal{T}}_b||& \text{if}{\mathcal{M}}_k^r=0,\\ \underset{s}{\mathrm{argmin}}||E_k(I_{M_k}^b|u)-{\mathcal{T}}_w||& \text{if}{\mathcal{M}}_k^r=1,\end{array}$$
为每个模块都填充了合适尺寸的同心方形块后，继续将标记（包括查找器和对齐标记）粘贴到最终的蓝图$I^b$上。

下图展示了从不同的蓝图生成不同的$I^s$：

此调整涉及当$I^{hc}$有效封装模块信息以保留更多图像内容时缩小块的大小。
相反，当需要更明显的控制信号来确保模块在$I^s$中的可扫描性时，它会扩大块的大小。

4.3 Scannability Enhancing Latent Refinement

生成的$I^s$遵循施加的${\mathcal{M}}^r$的结构约束，但因为仍有大量错误的模块，因此不可扫描。为了解决此问题，可扫描性增强潜在细化(Scannability Enhancing Latent Refinement, SELR)提供了很细致的强化过程来增强扫描鲁棒性。

包括取景器和对其图案的标记对于确定QR码的位置和角度至关重要，从而影响其扫描性。因此，在细化之前将它们的外观整合到$I^s$上，记作$\widehat{I^s}$。

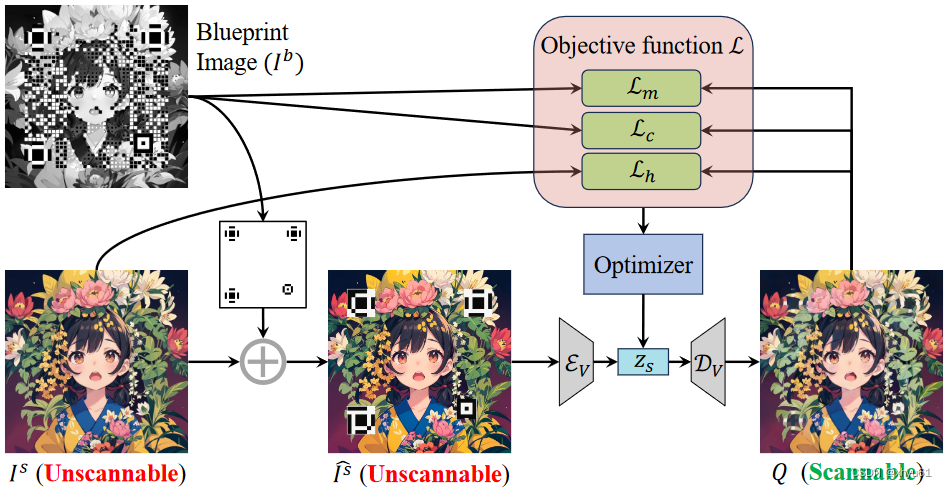
使用VAE将增强图像$\widehat{I^s}$编码为潜在代码$z_s$，将VAE的模型记作${\mathcal{E}}_V$。总体目标函数$L$可以被分为三项之和：标记损失${\mathcal{L}}_m$，编码损失${\mathcal{L}}_c$，协调损失${\mathcal{L}}_h$。
$$\begin{array}{rl}\mathcal{L}(z)& ={\lambda }_1{\mathcal{L}}_m({\mathcal{D}}_V(z),I^b)\\ & +{\lambda }_2{\mathcal{L}}_c({\mathcal{D}}_V)(z),I^b)\\ & +{\lambda }_3{\mathcal{L}}_h({\mathcal{D}}_V)(z),I^s)\end{array}$$
其中，${\lambda }_1$到${\lambda }_3$用于平衡各项之间的权重。${\mathcal{D}}_V$代表VAE编码器的解码器。$z$是由$z_s$初始化并在不断迭代中通过最小化目标函数来微调的潜变量，控制生成的QR码$Q={\mathcal{D}}_V(z)$的可扫描性和美观质量。代码损失${\mathcal{L}}_c$是通过Artcoder: an end-to-end method for generating scanning-robust stylized qr codes这篇文章提出的方法计算的，该方法采用SSLayer提取模块值，通过竞争机制计算基于模块的代码损失。

4.3.1 Marker loss

扫描仪根据标记区域中的特定像素比来识别QR码。
引入一个二元掩码${\mathcal{K}}_{cc}$，专门用于过滤标记的交叉中心区域，目的是保护基本标记功能免受因美学定制而造成的潜在损害。形式上，标记损失函数${\mathcal{L}}_m$定义如下：
$${\mathcal{L}}_m(Q,I^b)={\mathcal{K}}_{cc}\cdot ||Q_y-I^b|{|}^2$$
其中$Q_y$表示二维码$Q$的亮度通道。
这个公式确保了标记的完整性，同时允许对QR码的非标记区域进行美观修改。重点是优化视觉质量，同时保持原始扫描能力。

这个损失函数计算了$L^2$-Wasserstein距离，记为$W_2$，计算$Q$的特征图和$I^s$的距离。
特别地，

4.3.2 Harmonizing Loss

解决了与标记和代码相关的可扫描性问题后，要进一步确保通过协调损失来保留美学品质。特征图$f_i$通过预训练的VGG-19网络的$i\in [1,6,11,18,25]$层提取而出，损失可以被计算为：
$${\mathcal{L}}_h=\sum _i{W}_2(f_i(Q),f_i(I^s))$$
令$P_1,P_2$分别为${\mathbb{R}}^n$上具有${\mu }_1,{\mu }_2\in {\mathbb{R}}^n$的平均值、非奇异协方差矩阵$C_1,C_2\in {\mathbb{R}}^{n\times n}$。$L^2$-Wasserstein距离$W_2(P_1,P_2)$可以被定义为：
$$A=\text{trace}(C_1+C_2-2(\sqrt{C_1}{C}_2\sqrt{C_1}{)}^{\frac{1}{2}})$$
$$W_2(P_1,P_2)=\sqrt{||{\mu }_1-{\mu }_2|{|}^2+A}$$
协调损失的集成确保优化的输出不仅满足功能要求，而且保留美学品质。本质上，SELR模块利用标记、编码、协调损失来优化生成的QR码的可扫描性和美观性。