目录
一、主要内容:
二、代码运行效果:
三、Weibull分布与风机风速:
四、Beta分布与光伏辐照度:
五、Normal分布与电负荷:
六、K-means聚类算法:
七、完整代码+数据下载:
一、主要内容:
本代码于Matlab平台构建,基于蒙特卡洛与K-means聚类方法,提出了一种用于风、光、负荷场景生成与削减技术,实现了随机变量典型场景的精确刻画。风电场景生成采用了Weibull分布函数,光伏场景生成采用了Beta分布,电负荷场景生成则采用了Normal分布。通过对风速、光照和负荷进行模拟,生成了考虑各能量随机波动特征的场景数据。随后,采用K-means算法对生成的场景数据进行聚类和削减,得到了精确的典型场景,从而提高场景数据的可管理性和可用性,为电力系统运行与分析提供了切实的参考。
本代码内容详细,注释丰富,出图美观,适合初学者模仿学习
二、代码运行效果:

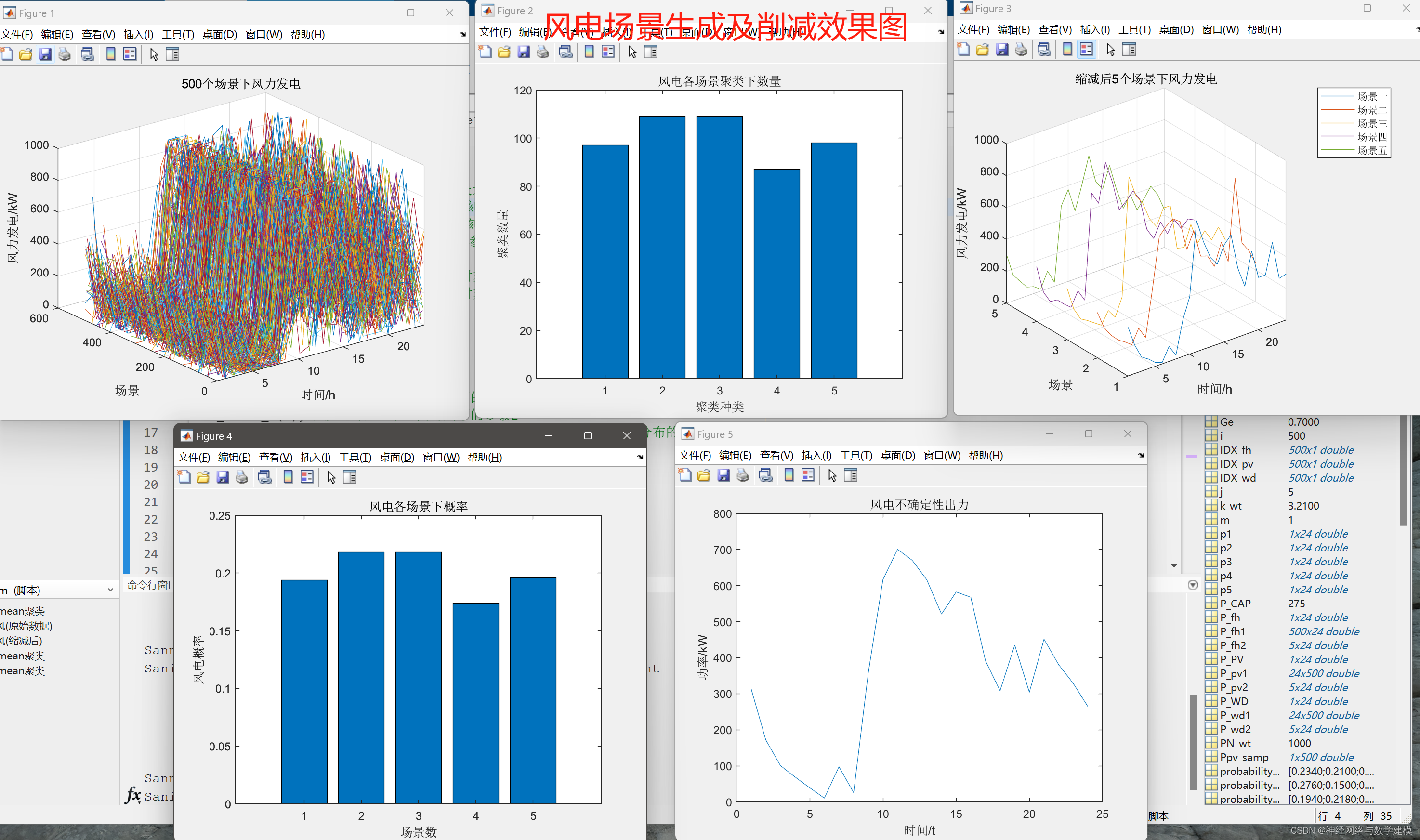
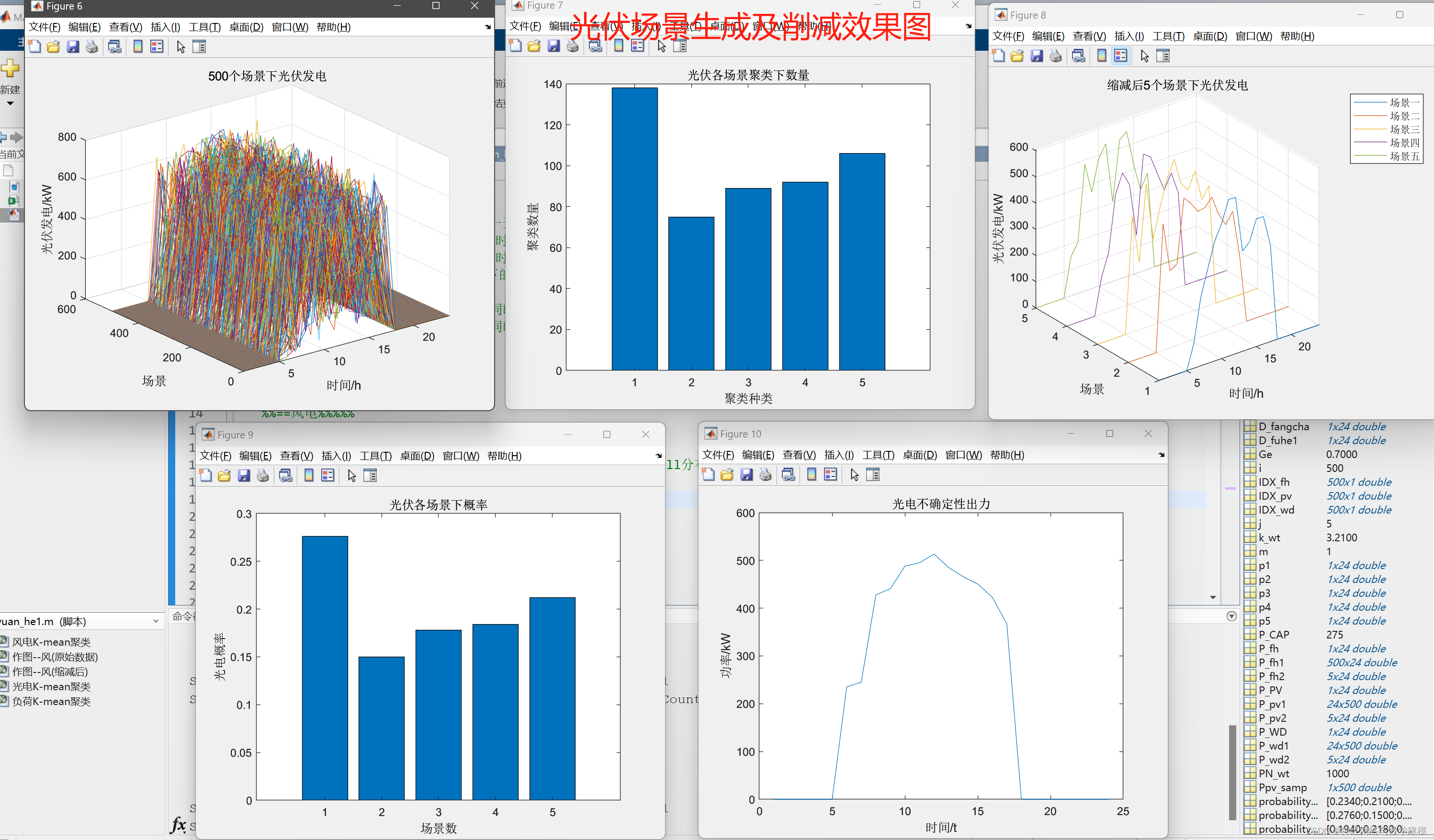
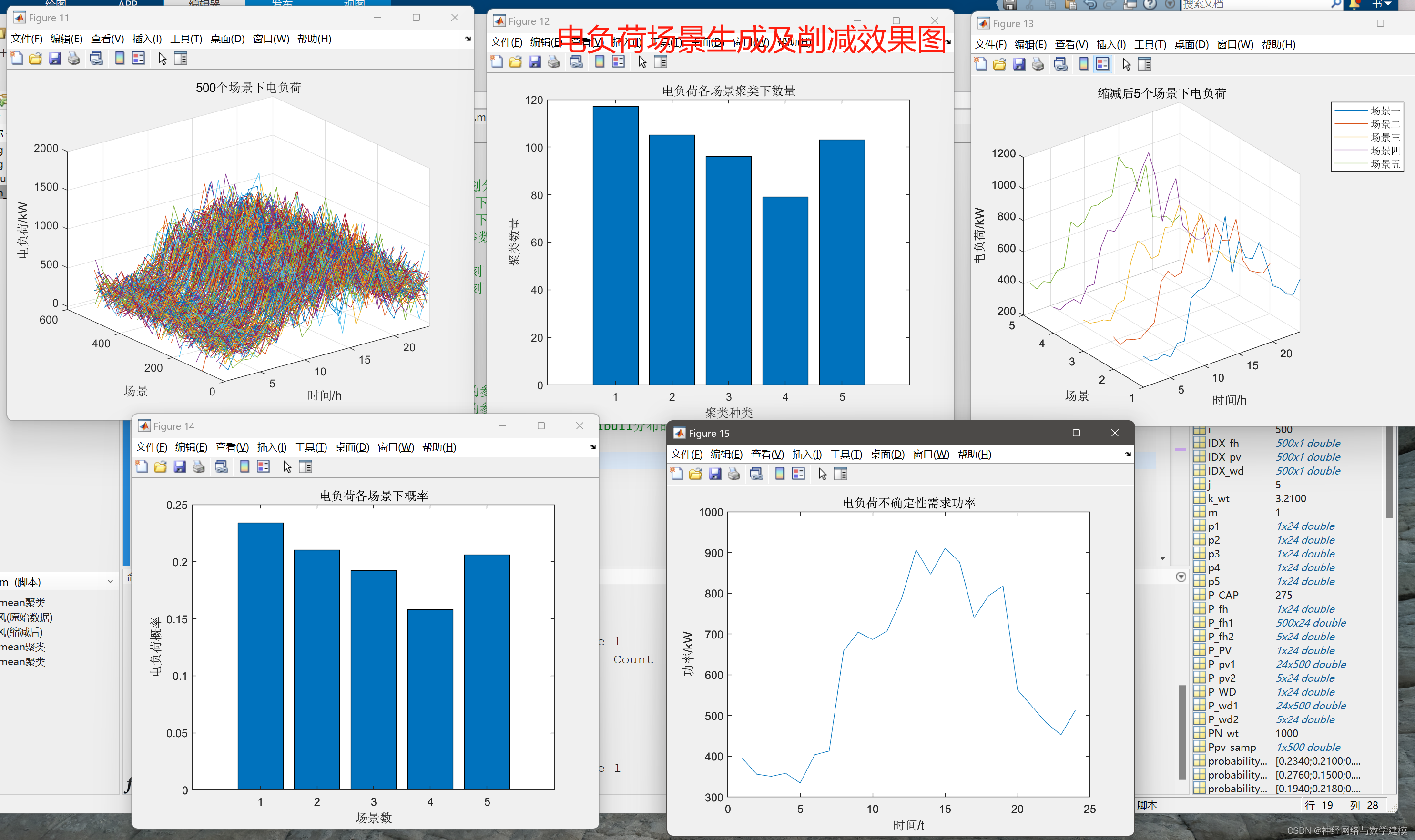
三、Weibull分布与风机风速:
韦伯分布(Weibull distribution)是一种常用的概率分布,常用于描述可靠性分析和寿命检验中的随机变量。它的概率密度函数为:

其中,λ 是尺度参数,决定了分布的尺度,k是形状参数,决定了分布的形状。
风速服从韦伯分布的假设是基于实际观测和经验的。虽然风速的分布可能受到多种因素的影响,但在许多情况下,韦伯分布能够相对准确地描述风速的分布情况。这可能是因为风速受到各种复杂因素的影响,包括地形、气候、季节等,而韦伯分布具有较强的灵活性,可以适应不同的数据分布情况。此外,韦伯分布具有数学上的便利性,其概率密度函数形式相对简单,易于计算和理解。这使得使用韦伯分布进行风速不确定性建模更加方便和高效。
四、Beta分布与光伏辐照度:
Beta分布是一个定义在有限区间内的连续概率分布,其概率密度函数形式为:

其中,x是定义在0-1上的随机变量,α和 β是分布的两个形状参数,B(α,β) 是Beta函数,用来保证概率密度函数的积分等于1。Beta分布常被用于描述随机变量在有限区间内的概率分布,特别是用于描述比例、概率等随机变量。
与光伏辐照度的关系是因为光伏辐照度(即太阳光照强度)通常被认为是一个介于0到1之间的比例值或概率值,因此可以将其分布建模为Beta分布。通过对光伏辐照度数据进行分析,可以使用Beta分布来估计不同辐照度水平下的概率密度函数,从而了解光伏辐照度的分布规律和特征,为光伏发电系统的设计和运行提供支持。
五、Normal分布与电负荷:
正态分布(Normal),也称为高斯分布,是统计学中最重要的分布之一,它具有钟型曲线的特征。正态分布的概率密度函数为:

其中,μ是均值,σ^2是方差,决定了分布的中心位置和形状。正态分布常用于描述许多自然现象和社会现象,例如身高、体重、温度等连续型随机变量。它具有许多重要的性质,例如68-95-99.7法则,即在正态分布中,大约68%的数据落在均值的一个标准差范围内,约95%的数据落在两个标准差范围内,约99.7%的数据落在三个标准差范围内。
中心极限定理指出,当随机变量的数量足够大时,其平均值的分布趋近于正态分布,无论原始分布是什么样的。在电力系统中,电负荷涉及到大量的用户和设备,因此根据中心极限定理,电负荷的总体波动性往往可以近似地服从正态分布。
六、K-means聚类算法:
K-means聚类算法是一种常用的无监督学习算法,用于将数据集分成K个不同的组或簇。其基本思想是通过迭代的方式,将数据点划分到K个簇中,使得每个数据点都属于距离最近的簇的中心点,同时最小化簇内数据点的平方误差和。以下是K-means聚类算法的基本步骤:
-
初始化: 随机选择K个初始聚类中心点,可以是数据集中的随机点或者通过其他方法选择。
-
聚类分配: 将数据集中的每个数据点分配到距离其最近的聚类中心所对应的簇中。
-
更新聚类中心: 对每个簇,重新计算其聚类中心,即计算簇内所有数据点的均值作为新的聚类中心。
-
重复步骤2和步骤3: 重复执行步骤2和步骤3,直到聚类中心不再发生变化或达到预定的迭代次数。
-
收敛: 当聚类中心不再发生变化时,算法收敛,得到最终的聚类结果。
七、完整代码+数据下载:






![洛谷P1000超级玛丽游戏题解[Python, Rust, Go]](https://img-blog.csdnimg.cn/direct/cd835ec5e9f541f2a262b47c1625392f.png)