大数据、物联网和人工智能等技术的进步揭示了传统冯·诺依曼的瓶颈架构,导致高能耗和有限的内存带宽。内存计算(IMC通过直接在内存中进行计算,提高了能效,提供了一个有前景的解决方案计算。现有的基于时域(TD)的IMC计算要么需要通过连续读/写方法进行多个周期的计算,要么通过以下方式增加了外围电路的复杂性采用累积延迟方法。
在本文中,我们提出了一种利用自旋的新型阵列结构转移力矩磁性随机存取存储器(STT-MRAM)位单元,减轻源极退化问题。通过利用这一先进技术并采用TD计算方案,我们成功地实现了各种算术运算,以及一组全面的布尔逻辑运算。
1.简介
现代计算机通过每天有效地处理大量数据,在人类社会的发展中发挥了关键作用。这些计算机依赖于被广泛认可的vonNeumann计算机体系结构,这是它们执行每一项操作的基础。在von Neumann体系结构中,可以追溯到20世纪40年代,计算/逻辑和存储单元被隔离并通过顺序传输指令的总线连接处理器和存储器之间的代码和计算数据。
然而,在存储器和处理器之间传输数据所需的能量和时间耗尽了我们计算机的有限极限,从而降低了现代计算系统的性能。这一挑战通常被认为是“冯-诺依曼瓶颈”或“记忆墙”。应对这一挑战需要使处理器和内存单元更接近。
这种策略与人脑处理信息的方式相当,在人脑中,计算和记忆之间没有物理区别,信息在记忆中处理。它可以减少数据传输,从而提高能效。非易失性存储器技术的出现,如电阻随机存取存储器(ReRAM)、相变存储器(PCM)、STT-MRAM等,为通过直接在数据位置进行计算来克服这一存储器障碍开辟了可能性。
在本文中,我们利用STT-MRAM[15-18]进行数据存储布尔算术运算由于其与互补金属氧化物半导体(CMOS)的兼容性和几个优点,包括高密度、低功耗和良好的耐久性。计算是通过基于时间的传感(TBS)实现的,与其他传感方法相比,TBS具有几个优势,包括鲁棒性、能效和高性能。在里面虽然在不同的内存内逻辑应用中探索TBS的工作有限,但我们提出的方法建立在最近基于时域计算的架构工作[23]的基础上,这是一个基线。然而,早期的工作遇到了几个问题,例如利用更多周期和增加的存储器位单元数量的连续读写操作,进一步加剧了vonNeumann问题,源极退化,由于级联延迟方法,需要两个感测放大器(SA)来执行两位操作,以及将输入进位表示为全加器(FA)实现的延迟,这引入了波动性。所提出的设计通过以替代方式采用翻转位单元来克服这些挑战。根据提出的想法,我们的第一步是实现输入布尔逻辑函数,主要是AND、OR和XOR,以及它们的补码。此外,该思想得到了扩展,并进行了深入分析。

图1
2.工作背景和动机本节解释了STT-MRAM位单元(1 T-1MTJ(磁性隧道结))和基于时间的感测放大器(TBSA)以及其他外围设备集成到IMC中的过程架构,强调整体系统设计。关于IMC结构的进一步细节,以及对阵列中的写入和读取操作的全面解释,在补充信息的第2节中提供。随后,本节讨论了与最近现有阵列相关的问题,清楚地展示了这项工作的动机。最后,提出了所提出的阵列,强调了其相对于现有阵列的优势。
考虑到传统的内存阵列仅限于支持,在读写操作中,逻辑基元的集成需要对传统阵列进行某些改进。这些增强可能涉及修改阵列结构、外围电路或两者的组合。通过这样的修改,存储器阵列获得了在执行其标准读取和写入操作的同时执行逻辑基元的能力。因此,在本文中,我们解决现有阵列架构通过对阵列结构进行必要的修改而带来的挑战(见图1a和b)。现有的阵列架构如图所示。面临几个挑战。首先,由于列写入能力有限,它对双SA的依赖阻碍了有效的两位操作,需要连续的写入操作来形成所需的组合。
在本节中,使用所提出的阵列实现了各种布尔逻辑基元,包括AND/NAND、OR/NOR和XOR/XNOR。补充信息第3节介绍了详细的设计和电路操作,以及瞬态仿真图。随后,工作范围扩展到3输入算术和逻辑电路,这些电路被实现为这些布尔运算的序列。为计算算术和逻辑功能而提出的体系结构如图所示。2,需要一种独特的设计方法。值得注意的是,FL和RL的配置对于交替的比特单元是反转的。这种改变确保了双向电流不用于将“0”或“1”写入MTJ,有效地缓解了通常被称为“源代码退化”的不平衡写入问题。

图2
MTJ具有FL-OL-RL结构,其中RL连接到存取晶体管。要写入“0”,电流从BL流到SL。相反,下一行采用RL-OL-FL结构,使“1”的写入与从BL流至SL的电流相结合。这种模式使“0”和“1”交替写入MTJ成为可能,这得益于WL/BL/SL驱动器和相关的写入电路。所提出的阵列在两种不同的模式下工作:内存模式和计算模式。在内存模式下,通过读取和写入操作从单比特单元存储和检索数据。相反,在计算模式中,执行不同的操作。
3.1. TD-IMC三输入算术逻辑电路的设计与开发
使用特定的逻辑基元在存储器内合成算术电路,然后将其映射到存储器阵列上用于存储器内实现。诸如FA和FS之类的操作的实现涉及三个操作数:A、B和进位. 通过引入额外的CMOS电路来解决FA实现所必需的问题。此电路设计用于容纳与操作数的值0和1相关的特定延迟。然而,它带来了各种挑战,如波动性、面积增加和功耗增强。为了解决这些问题,我们提出了一种解决方案,其中操作数被存储在所提出的阵列中的MTJ内。
通过这样做,该设计总共需要6个MTJ来容纳3个操作数的所有可能组合。值得注意的是,对于任何特定的组合,在任何给定时刻只有3个MTJ积极参与。因此,所提出的方法有效地解决了由附加电路的固有波动性引起的挑战。通过采用在交替行中交替MTJ的FL和RL的技术,我们消除了对多个TBSA的需要。相反,一个TBSA就足以实现所有所需的功能。除了算术运算之外,这些包括3输入逻辑门,例如AND/NAND、OR/NOR以及XOR/XNOR。
这里,多数函数(MAJ)被实现为直接计算进位FA操作。通过利用逻辑门函数并将它们的输出作为输入连接到MUX(M1,M2),现在实现了FA和FS。该过程举例说明了中间逻辑函数的有效利用,以便于以连贯的方式实现算术功能。算术加法器的控制布尔方程,描述SUM函数。
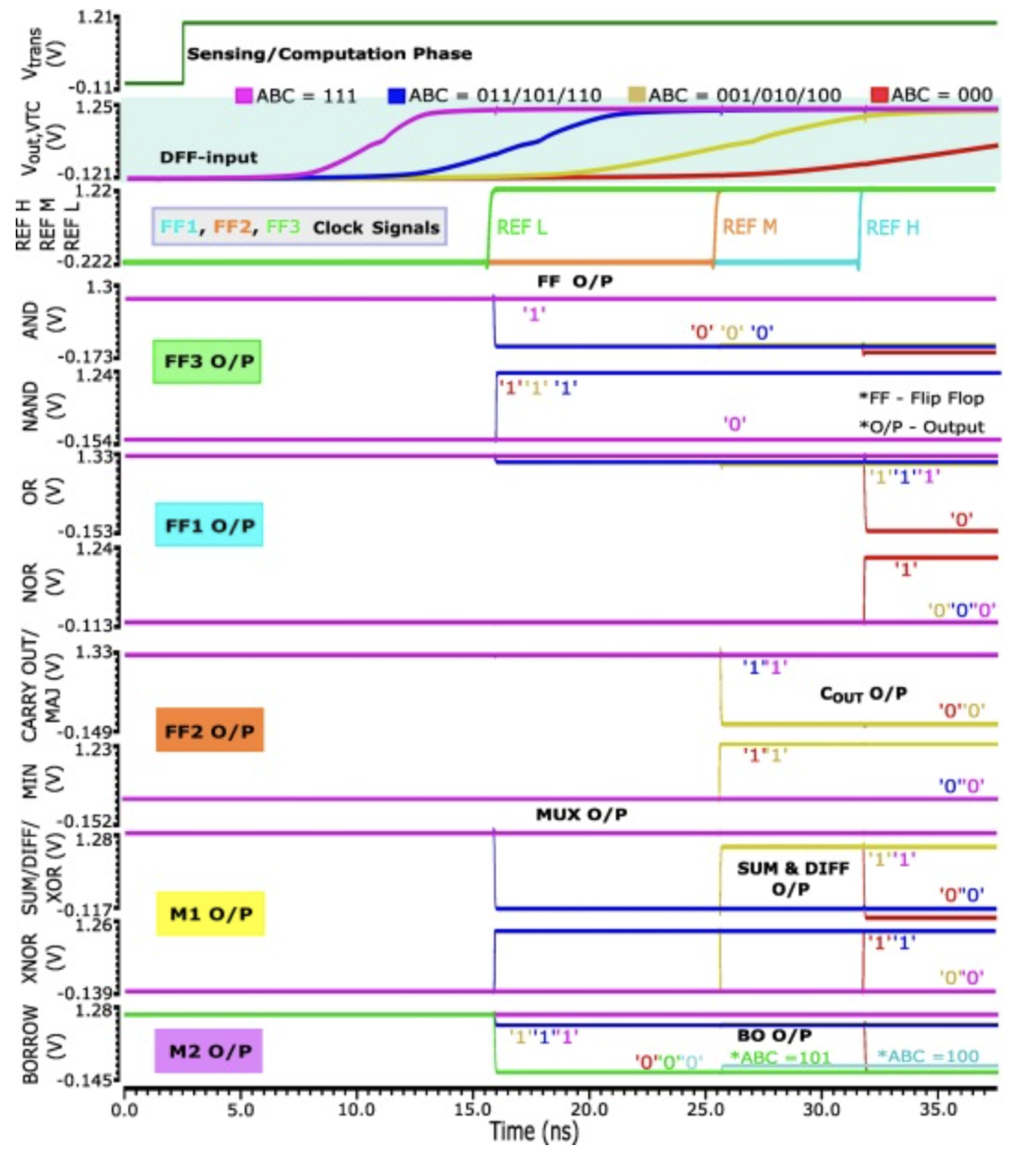
图3
电路工作关于全面的可视化表示,展示了包含所有功能实现的示意图。如图所示,字线WL用作操作数A、B,通过WL驱动器选择性激活以覆盖所有八个潜在组合。电路工作原理与2输入操作的说明相同。图3描述了算术和逻辑函数的瞬态模拟。由于有三个MTJ处于活动状态进一步减少与2输入操作相比,导致更长的延迟。
检查算术加法器、减法器和所有基本逻辑门功能的瞬态行为。使用各种颜色代码突出显示不同输入组合的输出:红色表示000,黄色表示001/010/100,蓝色表示011/101/110,粉色表示111。Borrow输出的操作与其他功能略有不同,它用六种不同的颜色表示,涵盖了所有八种输入组合:红色000、黄色001/010、浅蓝色100、蓝色011、绿色101/110和粉色111。
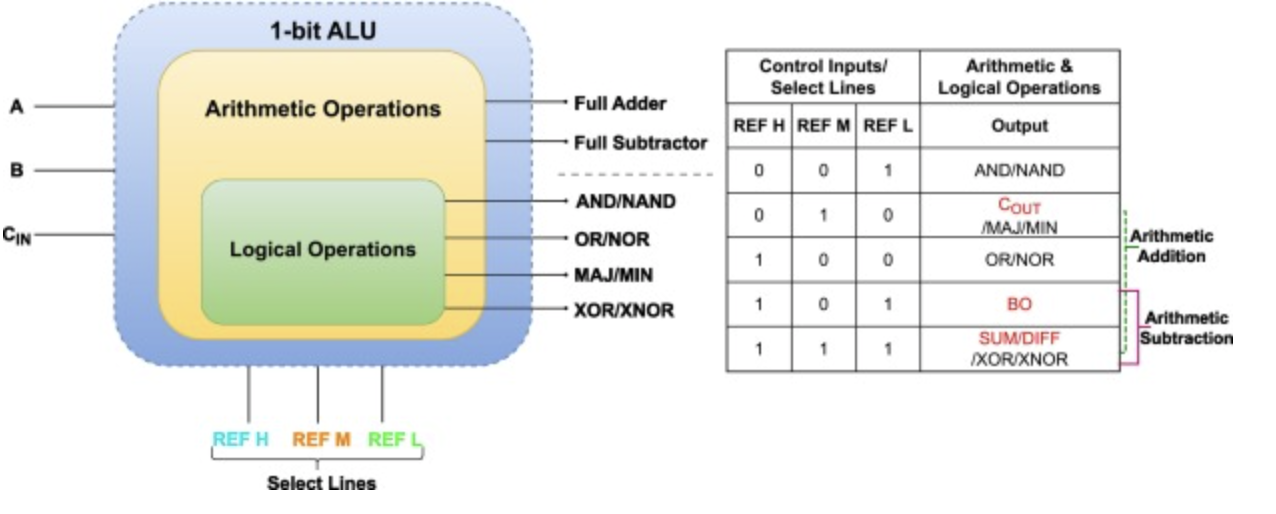
图4
根据前面的解释,很明显,图4所示的示意图被设计用于执行逻辑运算和算术运算。这意味着它起到1位ALU的作用,如图4所示。信号REF H、REF M和REF L本身起到控制输入或选择线的作用,它们规定并指导算术和逻辑运算的执行。这些信号的特定组合或状态决定ALU将对输入数据执行的操作。通过操纵这些信号,ALU可以被配置为执行各种任务,例如算术加法、算术减法、逐位逻辑运算等等。随着任务变得更加复杂和数据量的扩大,ALU形成了处理器的主干,使它们能够快速高效地处理复杂的计算[31,32]。
参考来源:
[1] https://bbs.csdn.net/topics/618238711
[2] https://bbs.csdn.net/topics/618242271