AdaBoost算法详解自用笔记(1)二分类问题举例分析
提升方法的思路
AdaBoost作为一种提升方法,其需要回答两个问题:一是每一轮如何改变训练数据的权重或概率分布;二是如何将弱分类器组合成一个强分类器。对于第一个问题,AdaBoost的做法是提高那些被前一轮弱分类器错误分类样本的权重,而降低那些被正确分类样本的权重,这样一来那些没有得到正确分类的数据,由于权重被增大后,将在下一轮的弱分类器中被给予更大关注。对于第二个问题,AdaBoost的做法是采取多数表决的方式,加大分类误差率小的弱分类器的权重,减小分类误差率大的弱分类器的权重,这样一来使得分类误差率小的弱分类器将会在表决中起到更大的作用。

以一道例题讲解算法过程
以下面的表格为例,自变量
X
X
X是一维的离散数据,取值从0到9,
Y
Y
Y是二分类因变量,取值是1或-1。这里通过这么一道简单的例题过一遍AdaBoost的算法过程,而不直接推理证明公式,让大家对其有个直观的理解。
N
N
N代表样本总数,值为10;
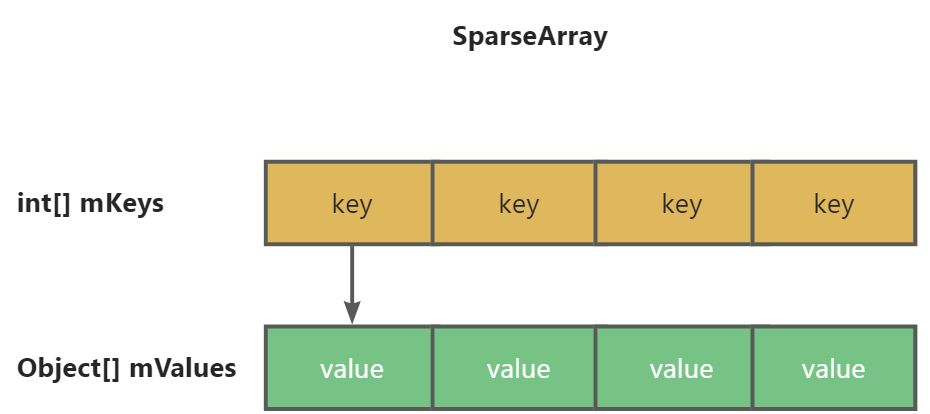
ω
m
,
i
\omega_m,_i
ωm,i代表第
m
m
m轮弱分类器第
i
i
i个样本的权重;
D
m
D_m
Dm代表第
m
m
m轮的权重集合;
y
^
\hat{y}
y^代表预测值。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
| 弱分类器1的 y ^ \hat{y} y^ | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 弱分类器2的 y ^ \hat{y} y^ | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
Step1 初始化数据权重
从上面的表格我们可以知道,共有10个样本,因此每一个样本的权重初始化为:
ω
1
,
1
=
ω
1
,
2
=
⋅
⋅
⋅
=
ω
1
,
10
=
1
N
=
1
10
\omega_{1,1}=\omega_{1,2}=\cdot\cdot\cdot=\omega_{1,10}=\frac{1}{N}=\frac{1}{10}
ω1,1=ω1,2=⋅⋅⋅=ω1,10=N1=101
因此对应的初始权重可以写成集合为:
D 1 = { ω 1 , 1 , ω 1 , 2 ⋅ ⋅ ⋅ ω 1 , 10 } D_1=\left\{\begin{matrix} \omega_{1,1},\omega_{1,2}\cdot\cdot\cdot\omega_{1,10} \end{matrix}\right\} D1={ω1,1,ω1,2⋅⋅⋅ω1,10}
Step2 第一轮学习器的选择
对于上面10个样本的情况,有9种切分方法(以
X
=
2.5
X=2.5
X=2.5和
X
=
2.6
X=2.6
X=2.6作为阈值的切分效果是一样的),每一种切分方法都对应了一种弱分类器。对于弱分类器1而言,误判的个数有3个,分别是序号7、8、9对应的样本;对于弱分类器2而言,误判的个数有6个,分别是序号4、5、6、7、8、9对应的样本。
那么我们如何评估哪一个弱分类器效果更好呢?这里引入误分类率
e
m
e_m
em这个概念,其不仅关注误判的个数,还关注数据的权重。其中,第
m
m
m轮学习器(这一轮最好的弱分类器和往轮的学习器组成这一轮的学习器,对于第一轮而言,最好的弱分类器就是学习器)的误分类率计算如下:
e
m
=
∑
i
=
1
N
ω
m
,
i
I
(
P
(
G
1
(
x
i
)
≠
y
i
)
)
e_m=\sum_{i=1}^{N}\omega_{m,i}I(P(G_1(x_i)\neq y_i))
em=i=1∑Nωm,iI(P(G1(xi)=yi))
由于计算针对的是一轮而不是一个样本,那么要将当前轮的所有样本的误分类率累加求和。引入示性函数
I
I
I告诉我们误分类率关注的是错误分类的部分,因此在计算的时候以及权重更新的时候,不用去关注正确分类的部分,因为示性函数将这一部分赋值为0。其中,示性函数定义如下:
I
(
P
(
G
1
(
x
i
)
≠
y
i
)
=
{
1
,
G
1
(
x
i
)
≠
y
i
0
,
G
1
(
x
i
)
=
y
i
I(P(G_1(x_i)\neq y_i)= \begin{cases} 1,G_1(x_i)\neq y_i\\ 0,G_1(x_i)=y_i \end{cases}
I(P(G1(xi)=yi)={1,G1(xi)=yi0,G1(xi)=yi
第一轮中,我们在
D
1
D_1
D1的权重下进行9种弱分类器误分类率的计算,对于弱分类器1而言,误分类率计算如下:
3
×
1
10
×
1
=
0.3
3\times\frac{1}{10}\times1=0.3
3×101×1=0.3
对于弱分类器2而言,误分类率计算如下:
6
×
1
10
×
1
=
0.6
6\times\frac{1}{10}\times1=0.6
6×101×1=0.6
以此类推计算剩下的7种切分方式,发现弱分类器1的误分类率最低,因此我们选择弱分类器1作为第一轮的分类器学习器,我们把它记为:
G
1
=
{
+
1
,
x
<
2.5
−
1
,
x
>
2.5
G_1=\begin{cases} +1,x<2.5\\ -1,x>2.5 \end{cases}
G1={+1,x<2.5−1,x>2.5
对应的误分类率为:
e
1
=
P
(
G
1
(
x
i
)
≠
y
i
)
=
0.3
e_1=P(G_1(x_i)\neq y_i)=0.3
e1=P(G1(xi)=yi)=0.3
在选择了第一轮的学习器后,现在我们要为第二轮的选择进行权重更新,使得第二轮组合成的新学习器效果优于第一轮的学习器。对于第二轮的数据权重,其计算公式如下:
ω
2
,
i
=
ω
1
,
i
Z
1
exp
(
−
α
1
y
i
G
1
(
x
i
)
)
\omega_{2,i}=\frac{\omega_{1,i}}{Z_1}\exp(-\alpha_1y_iG_1(x_i))
ω2,i=Z1ω1,iexp(−α1yiG1(xi))
其中,
Z
1
Z_1
Z1是规范化因子。通俗地讲,是将更新后的权重之和归为 1,保证权重序列以一个离散的概率分布出现(后面章节再进行详细推导)。其计算公式如下:
Z
1
=
ω
1
,
i
exp
(
−
α
1
y
i
G
1
(
x
1
)
)
Z_1=\omega_{1,i}\exp(-\alpha_1y_iG_1(x_1))
Z1=ω1,iexp(−α1yiG1(x1))
而
α
i
\alpha_i
αi是转换系数,它与误分类率之间有一个公式(如何推导出来的也在后面章节会详细说明)。其中,弱分类器1的转换系数为:
α
1
=
1
2
l
n
1
−
e
1
e
1
=
0.4236
\alpha_1=\frac{1}{2}ln\frac{1-e_1}{e_1}=0.4236
α1=21lne11−e1=0.4236
在上面三条公式中,
y
i
y_i
yi和
G
1
(
x
i
)
G_1(x_i)
G1(xi)分别代表第
i
i
i个样本的真实值和第一轮学习器第
i
i
i个样本的预测值。如果真实值和预测值相同,即预测正确,那么
(
−
α
1
y
i
G
1
(
x
1
)
)
(-\alpha_1y_iG_1(x_1))
(−α1yiG1(x1))即为
−
α
1
-\alpha_1
−α1,如果预测错误,那么
(
−
α
1
y
i
G
1
(
x
1
)
)
(-\alpha_1y_iG_1(x_1))
(−α1yiG1(x1))即为
α
1
\alpha_1
α1。经过计算,第二轮的数据权重集合为:
D
2
=
{
0.07143
,
0.07143
,
0.07143
,
0.07143
,
0.07143
,
0.07143
,
0.16667
,
0.16667
,
0.16667
,
0.16667
}
D_2=\left\{\begin{matrix} 0.07143,0.07143,0.07143,0.07143,0.07143,0.07143,0.16667,0.16667,0.16667,0.16667 \end{matrix}\right\}
D2={0.07143,0.07143,0.07143,0.07143,0.07143,0.07143,0.16667,0.16667,0.16667,0.16667}
由上述公式可知,分类正确的数据权重从0.1下降到了0.07143,而分类错误的数据权重从0.1提升到了0.16667。此时,第一轮的决策函数可写为:
f
1
(
x
)
=
α
1
G
1
(
x
)
f_1(x)=\alpha_1G_1(x)
f1(x)=α1G1(x)
第一轮的学习器可写为:
s
i
g
n
[
f
1
(
x
)
]
sign[f_1(x)]
sign[f1(x)]
Step3 第二轮学习器的选择
仿照Step2,我们最佳弱分类器划分阈值为
X
=
8.5
X=8.5
X=8.5,因此我们把它作为第二轮的学习器,记为:
G
2
=
{
+
1
,
x
<
8.5
−
1
,
x
>
8.5
G_2=\begin{cases} +1,x<8.5\\ -1,x>8.5 \end{cases}
G2={+1,x<8.5−1,x>8.5
此时的误判样本即为序号为4,5,6对应的样本,在
D
2
D_2
D2的权重基础下,我们求得第二轮学习器的误分类率为:
e
2
=
∑
i
=
1
10
ω
2
,
i
I
(
P
(
G
2
(
x
i
)
≠
y
i
)
)
=
0.07143
×
1
+
0.07143
×
1
+
0.07143
×
1
=
0.2143
e_2=\sum_{i=1}^{10}\omega_{2,i}I(P(G_2(x_i)\neq y_i)) =0.07143\times1+0.07143\times1+0.07143\times1 =0.2143
e2=i=1∑10ω2,iI(P(G2(xi)=yi))=0.07143×1+0.07143×1+0.07143×1=0.2143
同理,第二轮所选学习器的转换系数计算如下:
α
2
=
1
2
l
n
1
−
e
2
e
2
=
1
2
l
n
1
−
0.2143
0.2143
=
0.6496
\alpha_2=\frac{1}{2}ln\frac{1-e_2}{e_2}=\frac{1}{2}ln\frac{1-0.2143}{0.2143}=0.6496
α2=21lne21−e2=21ln0.21431−0.2143=0.6496
此时,第二轮的决策函数可写为:
f
2
(
x
)
=
α
1
G
1
(
x
)
+
α
2
G
2
(
x
)
f_2(x)=\alpha_1G_1(x)+\alpha_2G_2(x)
f2(x)=α1G1(x)+α2G2(x)
相应的学习器为:
s
i
g
n
[
f
2
(
x
)
]
=
s
i
g
n
[
0.4236
G
1
(
x
)
+
0.6496
G
2
(
x
)
]
sign[f_2(x)]=sign[0.4236G_1(x)+0.6496G_2(x)]
sign[f2(x)]=sign[0.4236G1(x)+0.6496G2(x)]
这个时候分类的结果看的是
s
i
g
n
[
f
2
(
x
)
]
sign[f_2(x)]
sign[f2(x)],比如序号1对应的样本,
G
1
(
x
1
)
=
1
G_1(x_1)=1
G1(x1)=1,
G
2
(
x
1
)
=
1
G_2(x_1)=1
G2(x1)=1,对应的
s
i
g
n
[
f
2
(
x
)
]
=
s
g
i
n
[
0.4236
×
1
+
0.6469
×
1
=
1.0732
>
0
]
sign[f_2(x)]=sgin[0.4236\times1+0.6469\times1=1.0732>0]
sign[f2(x)]=sgin[0.4236×1+0.6469×1=1.0732>0],所以第二轮学习器将序号1这个样本分类为1。
Step4 第三轮学习器的选择
仿照Step2和Step3,我们首先更新数据权重,计算得到的第三轮的权重集合为:
D
3
=
{
0.0455
,
0.0455
,
0.0455
,
0.16667
,
0.16667
,
0.16667
,
0.1060
,
0.1060
,
0.1060
,
0.0455
}
D_3=\left\{\begin{matrix} 0.0455,0.0455,0.0455,0.16667,0.16667,0.16667,0.1060,0.1060,0.1060,0.0455 \end{matrix}\right\}
D3={0.0455,0.0455,0.0455,0.16667,0.16667,0.16667,0.1060,0.1060,0.1060,0.0455}
接着我们计算第三轮各个弱分类器的误分类率,最终发现阈值为
X
=
5.5
X=5.5
X=5.5的弱分类器误分类率最小,我们把其作为第三轮的学习器,记为:
G
3
=
{
+
1
,
x
<
5.5
−
1
,
x
>
5.5
G_3=\begin{cases} +1,x<5.5\\ -1,x>5.5 \end{cases}
G3={+1,x<5.5−1,x>5.5
其分类错误的是序号为1,2,3,10对应的样本,那么我们可以计算出第三轮学习器的误分类率为:
e
3
=
∑
i
=
1
10
ω
3
,
i
I
(
P
(
G
3
(
x
i
)
≠
y
i
)
)
=
0.0455
×
1
+
0.0455
×
1
+
0.0455
×
1
+
0.0455
×
1
=
0.1820
e_3=\sum_{i=1}^{10}\omega_{3,i}I(P(G_3(x_i)\neq y_i)) =0.0455\times1+0.0455\times1+0.0455\times1+0.0455\times1 =0.1820
e3=i=1∑10ω3,iI(P(G3(xi)=yi))=0.0455×1+0.0455×1+0.0455×1+0.0455×1=0.1820
最后我们计算第三轮所选的学习器的转换系数:
α
3
=
1
2
l
n
1
−
e
3
e
3
=
1
2
l
n
1
−
0.1820
0.1820
=
0.7514
\alpha_3=\frac{1}{2}ln\frac{1-e_3}{e_3}=\frac{1}{2}ln\frac{1-0.1820}{0.1820}=0.7514
α3=21lne31−e3=21ln0.18201−0.1820=0.7514
此时,到第三轮这里生成的决策函数就变成了:
f
3
(
x
)
=
α
1
G
1
(
x
)
+
α
2
G
2
(
x
)
+
α
3
G
3
(
x
)
f_3(x)=\alpha_1G_1(x)+\alpha_2G_2(x)+\alpha_3G_3(x)
f3(x)=α1G1(x)+α2G2(x)+α3G3(x)
相应的学习器为:
s
i
g
n
[
f
3
(
x
)
]
=
s
i
g
n
[
0.4236
G
1
(
x
)
+
0.6496
G
2
(
x
)
+
0.7514
G
3
(
x
3
)
]
sign[f_3(x)]=sign[0.4236G_1(x)+0.6496G_2(x)+0.7514G_3(x_3)]
sign[f3(x)]=sign[0.4236G1(x)+0.6496G2(x)+0.7514G3(x3)]
经过了这三轮选择的学习器的叠加,此时的强学习器所预测的准确率达到了100%,自此大功告成!
参考知乎文章【十分钟 机器学习 系列课程】 讲义(55):AdaBoost例题讲解 - 知乎 (zhihu.com)以及李航《统计学习方法》