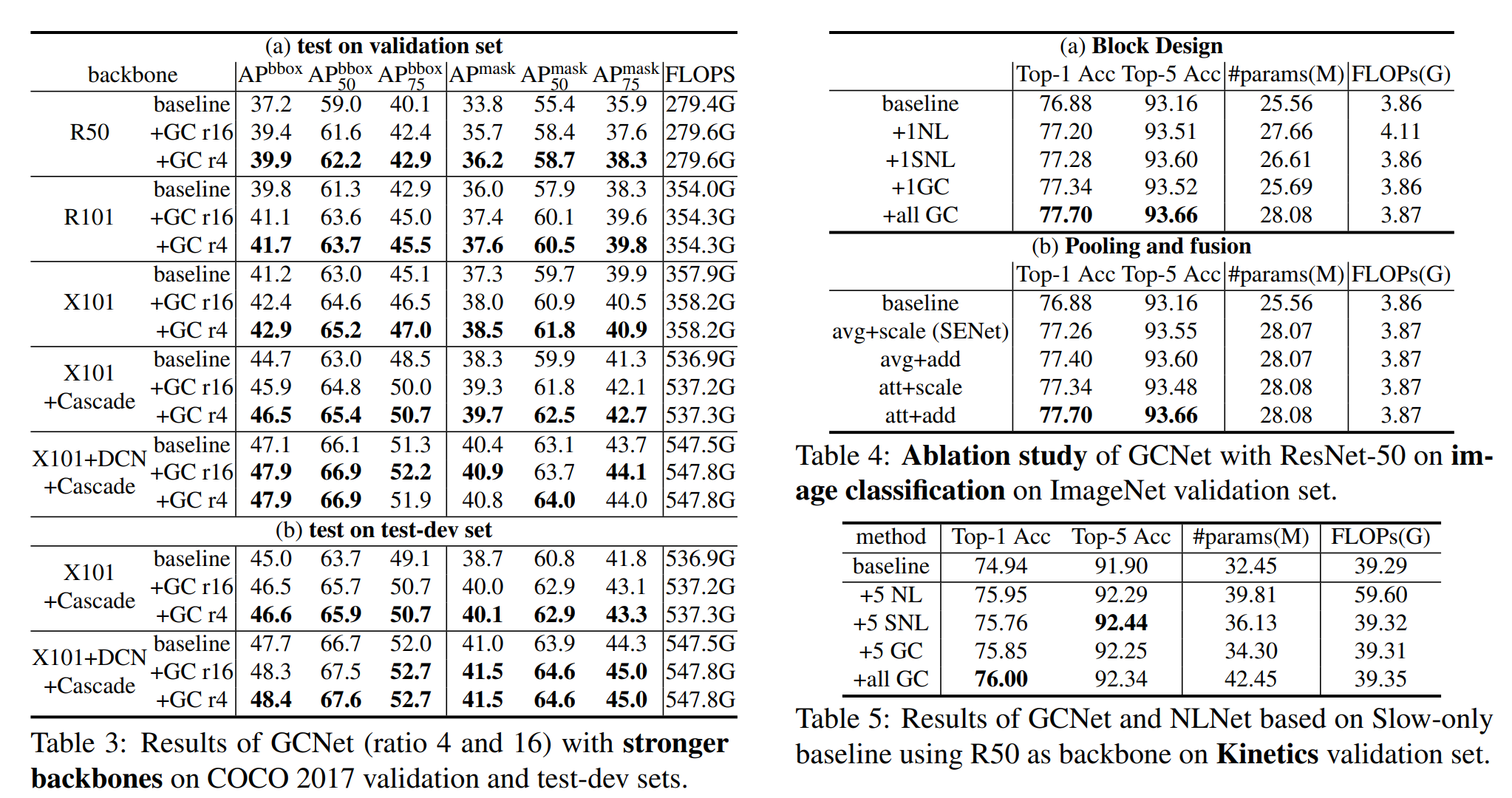
4、索引取值
像对 python 列表那样进行切片,对 NumPy 数组进行任意的索引和切片,取得数组或者单个的元素值。
arr1=np.array([1,2,3,4,5,6,7])
print(arr1)
print(arr1[5])
print(arr1[2:4])
输出:[1 2 3 4 5 6 7]
6
[3 4]
B = np.array([[5, 6,6], [7, 8,9]])
print(B)
print(B[1,1])
输出:array([[5, 6, 6],
[7, 8, 9]])
B[1,1]
B = np.array([[3,4,5, 6], [ 8,9,10,11]])
print(B)
print(B[1,1])
print(B[0,1:3])
print(B[0:2,1:3])
输出:
[[ 3 4 5 6]
[ 8 9 10 11]]
9
[4 5]
[[ 4 5]
[ 9 10]]
5、聚合功能
NumPy模块中还提供聚合功能函数,主要包括 min、max 和 sum、 mean 等,还可以使用 prod 得到所有元素的乘积(也可以使用参数axis=1计算每一行元素的乘积。),使用 std 得到标准差等。
例如:
arr1=np.array([1,2,3])
arr2=np.array([[1,10],[100,1000],[10000,100000]])
arr3=np.array([1,2])
print(arr2)
print('最大值是:',arr2.max())
print( '最小值是:', arr2.min())
print('平均值是:', arr2.mean())
print( '求和是:', arr2.sum())
print('arr1元素乘积是:', arr1.prod())
print('标准差是:',arr2.std())
输出:
[[ 1 10]
[ 100 1000]
[ 10000 100000]]
最大值是: 100000
最小值是: 1
平均值是: 18518.5
求和是: 111111
arr1元素乘积是: 6
标准差是: 36613.752078283374
6、矩阵运算
数组算术运算和矩阵运算的一个关键区别是矩阵乘法使用点乘,为每个矩阵赋予 dot() 方法,我们可以用它与其他矩阵执行点乘操作:
numpy.dot(a, b, out=None)
其中,a和b是要进行矩阵乘法运算的两个数组。这两个数组可以是一维或多维的,但是它们的维度必须满足矩阵乘法的规则。out参数是可选的,用于指定结果存储的位置。
矩阵相乘是np.dot函数最常用的功能之一。有两个矩阵A和B,它们的形状分别为(m, n)和(n, p),则它们的乘积C的形状为(m, p),即C = A.dot(B)。下面是一个例子:
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
C = np.dot(A, B)
print(C)
输出:
[[19 22]
[43 50]]
7、矩阵转置
处理矩阵时的一个常见需求是旋转矩阵。当需要对两个矩阵执行点乘运算并对齐它们共享的维度时,通常需要进行转置。NumPy 数组有一个方便的方法 T 来求得矩阵转置:
print(arr2)
print(arr2.T)
输出:
[[ 1 10]
[ 100 1000]
[ 10000 100000]]
转置后的矩阵
[[ 1 100 10000]
[ 10 1000 100000]]
8、均方差计算
均方差公式:
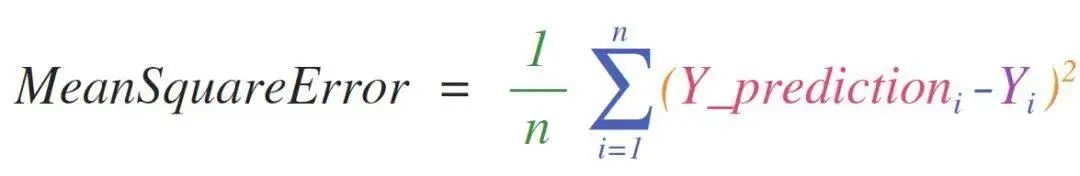
这个均方差公式,是监督机器学习模型处理回归问题的核心,是预测值和实际值之间的波动大小的情况的量化值。而在在 NumPy 中实现该公式就很容易了:

这样做的方法就是将predictions数组和实际原值labels数据的差平方,再求和并求平均,得到均方差error,结果即为该预测的误差值和模型质量评分。而在计算过程中不用在
这样做的好处在于,NumPy 并不关心 predictions 和 labels 包含一个值还是一千个值(只要它们大小相同)。
代码举例:
np.random.seed(0)
predictions=np.random.random(10)
labels =np.random.random(10)
print('预测值是:',predictions)
print('样本实验值是:', labels)
error=(1/10)*np.sum(np.square(predictions-labels))
print('均方差error=',error)
输出结果:
预测值是: [0.62027802 0.62348494 0.03833878 0.04591209 0.24930147 0.2025378
0.55266408 0.91764512 0.00142433 0.60320505]
样本实验值是: [0.18542253 0.36114737 0.93138771 0.9414958 0.86235216 0.91268468
0.65224417 0.69472437 0.16548572 0.3526313 ]
均方差error= 0.28869798046669465
先介绍到这里,如果知识有用,欢迎评论、收藏、点赞等,也欢迎学习的小伙伴交流。