---

前言

本文将介绍包络调制方法，该方法的思路是将$m(t)$作为已调信号的复包络的模——即包络。

---

一、AM的数学表示

根据包络调制的思路，我们有如下数学表达式：

$|s_L(t)|=|\left[s(t)+j\hat{s}(t)\right]e^{-j2\pi f_{c}t}|=m(t)$

这里我们为了简便假设随机相位$\varphi =0$。很快我们会发现一个问题，如果按照这种思路去调制，那不是必须要求$m(t)$始终大于零吗？对调制信号施加限制的调制方法显然是不够友好的。为了解决这个问题，我们可以使其叠加上一个直流信号，就可以了。因此我们重写上述表达式：

$|s_L(t)|=A_c+m(t)$

这个直流信号的幅值$A_c$只要满足$A_c⩾|m(t){|}_{\max }$即可。有了这个关系后，在接收端可以对已调信号求复包络再取模，即可获取原信号的信息。然而满足条件的$s_L(t)$可以有很多，简单而言最直接的做法就是取全正的那一个，即$s_L(t)=|s_L(t)|$，从而可以得到已调信号为：

$s(t)=(A_c+m(t))\cos 2\pi f_{c}t$

这就上包络调制信号的一般形式。(即使把个别$s_L(t)$值取为相反数，其对应的带通信号仍然可以携带原信号的信息，因为包络不变。但是一般没必要去这样刁难自己，就取最简单的方式即可。)

二、AM的相干解调

仔细观察AM信号与DSB-SC信号的差别，发现其实就是在原来DSB-SC信号的基础上，多发了一个载波信号$A_c\cos 2\pi f_{c}t$, 这样在接收端通过窄带滤波即可取出该载波，然后进行相干解调获得信号$A_c+m(t)$,最后再通过一个隔直流电路即可取出原信号$m(t)$

三、AM的非相干解调

如果AM调制只是为了多发了一个载波信号，那么就应该叫DSB调制，而不是载波调制。其之所以称之为包络调制，是因为可以通过包络检波的方式进行非相干解调。

所谓包络检波就是将包裹着信号波形的外围轮廓取出来，下图中虚线部分就是包络。（这里其实可以发现包络并不等于模值$|s(t)|$，而是其复包络的模值，当载波频率趋于无穷时，二者在图上会更为相似。这里可以进一步加深对包络与复包络的理解。）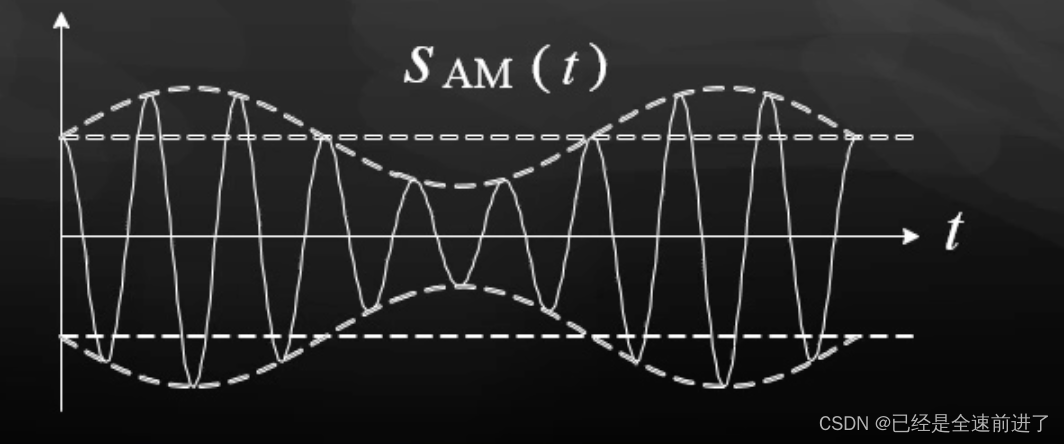

取出了包络$A_c+m(t)$，同样只需要再进行隔直流即可取出原信号。当然，包络调制还有一点区别于所谓DSB调制的地方在于，添加的载波信号的幅值$A_c$要满足之前所题的限制条件，使得$A_c+m(t)$确实能作为包络。

四、AM调制的性能

在带宽资源上同样占用了2W的带宽。

在信噪比上，隔直流之后仍然是$\frac{P_m}{2N_{0}W}$。

因为需要使用一部分功率发射载波信号，因此有了有效信号发射功率与总发射功率之比——调制效率的概念，此时调制效率为

$\eta =\frac{P_m}{P_m+A_c^2}$

此时可以看到，$A_c$取不同的值，会影响到调制的效率。让我们重新分析一下AM信号：

$s(t)=A_c(1+\frac{m(t)}{A_c})\cos 2\pi f_{c}t$
$=A_c(1+\frac{|m(t){|}_{\max }}{A_c}\cdot \frac{m(t)}{|m(t){|}_{\max }})\cos 2\pi f_{c}t$
进行一下变量替换$a=\frac{|m(t){|}_{\max }}{A_c}$,$m_n(t)=\frac{m(t)}{|m(t){|}_{\max }}$,得
$=A_c(1+a{m}_n(t))\cos 2\pi f_{c}t$

这就是AM信号的带调幅系数的表达形式，其中$a$称为调幅系数，根据$A_c$满足的条件易知$0<a⩽1$。$m_n(t)$为原信号的归一化信号。调幅系数越小，则说明发射的载波功率越大，也就会导致调制效率越低。

---

总结

本文介绍了从包络的角度去完成模拟信号的调制，从而可以不依赖于载波恢复来进行信号的解调。评价性能时需要注意调幅系数的概念理解以及其与调制效率的关系。