跟着博主一起刷题
这里使用的是题库：
https://leetcode.cn/problem-list/xb9nqhhg/?page=1

剑指 Offer 49. 丑数

剑指 Offer 49. 丑数
我一开始的思路是，把数字1~无穷的遍历，知道遍历n个丑数为止。那么怎么求一个数是不是丑数呢？丑数是只包含2，3，5的质因子，例如一个数位 2223355 我们先把2除完，再除完3，最后除完5看结果是不是1即可。代码：

private boolean isUgly(int n){
        if(n%2==0)return isUgly(n/2);
        if(n%3==0)return isUgly(n/3);
        if(n%5==0)return isUgly(n/5);
        return n==1;
    }

但是这种方法时间复杂度很高，结果就是时间超限了，我们得另寻方法。
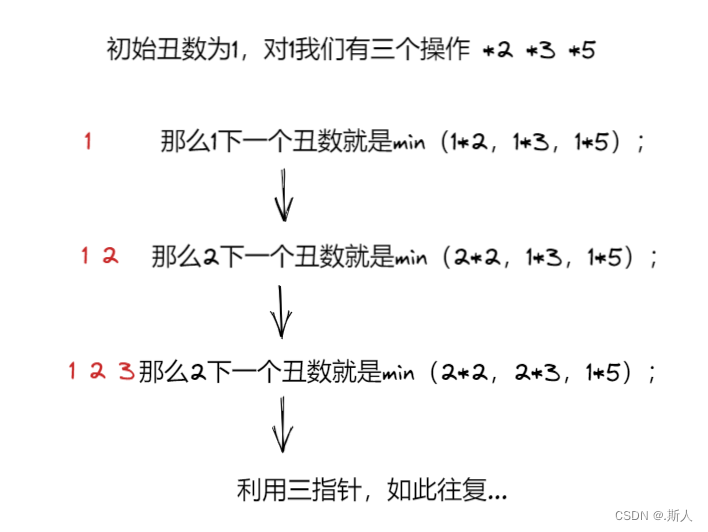
上面的方法时间超限是判断了很多不是丑数的数字，有没有方法可以让我们自己造丑数呢？有的！初始的丑数 2 3 ，3后面的丑数是什么呢？我们发现22<5，所以是2 3 4，那么4后面的丑数是什么？发现23的相邻最小的丑数。什么意思呢？**意思就是我们可以通过初始的丑数，来推出之后的最小的丑数。**具体做法：

class Solution {
    public int nthUglyNumber(int n) {
        int p2=0,p3=0,p5=0;
        int[] ugly=new int[n];
        ugly[0]=1;
        for(int i=1;i<n;i++){
            int n2=ugly[p2]*2;
            int n3=ugly[p3]*3;
            int n5=ugly[p5]*5;
            int min=Math.min(n2,Math.min(n3,n5));
            if(n2==min)p2++;
            if(n3==min)p3++;
            if(n5==min)p5++;
            ugly[i]=min;
        }
        return ugly[n-1];
    }
}

剑指 Offer 51. 数组中的逆序对

剑指 Offer 51. 数组中的逆序对
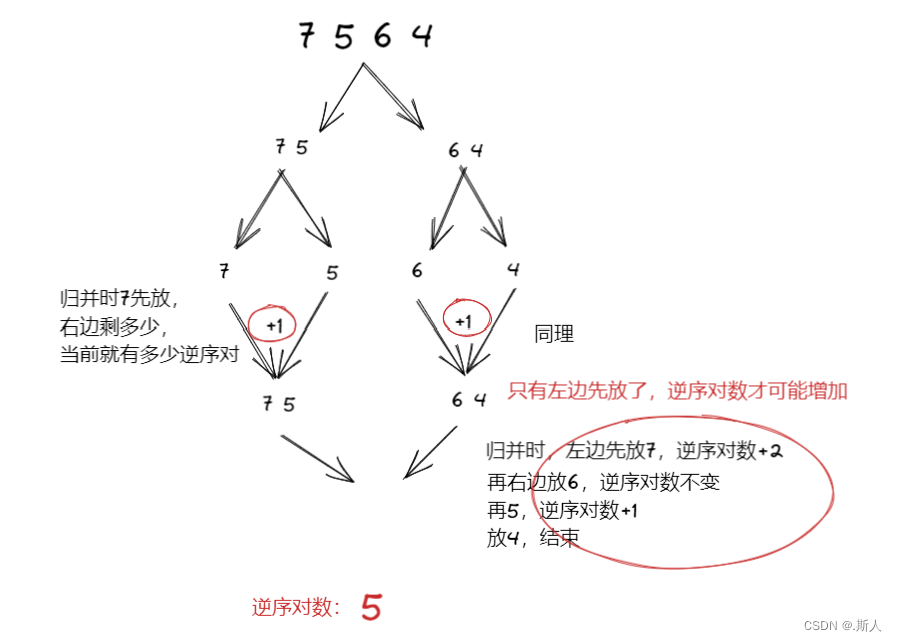
如果我们一个一个比较时间一定会超限，因为时间复杂度是O（N^2）。注意看：
利用归并排序的性质

class Solution {
    private int count=0;
    private int[] nums,tmp;
    public int reversePairs(int[] nums) {
        this.nums=nums;
        tmp=new int[nums.length];
        if(nums.length!=0){
            merge(0,nums.length);
        }
        return count;
    }

    private void merge(int left,int right){
        if(left>=right-1)return;
        int mid=(right-left)/2+left;
        //左归
        merge(left,mid);
        //右归
        merge(mid,right);
        //合并
        for (int k = left; k < right; k++)
            tmp[k] = nums[k];
        int limitL=mid;
        int i=left;
        while(left<limitL&&mid<right){
            if(tmp[left]>tmp[mid]){
                nums[i]=tmp[left++];
                count+=right-mid;
            }else{
                nums[i]=tmp[mid++];
            }
            i++;
        }
        while(left<limitL){
            nums[i++]=tmp[left++];
        }
        while(mid<right){
            nums[i++]=tmp[mid++];
        }
    }
}

另外我发现，我拷贝nums数组到tmp时，如果使用Arrays.copyOf()就会时间超限
使用System.arraycopy（）方法比直接for循环赋值也要慢。

剑指 Offer 55 - I. 二叉树的深度

剑指 Offer 55 - I. 二叉树的深度
遍历二叉树，每到一个结点，深度就取左右子树最长的那个。

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null)return 0;
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
}