第一门课：神经网络和深度学习 (Neural Networks and Deep Learning)

第三周：浅层神经网络(Shallow neural networks)

3.9 神 经 网 络 的 梯 度 下 降 （ Gradient descent for neural networks）

在这个视频中，我会给你实现反向传播或者说梯度下降算法的方程组，在下一个视频我们会介绍为什么这几个特定的方程是针对你的神经网络实现梯度下降的正确方程。

你的单隐层神经网络会有$W^{[1]},b^{[1]},W^{[2]},b^{[2]}$这些参数，还有个𝑛𝑥表示输入特征的个数，$n^{[1]}$表示隐藏单元个数，$n^{[2]}$表示输出单元个数。

矩阵$W^{[1]}$的维度就是$(n^{[1]},n^{[0]})$，$b^{[1]}$就是$n^{[1]}$维向量，可以写成$(n^{[1]},1)$，就是一个的列向量。 矩阵$W^{[2]}$的维度就是$(n^{[2]},n^{[1]})$，$b^{[2]}$的维就是$(n^{[2]},1)$维度。

你还有一个神经网络的成本函数，假设你在做二分类任务，那么你的成本函数等于：
Cost function: 公式： $J(W[1],b[1],W[2],b[2])=\frac{1}{m}{\sum }_{i=1}^{m}L(\hat{y},y)$
loss function 和之前做 logistic 回归完全一样。

训练参数需要做梯度下降，在训练神经网络的时候，随机初始化参数很重要，而不是初始化成全零。当你参数初始化成某些值后，每次梯度下降都会循环计算以下预测值：

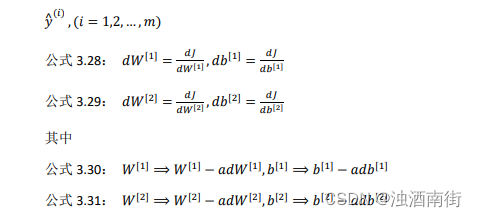
正向传播方程如下（之前讲过）：forward propagation：

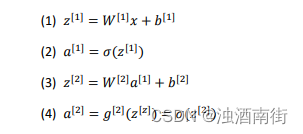
反向传播方程如下:back propagation：

上述是反向传播的步骤，注：这些都是针对所有样本进行过向量化，Y是1 ×m的矩阵；这里 np.sum 是 python 的 numpy 命令，axis=1 表示水平相加求和，keepdims 是防止python 输出那些古怪的秩数(n, )，加上这个确保阵矩阵$d{b}^{[2]}$这个向量输出的维度为(n, 1)这样标准的形式。

目前为止，我们计算的都和 Logistic 回归十分相似，但当你开始计算反向传播时，你需要计算，是隐藏层函数的导数，输出在使用 sigmoid 函数进行二元分类。这里是进行逐个元素乘积，因为$W^{[2]T}d{z}^{[2]}$和$(z[1])$这两个都为$(n^{[1]},m)$矩阵；

还有一种防止 python 输出奇怪的秩数，需要显式地调用 reshape 把 np.sum 输出结果写成矩阵形式。

以上就是正向传播的 4 个方程和反向传播的 6 个方程，这里我是直接给出的，在下个视频中，我会讲如何导出反向传播的这 6 个式子的。如果你要实现这些算法，你必须正确执行正向和反向传播运算，你必须能计算所有需要的导数，用梯度下降来学习神经网络的参数；你也可以许多成功的深度学习从业者一样直接实现这个算法，不去了解其中的知识。

3.10（选修）直观理解反向传播（Backpropagation intuition）

这个视频主要是推导反向传播。
下图是逻辑回归的推导：
回想一下逻辑回归的公式(参考公式 3.2、公式 3.5、公式 3.6、公式 3.15) 公式 3.38：

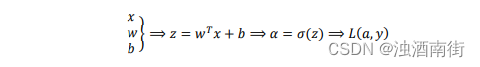
所以回想当时我们讨论逻辑回归的时候，我们有这个正向传播步骤，其中我们计算𝑧，然后𝑎，然后损失函数𝐿。

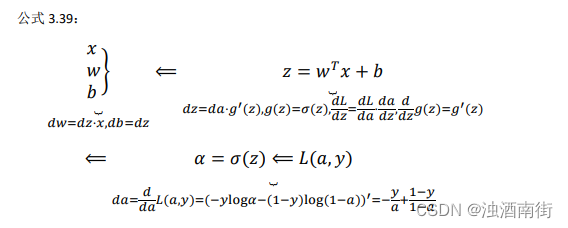
神经网络的计算中，与逻辑回归十分类似，但中间会有多层的计算。下图是一个双层神经网络，有一个输入层，一个隐藏层和一个输出层。

前向传播：
计算$z^{[1]}$，$a^{[1]}$，再计算$z^{[2]}$，$a^{[2]}$，最后得到 loss function。
反向传播：
向后推算出$d{a}^{[2]}$，然后推算出$d{z}^{[2]}$，接着推算出$d{a}^{[1]}$，然后推算出$d{z}^{[1]}$。我们不需要对x求导，因为x是固定的，我们也不是想优化x。向后推算出$d{a}^{[2]}$，然后推算出$d{z}^{[2]}$的步骤可以合为一步：

公式 3.40： $d{z}^{[2]}=a^{[2]}-y$， $d{W}^{[2]}=d{z}^{[2]}{a}^{[1]T}$(注意：逻辑回归中；为什么$a^{[1]T}$多了个转置：dw中的W(视频里是$W_i^{[2]}$)是一个列向量，而$W^{[2]}$是个行向量，故需要加个转置);

公式 3.41： $d{b}^{[2]}=d{z}^{[2]}$
公式3.42：KaTeX parse error: Double superscript at position 36: …^{[2]}∗ g^{[1]}'̲(z^{[1]}) 注意：这里的矩阵：W[2]的维度是：($n^{[2]}，n^{[1]}$)。
$z^{[2]}$ ， $d{z}^{[2]}$的维度都是：($n^{[2]},1$)，如果是二分类，那维度就是(1,1)。

$z^{[1]}$，$d{z}^{[1]}$的维度都是：($n^{[1]},1$)。
证明过程： 见公式 3.42，

其中$W^{[2]T}d{z}^{[2]}$维度为：($n^{[1]},n^{[2]}$)、($n^{[2]},1$)相乘得到($n^{[1]},1$)，和$z^{[1]}$维度相同，KaTeX parse error: Double superscript at position 8: g^{[1]}'̲(z^{[1]})的维度为($n^{[1]},1$)，这就变成了两个都是($n^{[1]},1$)向量逐元素乘积。
实现后向传播有个技巧，就是要保证矩阵的维度相互匹配。最后得到$d{W}^{[1]}和d{b}^{[1]}$，公式 3.43： $d{W}^{[1]}=d{z}^{[1]}{x}^T$, $d{b}^{[1]}=d{z}^{[1]}$可以看出$d{W}^{[1]}和d{W}^{[2]}$ 非常相似，其中x扮演了$a^{[0]}$的角色，$x^T$等同于$a^{[0]T}$。

下图写了主要的推导过程：

吴恩达老师认为反向传播的推导是机器学习领域最难的数学推导之一，矩阵的导数要用链式法则来求，如果这章内容掌握不了也没大的关系，只要有这种直觉就可以了。还有一点，就是初始化你的神经网络的权重，不要都是 0，而是随机初始化，下一章将详细介绍原因。