与二分搜索一样，跳转搜索是一种针对排序数组的搜索算法。基本思想是通过按固定步骤向前跳跃或跳过某些元素来代替搜索所有元素来检查更少的元素（比线性搜索）。例如，假设我们有一个大小为 n 的数组 arr[] 和一个大小为 m 的块（要跳转）。然后我们在索引 arr[0]、arr[m]、arr[2m]…..arr[km] 等中搜索。一旦找到区间 (arr[km] < x < arr[(k+1)m])，我们就从索引 km 执行线性搜索操作来查找元素 x。让我们考虑以下数组：(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610)。数组长度为 16。

假设要跳转的块大小为 4，跳转搜索将找到值 55，步骤如下：

步骤 1：从索引 0 跳转到索引 4；

步骤2：从索引4跳转到索引8；

步骤3：从索引8跳转到索引12；

步骤 4：由于索引 12 处的元素大于 55，因此我们将跳回到索引 8。

步骤 5：从索引 8 执行线性搜索以获取元素 55。

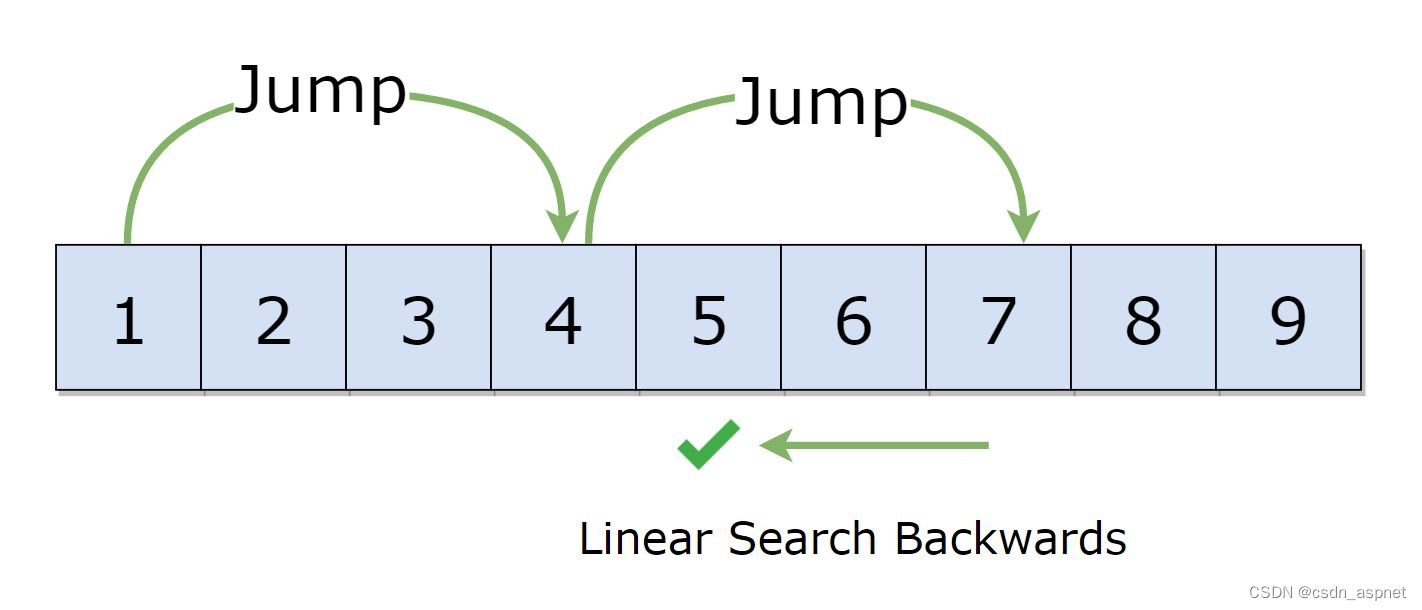
插图非示例

与线性搜索和二分搜索相比的性能：
        如果我们将它与线性搜索和二分搜索进行比较，那么它比线性搜索更好，但不比二分搜索更好。
性能递增顺序为：
        线性搜索 < 跳转搜索 < 二分搜索
要跳过的最佳块大小是多少？在最坏的情况下，我们必须进行 n/m 次跳转，如果最后检查的值大于要搜索的元素，我们会为线性搜索多执行 m-1 次比较。因此，最坏情况下的总比较次数将为((n/m) + m-1)。当 m = ?n 时，函数 ((n/m) + m-1) 的值最小。因此，最佳步长为 m = ?n。 

算法步骤
1、跳转搜索是一种通过跳过数组中的某些步骤来查找已排序数组中的特定值的算法。
2、步骤由数组长度的 sqrt 确定。 
以下是跳跃搜索的分步算法：
1、通过取数组 n 长度的 sqrt 来确定步长 m。
2、从数组的第一个元素开始，跳 m 步，直到该位置的值大于目标值。
        一旦找到大于目标的值，就从上一步开始进行线性搜索，直到找到目标或者明确目标不在数组中。
        如果找到目标，则返回其索引。如果没有，则返回 -1 表示在数组中未找到目标。 

示例：

// Java program to implement Jump Search.
public class JumpSearch
{
    public static int jumpSearch(int[] arr, int x)
    {
        int n = arr.length;
 
        // Finding block size to be jumped
        int step = (int)Math.floor(Math.sqrt(n));
 
        // Finding the block where element is
        // present (if it is present)
        int prev = 0;
        for (int minStep = Math.min(step, n)-1; arr[minStep] < x; minStep = Math.min(step, n)-1)
        {
            prev = step;
            step += (int)Math.floor(Math.sqrt(n));
            if (prev >= n)
                return -1;
        }
 
        // Doing a linear search for x in block
        // beginning with prev.
        while (arr[prev] < x)
        {
            prev++;
 
            // If we reached next block or end of
            // array, element is not present.
            if (prev == Math.min(step, n))
                return -1;
        }
 
        // If element is found
        if (arr[prev] == x)
            return prev;
 
        return -1;
    }
 
    // Driver program to test function
    public static void main(String [ ] args)
    {
        int arr[] = { 0, 1, 1, 2, 3, 5, 8, 13, 21,
                    34, 55, 89, 144, 233, 377, 610};
        int x = 55;
 
        // Find the index of 'x' using Jump Search
        int index = jumpSearch(arr, x);
 
        // Print the index where 'x' is located
        System.out.println("\nNumber " + x +
                            " is at index " + index);
    }
} 

输出：
        数字 55 位于索引 10
时间复杂度：O(?n) 
辅助空间：O(1)

跳转搜索的优点：
        1、比元素均匀分布的数组的线性搜索更好。
        2、与大型数组的线性搜索相比，跳跃搜索的时间复杂度较低。
        3、跳跃搜索的步数与数组大小的平方根成正比，对于大型数组来说效率更高。
        4、与二分搜索或三元搜索等其他搜索算法相比，它更容易实现。
        5、跳转搜索适用于元素有序且均匀分布的数组，因为它可以在每次迭代时跳转到数组中更接近的位置。

要点：
        1、仅适用于排序数组。
        2、所要跳转的块的最佳大小是(?n)。这使得跳转搜索的时间复杂度为O(?n)。
        3、跳转搜索的时间复杂度介于线性搜索 ((O(n)) 和二分搜索 (O(Log n)) 之间。
        4、二分查找比跳转查找要好，但是跳转查找的优点是我们只需要回溯一次（二分查找可能需要最多 O(Log n) 次跳转，考虑要查找的元素是最小元素或者更大的元素的情况比最小的）。因此，在二分搜索成本高昂的系统中，我们使用跳转搜索。