312. 乌龟棋 - AcWing题库

所需知识：动态规划

闫氏dp分析法：

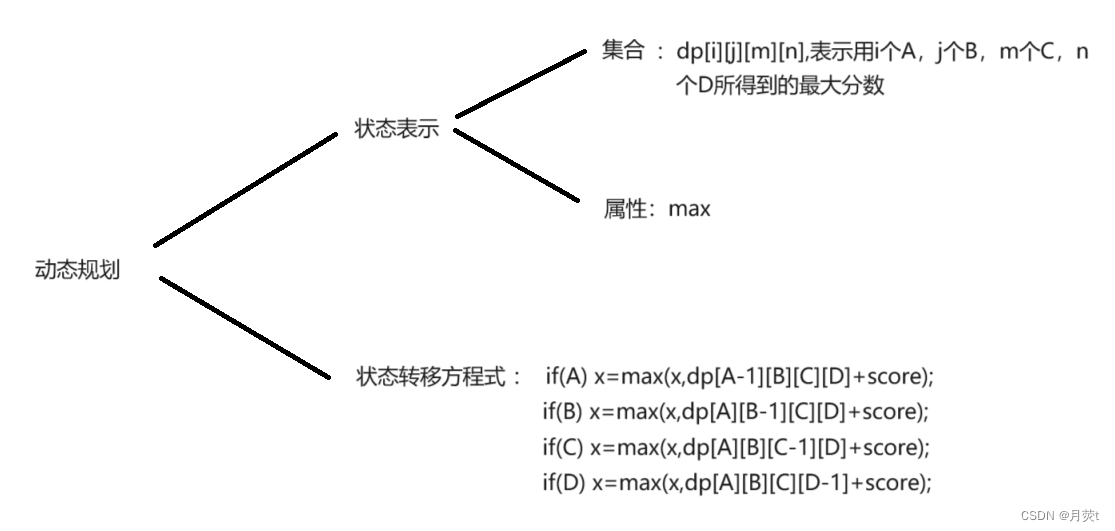
整体思路：由于走的方式有四种，所以dp[i][j][m][n]的来源有四种，状态转移方程式要求不重不漏，所以我们可以以使用的最后一个卡片上的数值来进行分类。

代码书写：首先我们将每种卡片的数量记录下来，状态转移时，必须要有此卡片才能进行转移，例：如果前面已经将A卡片用完了，后面就不能再使用A了；然后将dp[0][0][0][0]初始化为a[1]，因为最初停在第一个位置，之后将所有状态遍历一遍，找出最大值，输出答案；

C++代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

int a[355],b[165];
int dp[41][41][41][41];
int N,M;
int main()
{
    cin>>N>>M;
    for (int i = 1; i <= N; i ++ ){
        cin>>a[i];
    }
    for (int i = 1; i <= M; i ++ ){
        int x;
        cin>>x;
        b[x]++;
    }
    dp[0][0][0][0]=a[1];
    for(int A=0;A<=b[1];A++){
        for(int B=0;B<=b[2];B++){
            for(int C=0;C<=b[3];C++){
                for(int D=0;D<=b[4];D++){
                    int score=a[A+2*B+3*C+4*D+1];
                    int &x=dp[A][B][C][D];
                    if(A) x=max(x,dp[A-1][B][C][D]+score);
                    if(B) x=max(x,dp[A][B-1][C][D]+score);
                    if(C) x=max(x,dp[A][B][C-1][D]+score);
                    if(D) x=max(x,dp[A][B][C][D-1]+score);
                }
            }
        }
    }
    cout<<dp[b[1]][b[2]][b[3]][b[4]];
    return 0;
}