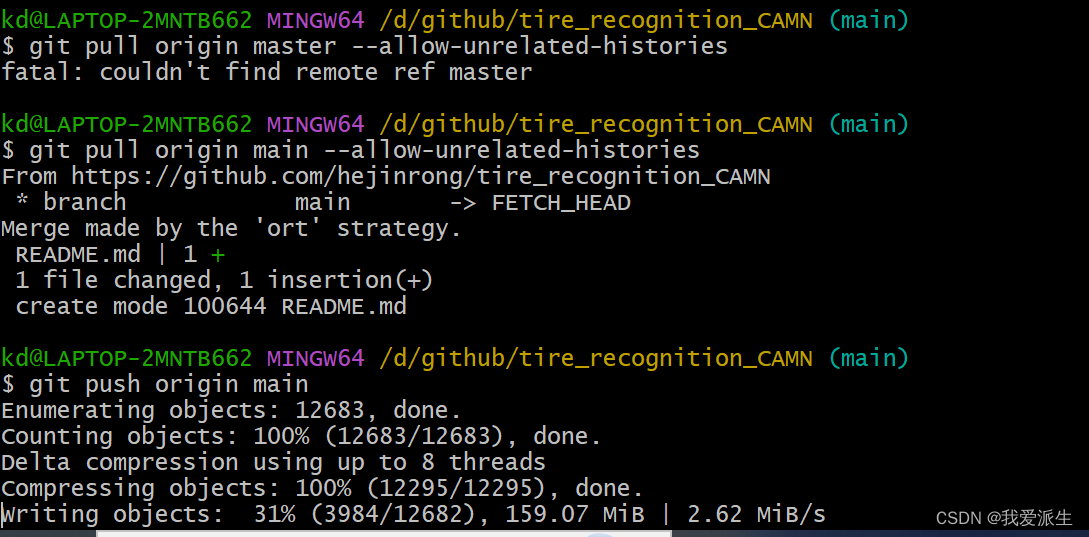
例题——最大序列和

找状态

思路一（×）

定义一个状态$dp[i]$，计为前i个数构成子序列和的最大值
此法状态转移比较困难，即若$dp[i]$与$dp[i-1]$没有明确的关系，有可能两个子序列和取在不同的连续子串上

思路二（√）

同样定义一个状态$dp[i]$，计为前i个数构成子序列和的最大值，但与思路一不同的是，这次的$dp[i]$中必须包含序列中最后一个结点（即前i个结点中第i个结点），从而能够构建$dp[i]$与$dp[i-1]$的关系
破题绝招：假设已知$dp[i]$（包含最后一个结点），那么：

• 当$dp[i]$就是最大子序和时，有a[i]>0且a[i+1]<0
• 当$dp[i]>=0$时，必有：$dp[i+1]=a[i+1]+dp[i]$
• 当$dp[i]<0$时，必有：$dp[i+1]=a[i+1]$

当我们求出所有的$dp[i]$，求最大值即可

代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <climits>
//#include <bits/stdc++.h>
using namespace std;
long long a[1000001];
long long dp[1000001];
long long max_subsequence(int n){
    long long maximum = LONG_LONG_MIN;
    for (int i = 0; i < n; ++i) {
        if (i==0){
            dp[i] = a[i];
        } else{
            dp[i] = max(a[i],a[i]+dp[i-1]);
        }
        maximum = max(maximum,dp[i]);
    }
    return maximum;
}


int main() {
    int n;
    while(scanf("%d",&n)!=EOF){
        for (int i = 0; i < n; ++i) {
            scanf("%lld",&a[i]);
        }
        printf("%lld\n", max_subsequence(n));
    }
    return 0;
}