Bezier曲线

1. 实验要求

2. Bezier曲线的原理以及公式推导

参考贝塞尔曲线（Bezier Curve）原理及公式推导_bezier曲线-CSDN博客

Bezier曲线的一些特性：

使用n个控制点 $\left \{ P_{1},P_{2},P_{3}......P_{n} \right \}$ 来控制曲线形状

曲线通过起始点 $P_{1}$ 和终止点 $P_{n}$ ，接近但不通过中间点 $P_{2}-P_{n-1}$

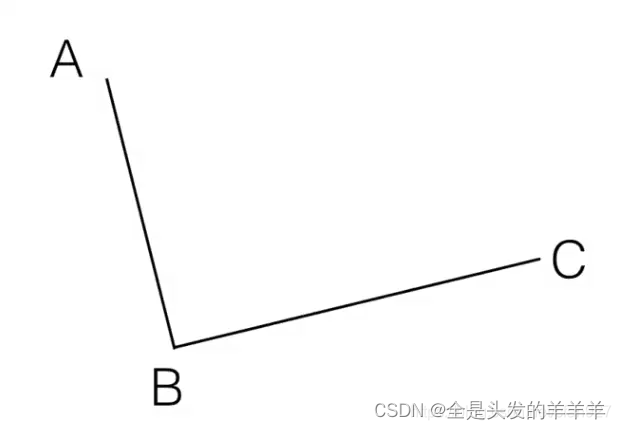
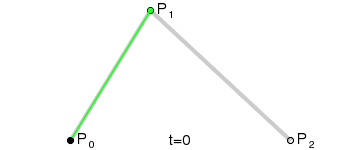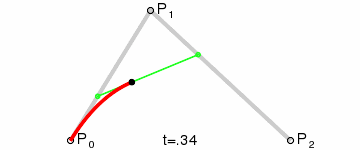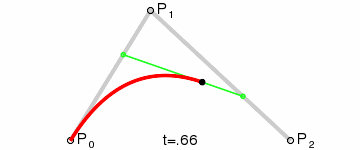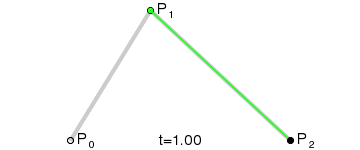
2.1 直观理解

Step 1. 在二维平面内选三个不同的点并依次用线段连接

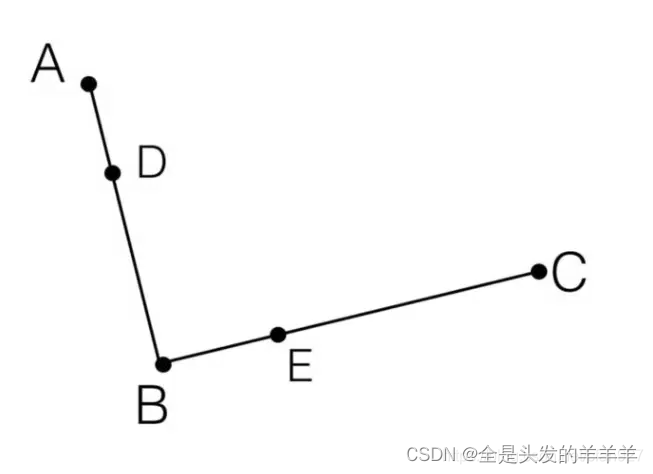
Step 2. 在线段AB 和BC 上找到 D、E 两点，使得 $\frac{AD}{DB}=\frac{BE}{EC}$

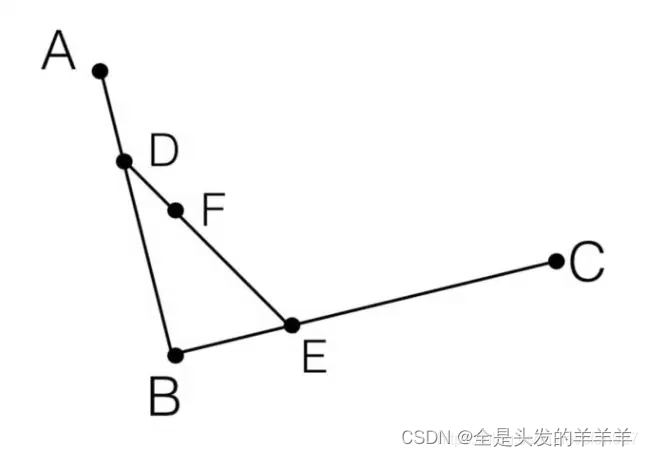
Step 3. 连接DE ，并在 DE 上找到 F 点，使其满足 $\frac{DF}{FE}=\frac{AD}{DB}=\frac{BE}{EC}$ 抛物线的三切定理

Step 4. 找出符合上述条件的所有点

2.2 bezier曲线公式

一次贝塞尔曲线： $B(t) = (1-t)P_{0} + tP_{1} ,t\epsilon [0,1]$

二次贝塞尔曲线： $B(t) = (1-t)^{2} P_{0} + 2t(1-t) P_{1} + t^{2} P_{2}, t\epsilon [0,1]$

三次贝塞尔曲线： $B(t) = (1-t)^{3} P_{0} + 3t(1-t)^{2} P_{1} + 3t^{2}(1-t) P_{2}+t^{3}P_{3}, t\epsilon [0,1]$

3. 简单的三次贝塞尔曲线的绘制

使用PyOpenGL（环境的配置可以查看PyOpenGL环境配置教程-CSDN博客

from OpenGL.GL import *
from OpenGL.GLUT import *
import numpy as np

# 控制点
control_points = [(-0.5, -0.5), (-0.6, 0.25), (0.25, 0.25), (0.75, -0.5)]


# 计算Bezier曲线上的点
def bezier_curve(control_points, t):
    n = len(control_points) - 1
    result = [0, 0]
    for i in range(n + 1):
        result[0] += control_points[i][0] * binomial_coefficient(n, i) * ((1 - t) ** (n - i)) * (t ** i)
        result[1] += control_points[i][1] * binomial_coefficient(n, i) * ((1 - t) ** (n - i)) * (t ** i)
    return result


# 计算二项式系数
def binomial_coefficient(n, k):
    result = 1
    for i in range(1, k + 1):
        result *= (n - i + 1) / i
    return result


# 绘制Bezier曲线
def draw_bezier_curve():
    glBegin(GL_LINE_STRIP)
    for t in np.arange(0, 1.01, 0.01):
        point = bezier_curve(control_points, t)
        glVertex2fv(point)
    glEnd()

    # 绘制控制点
    glColor3f(1.0, 0.0, 0.0)  # 设置控制点颜色为红色
    glPointSize(5.0)  # 设置控制点大小
    glBegin(GL_POINTS)
    for point in control_points:
        glVertex2fv(point)
    glEnd()

    # 将相邻的控制点连线
    glColor3f(0.0, 1.0, 0.0)  # 设置连线颜色为绿色
    glBegin(GL_LINES)
    for i in range(len(control_points) - 1):
        glVertex2fv(control_points[i])
        glVertex2fv(control_points[i + 1])
    glEnd()


def display():
    glClear(GL_COLOR_BUFFER_BIT)
    glColor3f(1.0, 1.0, 1.0)
    draw_bezier_curve()
    glFlush()


def main():
    glutInit()
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB)
    glutInitWindowSize(400, 400)
    glutCreateWindow(b"Bezier Curve")

    glClearColor(0.0, 0.0, 0.0, 0.0)
    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()
    glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0)
    glMatrixMode(GL_MODELVIEW)

    glutDisplayFunc(display)

    glutMainLoop()


if __name__ == "__main__":
    main()

结果

修改控制点

control_points = [(-0.5, -0.5), (0, 0.5), (0.25, -0.25), (0.5, 0.25), (0.75, 0),(0.6,-0.1)]

得到5阶贝塞尔曲线

4.增加交互功能

4.1 实现鼠标可以拖动控制点

添加了两个函数，鼠标的控制

from OpenGL.GL import *
from OpenGL.GLUT import *
import numpy as np

# 控制点
control_points = [(-0.5, -0.5), (0, 0.5), (0.25, -0.25), (0.5, 0.25), (0.75, 0),(0.6,-0.1)]

# 选中的控制点索引
selected_point_index = -1

# 计算Bezier曲线上的点
def bezier_curve(control_points, t):
    n = len(control_points) - 1
    result = [0, 0]
    for i in range(n + 1):
        result[0] += control_points[i][0] * binomial_coefficient(n, i) * ((1 - t) ** (n - i)) * (t ** i)
        result[1] += control_points[i][1] * binomial_coefficient(n, i) * ((1 - t) ** (n - i)) * (t ** i)
    return result

# 计算二项式系数
def binomial_coefficient(n, k):
    result = 1
    for i in range(1, k + 1):
        result *= (n - i + 1) / i
    return result

# 鼠标点击事件处理函数
def mouse(button, state, x, y):
    global selected_point_index
    if button == GLUT_LEFT_BUTTON and state == GLUT_DOWN:
        # 将鼠标点击位置的窗口坐标转换为归一化坐标
        x_normalized = 2 * (x / glutGet(GLUT_WINDOW_WIDTH)) - 1
        y_normalized = 1 - 2 * (y / glutGet(GLUT_WINDOW_HEIGHT))

        # 寻找离鼠标点击位置最近的控制点
        min_distance = float('inf')
        for i, point in enumerate(control_points):
            distance = np.sqrt((x_normalized - point[0]) ** 2 + (y_normalized - point[1]) ** 2)
            if distance < min_distance:
                min_distance = distance
                selected_point_index = i



# 鼠标移动事件处理函数
def motion(x, y):
    global selected_point_index
    if selected_point_index != -1:
        # 将鼠标位置的窗口坐标转换为归一化坐标
        x_normalized = 2 * (x / glutGet(GLUT_WINDOW_WIDTH)) - 1
        y_normalized = 1 - 2 * (y / glutGet(GLUT_WINDOW_HEIGHT))

        # 更新选中控制点的坐标
        control_points[selected_point_index] = (x_normalized, y_normalized)

    glutPostRedisplay()  # 通知OpenGL窗口需要重新绘制


# 绘制函数
def draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glColor3f(1.0, 1.0, 1.0)

    # 绘制Bezier曲线
    glBegin(GL_LINE_STRIP)
    for t in np.arange(0, 1.01, 0.01):
        point = bezier_curve(control_points, t)
        glVertex2fv(point)
    glEnd()

    # 绘制控制点
    glColor3f(1.0, 0.0, 0.0)
    glPointSize(5.0)
    glBegin(GL_POINTS)
    for point in control_points:
        glVertex2fv(point)
    glEnd()

    # 连接相邻的控制点
    glColor3f(0.0, 1.0, 0.0)
    glBegin(GL_LINES)
    for i in range(len(control_points) - 1):
        glVertex2fv(control_points[i])
        glVertex2fv(control_points[i + 1])
    glEnd()

    glFlush()

# 主函数
def main():
    glutInit()
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB)
    glutInitWindowSize(400, 400)
    glutCreateWindow(b"Bezier Curve")

    glClearColor(0.0, 0.0, 0.0, 0.0)
    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()
    glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0)
    glMatrixMode(GL_MODELVIEW)

    glutMouseFunc(mouse)
    glutMotionFunc(motion)
    glutDisplayFunc(draw)

    glutMainLoop()

if __name__ == "__main__":
    main()

结果5阶bezier鼠标拖动演示-CSDN直播

5阶bezier鼠标拖动演示

4.2 采用鼠标添加控制点

from OpenGL.GL import *
from OpenGL.GLUT import *
import numpy as np

# 控制点
control_points = []

# 是否允许添加新的控制点
allow_adding_points = True

# 是否处于控制点移动模式
is_move_mode = False

# 选中的控制点索引
selected_point_index = -1


# 计算Bezier曲线上的点
def bezier_curve(control_points, t):
    n = len(control_points) - 1
    result = [0, 0]
    for i in range(n + 1):
        result[0] += control_points[i][0] * binomial_coefficient(n, i) * ((1 - t) ** (n - i)) * (t ** i)
        result[1] += control_points[i][1] * binomial_coefficient(n, i) * ((1 - t) ** (n - i)) * (t ** i)
    return result


# 计算二项式系数
def binomial_coefficient(n, k):
    result = 1
    for i in range(1, k + 1):
        result *= (n - i + 1) / i
    return result


# 鼠标点击事件处理函数
# 鼠标点击事件处理函数
def mouse(button, state, x, y):
    global allow_adding_points, selected_point_index, is_move_mode
    if allow_adding_points and button == GLUT_LEFT_BUTTON and state == GLUT_DOWN:
        # 将鼠标点击位置的窗口坐标转换为归一化坐标
        x_normalized = 2 * (x / glutGet(GLUT_WINDOW_WIDTH)) - 1
        y_normalized = 1 - 2 * (y / glutGet(GLUT_WINDOW_HEIGHT))

        # 添加新的控制点
        control_points.append((x_normalized, y_normalized))

        # 通知OpenGL窗口需要重新绘制
        glutPostRedisplay()
    elif button == GLUT_LEFT_BUTTON and state == GLUT_DOWN:
        # 寻找离鼠标点击位置最近的控制点
        min_distance = float('inf')
        for i, point in enumerate(control_points):
            distance = np.sqrt((2 * x / glutGet(GLUT_WINDOW_WIDTH) - 1 - point[0]) ** 2 + (
                        1 - 2 * y / glutGet(GLUT_WINDOW_HEIGHT) - point[1]) ** 2)
            if distance < min_distance:
                min_distance = distance
                selected_point_index = i
        if min_distance < 0.05:  # 如果鼠标点击到了控制点附近，则进入控制点移动模式
            is_move_mode = True
    elif button == GLUT_LEFT_BUTTON and state == GLUT_UP:
        is_move_mode = False
        selected_point_index = -1


# 鼠标移动事件处理函数
def motion(x, y):
    global selected_point_index, is_move_mode
    if is_move_mode:
        # 将鼠标位置的窗口坐标转换为归一化坐标
        x_normalized = 2 * (x / glutGet(GLUT_WINDOW_WIDTH)) - 1
        y_normalized = 1 - 2 * (y / glutGet(GLUT_WINDOW_HEIGHT))

        # 更新选中控制点的坐标
        control_points[selected_point_index] = (x_normalized, y_normalized)

        # 通知OpenGL窗口需要重新绘制
        glutPostRedisplay()


# 键盘事件处理函数
def keyboard(key, x, y):
    global allow_adding_points
    if key == b'\r':  # 按下回车键
        allow_adding_points = False
    elif key == b'\x1b':  # 按下ESC键
        allow_adding_points = True


# 绘制函数
def draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glColor3f(1.0, 1.0, 1.0)

    # 绘制Bezier曲线
    glBegin(GL_LINE_STRIP)
    for t in np.arange(0, 1.01, 0.01):
        point = bezier_curve(control_points, t)
        glVertex2fv(point)
    glEnd()

    # 绘制控制点
    glColor3f(1.0, 0.0, 0.0)
    glPointSize(5.0)
    glBegin(GL_POINTS)
    for point in control_points:
        glVertex2fv(point)
    glEnd()

    # 连接相邻的控制点
    glColor3f(0.0, 1.0, 0.0)
    glBegin(GL_LINES)
    for i in range(len(control_points) - 1):
        glVertex2fv(control_points[i])
        glVertex2fv(control_points[i + 1])
    glEnd()

    glFlush()


# 主函数
def main():
    glutInit()
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB)
    glutInitWindowSize(400, 400)
    glutCreateWindow(b"Bezier Curve")

    glClearColor(0.0, 0.0, 0.0, 0.0)  # 将窗体的背景色设置为黑色

    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()
    glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0)
    glMatrixMode(GL_MODELVIEW)

    glutMouseFunc(mouse)
    glutMotionFunc(motion)
    glutDisplayFunc(draw)
    glutKeyboardFunc(keyboard)

    glutMainLoop()


if __name__ == "__main__":
    main()

结果

bezier曲线（鼠标添加控制点+鼠标拖动控制点