一、优先级队列的定义和存储
优先级队列定义:优先级高的元素在队头,优先级低的元素在队尾
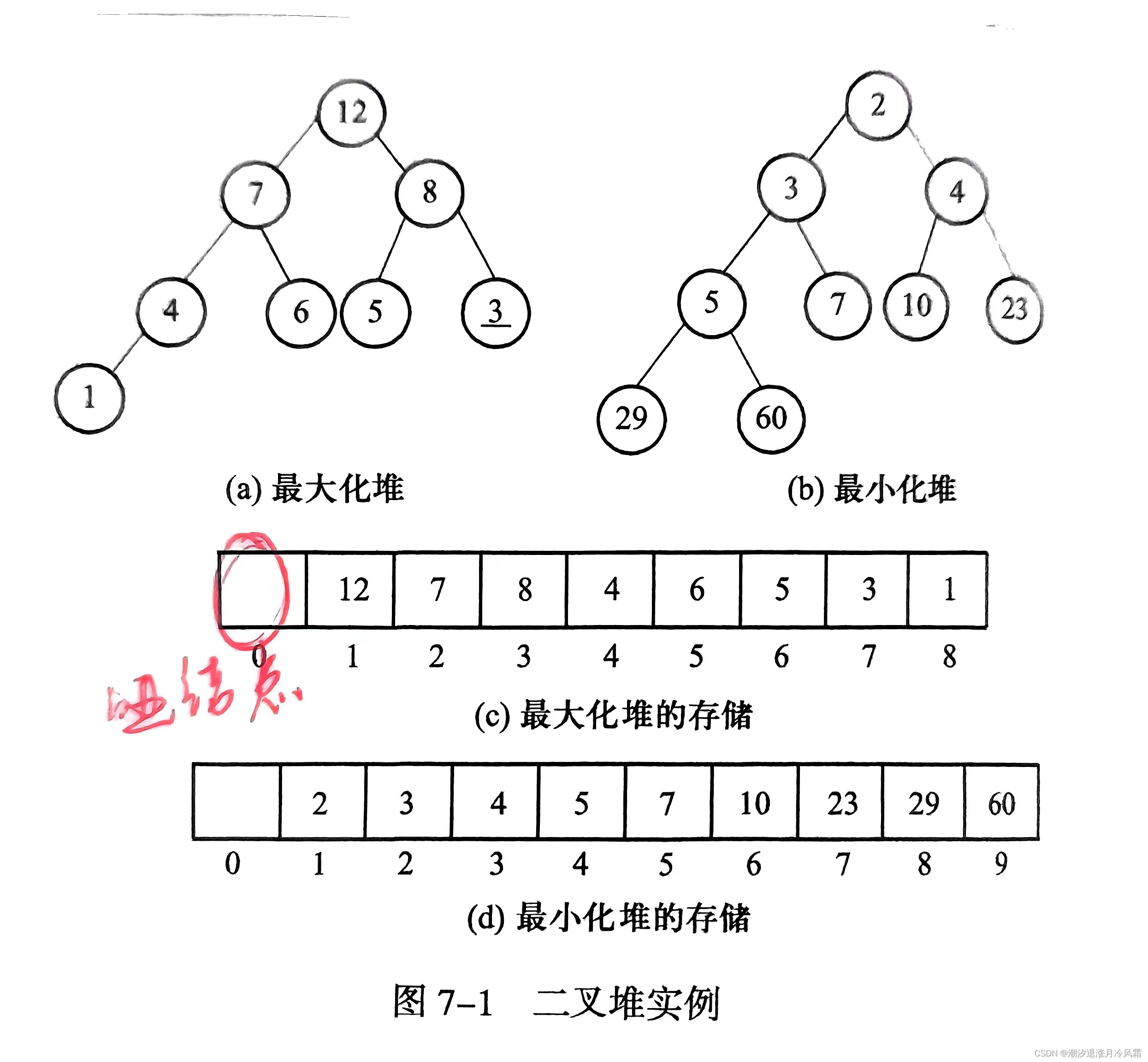
基于普通线性表实现优先级队列,入队和出队中必有一个时间复杂度O(n),基于二叉树结构实现优先级队列,能够让入队和出队时间复杂度都为O(logn),这种基于树状结构的优先级队列也称为二叉堆。当根结点为最大元素时,称为最大化堆或大顶堆;当根结点为最小元素时,称为最小化堆或小顶堆。二叉堆是有序的完全二叉树,使用顺序存储,留出数组第一个位置作为哑结点,如图所示:
二、优先级队列的运算实现
先学习优先级队列的两大核心运算:入队和出队,之后再介绍如何建堆。下面以小顶堆为例分析。
2.1 入队:上滤插入
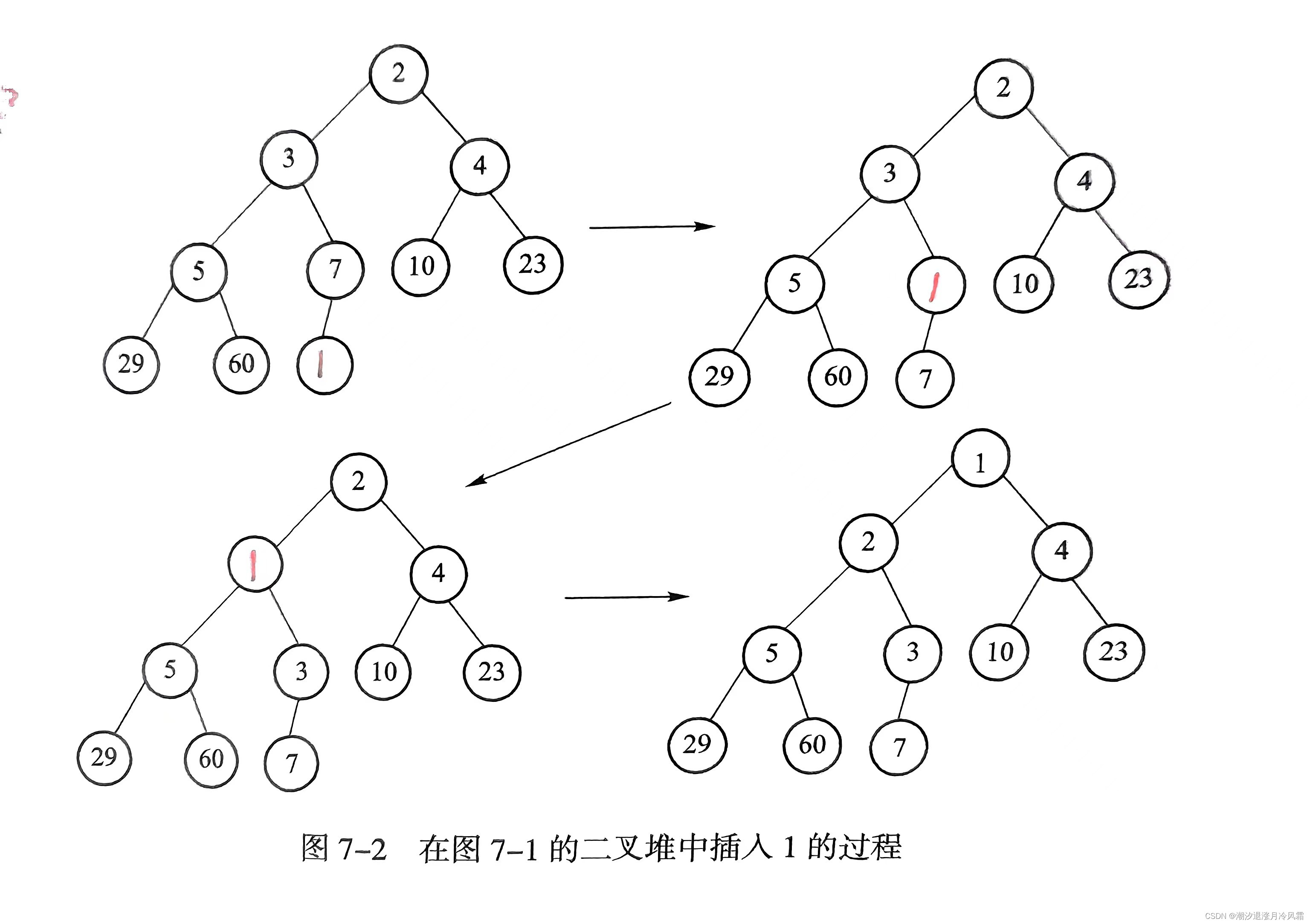
在原有的二叉堆上插入新元素,同时使其维持有序性,可以通过“上滤”实现。第一步是寻找新元素应插入的位置,第二步是插入新元素,时间复杂度为O(logn)
//先将新元素放在二叉堆最底部 int hole=++currentlength; //与父结点比较,决定是否交换(实际上不需要交换,因为新元素不一定到达最终插入位置),条件:比父结点值小,上滤过程持续进行,设置循环; //循环结束条件:到达堆顶(hole=1)或已到达最终插入位置 while(hole>1&&x<array[hole/2]) { array[hole]=array[hole/2]; //父结点下移 hole/=2; //更新新元素位置 } //插入元素 array[hole]=x;
2.2 出队:下滤删除
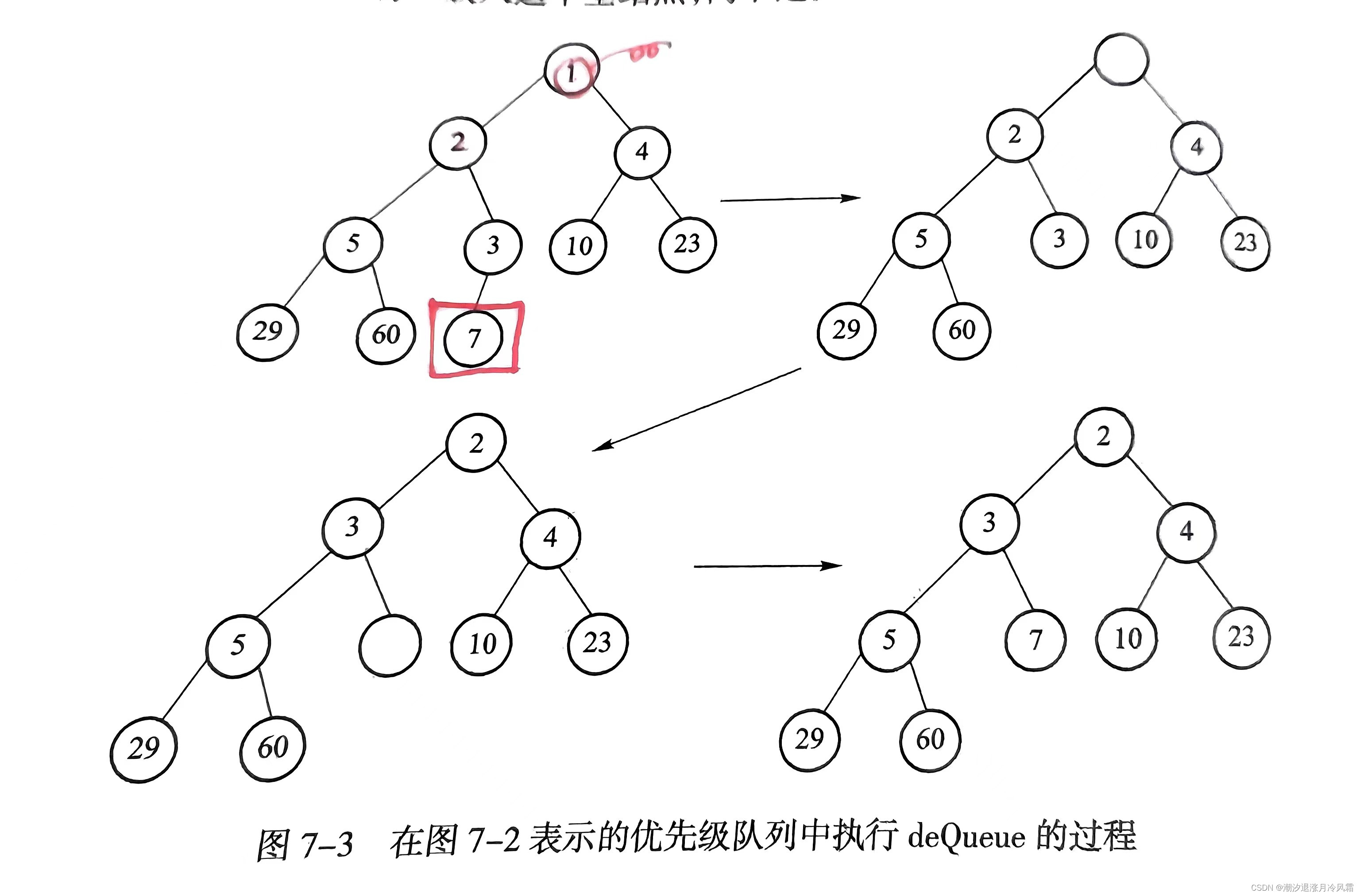
现在要删除队头元素,也就是堆顶元素,简单的想法是和孩子节点比较,选择其中较小的上滤,可这样可能会破坏二叉堆完全二叉树的结构[比如1 3 2 4 5删除后2 3 null 45],为了维持完全二叉树的结构,我们需要考虑为堆最后一个结点重新寻找位置。如图所示,将最后一个节点放在堆顶再下滤,就能实现删除堆顶元素并使二叉树结点数量减一。[比如1 3 2 4 5->
5 3 2 4->2 3 5 4],时间复杂度为O(logn)
//把最后一个元素放在堆顶 tmp=array[1]=array[currentlength--]; hole=1; //叶子结点条件 2i>n,非叶子结点条件:2i<=n while(2*hole<=currentlength){ //选择较小子节点 child=2*hole; if(2*hole!=currentlength) if(array[child]>array[child+1]) child++; //下滤 if(tmp>array[child]) { array[hole]=array[child]; hole=child; } //否则下滤结束 else break; //否则选择左孩子结点上滤 }
2.3 建堆
在构造函数中传入数据数组初始化二叉堆,最简单的想法是对N个元素执行N次入队操作,每次入队后对维持二叉堆有序性,时间复杂度O(nlogn);如何提升时间效率呢,可以先用原始数据初始化二叉堆,再从最后一个非叶节点开始到第一个结点,依次执行下滤操作,这样调用percolateDown(i)时保证结点i的所有自堆都满足有序性,这样自下往上,从局部有序最后抵达全局有序,可以证明这种建堆方式时间复杂度为O(n)。
对2.2中的代码略微修改容易得到下滤函数:
//下滤函数 precolateDown实现 tmp=array[i]; hole=i; while(2*hole<=currentlength){ child=2*hole; if(2*hole!=currentlength) if(array[child]>array[child+1]) child++; if(tmp>array[child]) { array[hole]=array[child]; hole=child; } else break;建堆过程可以表示为
//建堆 buildHeap 实现 for(int i=currentlength/2;i>0;i--){ precolateDown(i); }
三、 STL中的优先级队列
类模板名:priority_queue
头文件:queue
定义:priority<elemtype,base container(默认 vector),(默认大顶堆,添加谓词greater<int>则定义小顶堆)>
成员函数:
void push() 入队
void pop() 出队
Elemtype top() 获取队头元素
void clear() 清空
bool empty() 判空
四、D堆
D堆就是D叉树,由于生成的堆更矮,入队的时间复杂度为
,比二叉堆更加优越。
但出队时就不一样了,由于需要比较子结点,若采用最简单的选择算法,则时间复杂度为
,因此D堆适用于插入操作比删除操作多非常多的场景。
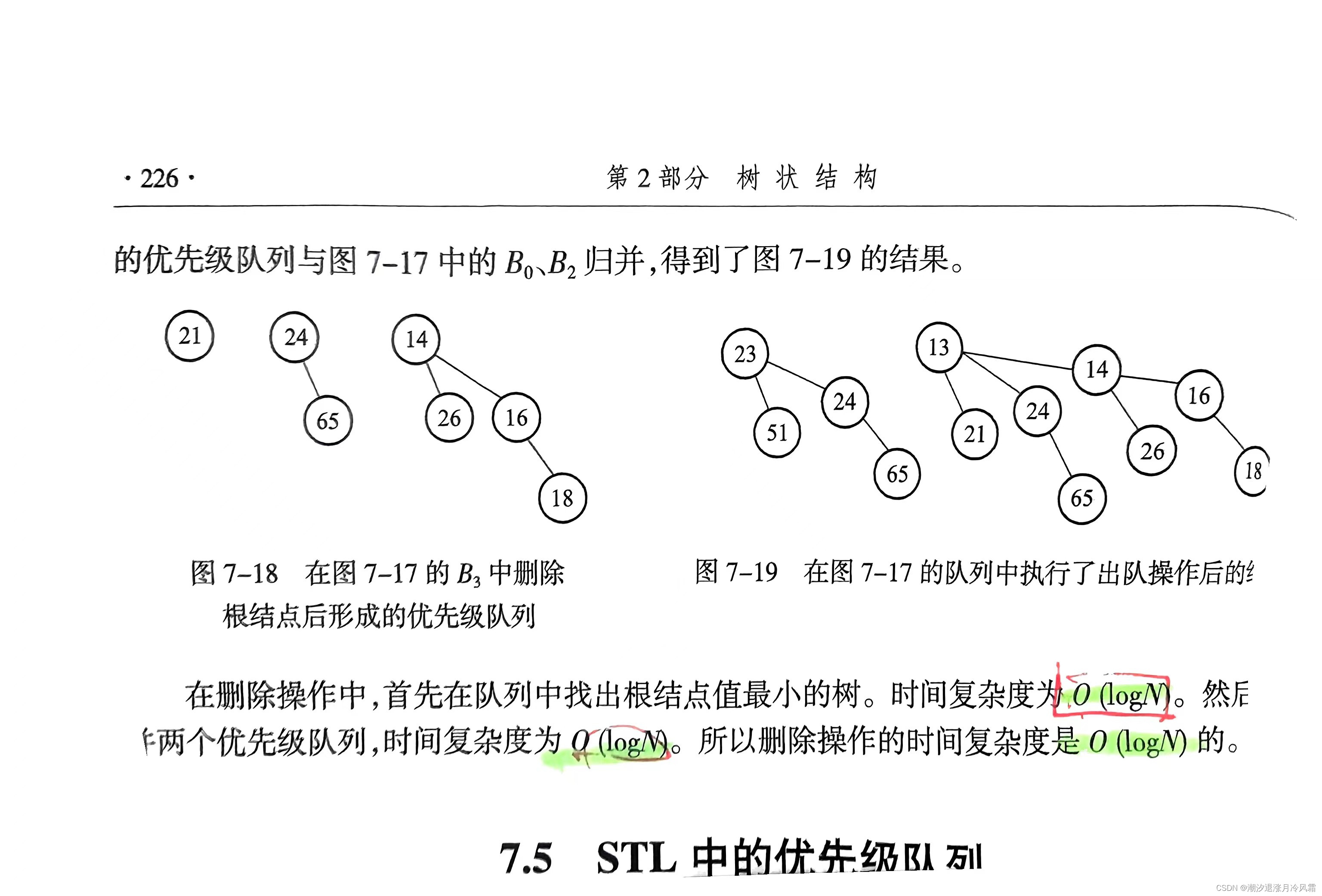
五、归并优先级队列(了解)
归并:即合并两棵有序树,在前面我们做过合并二叉树的题目,归并可通过递归实现
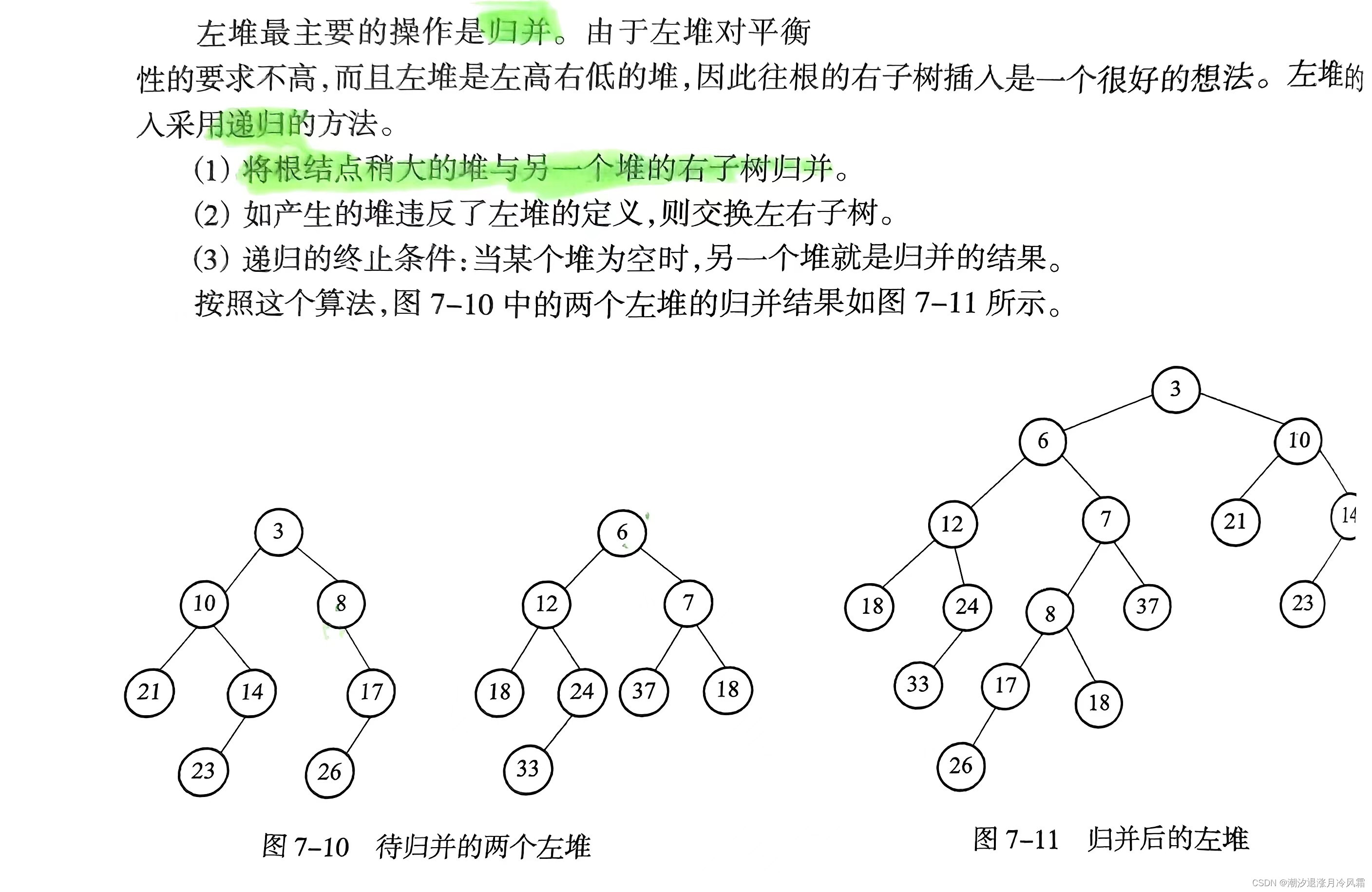
5.1 左堆
这里的nql容易通过递归实现,参考二叉树中刷题中的类似题目。

5.2 斜堆

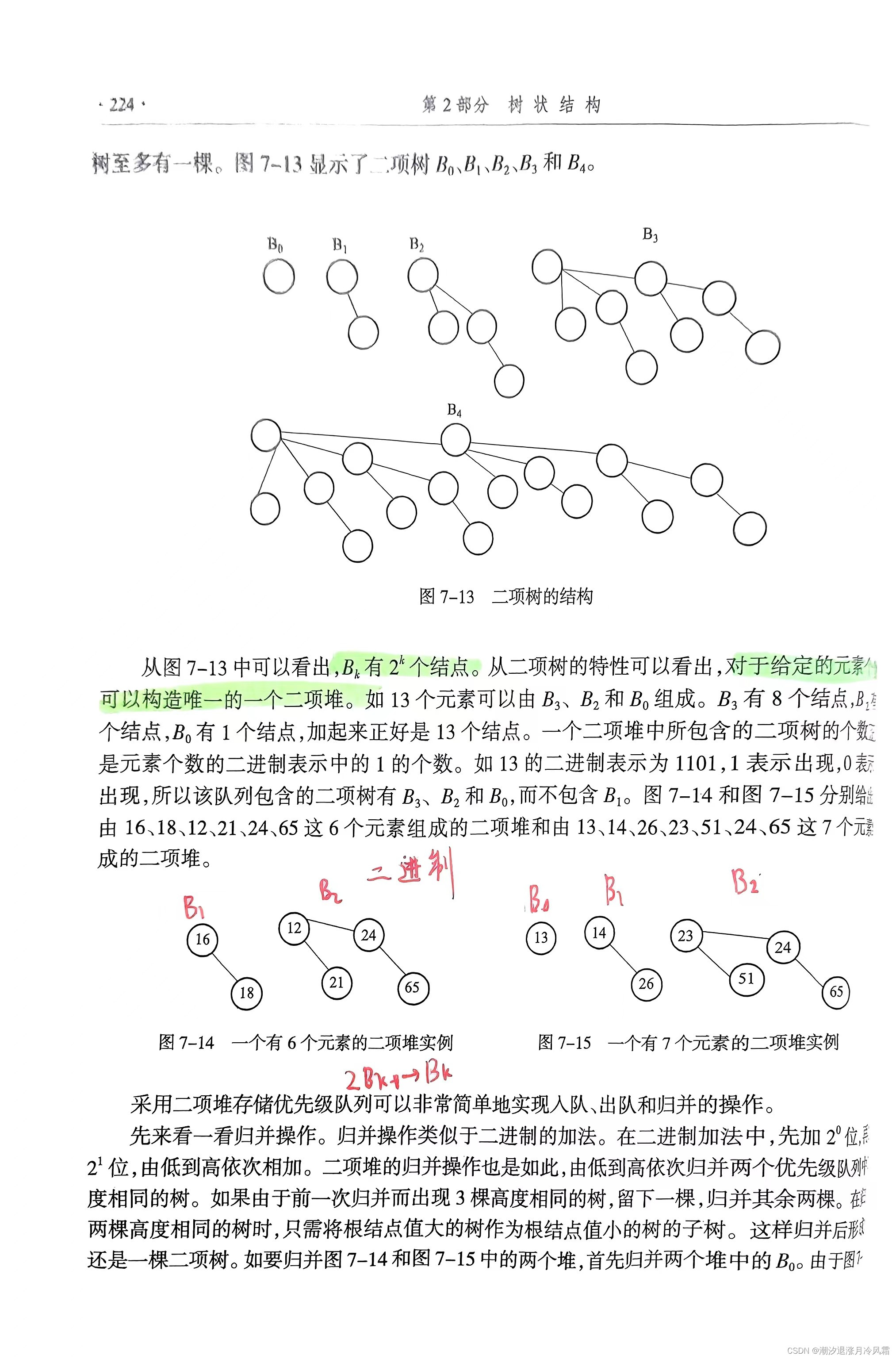
5.3 二项堆
二项堆和二进制有很大相似性,归并的过程也像二进制加法


六、多服务台排队系统模拟
#include<queue>
#include<ctime>
#include<cstdlib>
#include<iostream>
using namespace std;
class simulator { //模拟类
private:
enum IO { IN, OUT };
struct event {//事件类型
IO io; //事件性质:顾客到达/顾客离开
int serviceNo; //服务柜台编号
int eventTime; //事件时间
int customNo; //顾客编号
};
struct compare {
bool operator()(const event& e1, const event& e2)
{
return e1.eventTime > e2.eventTime;
}
};
int* service; //服务台
priority_queue<event, deque<event>, compare> Main; //处理事件队列,按照事件时间优先级排列,事件时间越早,优先级越高
queue<event> Wait; //排队队列
int customNum; //顾客数量
int serviceNum; //服务台数量
int serviceTimeMax; //最长服务时间
int serviceTimeMin; //最短服务时间
int arriveLow;//允许到达最早时间
int arriveHigh; //允许到达最晚时间
int searchFree(); //寻找空闲服务台,找不到返回-1
int currentTime; //模拟中当前时间
public:
simulator(int sTMax, int sTMin, int cusNum, int serNum,int arL,int arH) {
customNum = cusNum;
serviceNum = serNum;
serviceTimeMax = sTMax;
serviceTimeMin = sTMin;
arriveLow = arL;
arriveHigh = arH;
service = new int[serNum] {0};//将所有服务台置于空闲状态(0)
currentTime = 0;
};
void Simulation(); //模拟整个排队过程
};
int simulator::searchFree()
{
for (int i = 0; i < serviceNum; i++)
{
if (service[i]==0) return i;
}
return -1;
}
void simulator::Simulation()
{
//产生顾客的服务时间,并存入队列
event* Eve;
Eve=new event[customNum];
for (int i = 0; i < customNum; i++)
{
Eve[i].io = IN;
Eve[i].eventTime = arriveLow + rand() % (arriveHigh - arriveLow + 1);
Eve[i].serviceNo = -1; //未服务
Eve[i].customNo = i;
Main.push(Eve[i]);
}
//开始处理事件
while (!Main.empty())
{
int index;
event tmp = Main.top();
Main.pop();
currentTime = tmp.eventTime; //更新当前时间
switch (tmp.io) {
case IN: //处理到达事件
if ((index=searchFree())!=-1) //存在空闲服务台,让顾客前往该服务台
{
service[index] = 1;
tmp.serviceNo = index;
//将时间修改为离开事件,并随机生成其业务服务时间,修改事件时间,重新入队
tmp.io = OUT;
int Stime = serviceTimeMin + rand() % (serviceTimeMax - serviceTimeMin + 1);
tmp.eventTime += Stime;
Main.push(tmp);
cout << "当前时间:" << currentTime << endl;
cout << "服务台" << index << "正在服务顾客" << tmp.customNo << ",服务时长预计" << Stime << "分钟" << endl;
}
else { //不存在空闲服务台,让顾客排队等待
Wait.push(tmp);
}
break;
case OUT:
int NO = tmp.serviceNo;
cout << "当前时间:" << currentTime << endl;
cout << "服务台" << NO << "完成服务顾客" << tmp.customNo << endl;
//排队队列非空,让排队队列第一个人接受空出服务台服务
if (!Wait.empty())
{
event tmp2 = Wait.front();
Wait.pop();
int Stime = serviceTimeMin + rand() % (serviceTimeMax - serviceTimeMin + 1);
tmp2.eventTime = currentTime+Stime;
tmp2.io = OUT;
tmp2.serviceNo = NO;
Main.push(tmp2);
cout << "当前时间:" << currentTime << endl;
cout << "服务台" << NO << "正在服务顾客" << tmp2.customNo << ",服务时长预计" << Stime << "分钟" << endl;
}
else {
service[NO] = 0;
}
break;
}
}
}
int main()
{
srand(time(NULL));
int sTMax, sTMin, cusNum, serNum, arL, arH;
cout << "输入柜台数:" << endl;
cin >> serNum;
cout << "输入顾客数:" << endl;
cin >> cusNum;
cout << "输入服务时间下界和上界(单位:分钟)" << endl;
cin >> sTMin >> sTMax;
cout << "输入到达时间下界和上界(单位:分钟)" << endl;
cin >> arL >> arH;
simulator MySim(sTMax, sTMin, cusNum, serNum,arL,arH);
MySim.Simulation();
return 0;
}