如果还未学习强连通分量,建议先学习强连通分量的tarjan算法强连通分量(tarjan算法)
1,定义
相对于在单向图的强连通分量,双连通分量是在无向图中,无向图有一个特点,可以以任何一个点为根节点建dfs树
割边(桥):删去一条边,会增加图中的强连通分量(即可以使原来连通的部分变成两半(不连通))
割点 :同理割边,不过是删边
如果删去一条边,仍然无法使不连通,说明是边双连通,点就是点双连通
边,点写法几乎一致,此处介绍边双连通
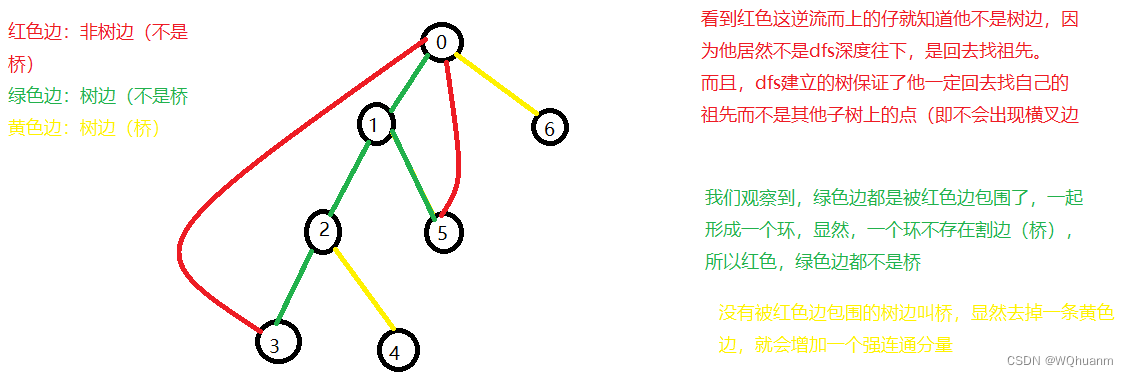
2,算法思路
其实与强连通分量的tarjan算法几乎没差
1,dfs树不断遍历点,不需要出栈,只入栈,不需要instack【】数组
2,因此我们如果遇到一个已经遍历过的点,毫无疑问,他是当前子树的祖先
3,因为是无向图,如果u与v之间有两条边(或以上)(就是说他们双连通),那么实际我们建边是建了4条,因为我们建的有向边*2,所以对于第二条边,我们需要flag来判定是否属于重边
4,因为dfs建树,需要判定父节点操作,多了个fa变量
void tarjan(int u, int fa)
{
dfn[u] = low[u] = ++dfncnt;
sta[++top] = u;
bool flag = 1;//判断重边
for (int i = head[u]; i; i = edge[i].next)
{
int v = edge[i].to;
if (v == fa && flag)//第一次v是父节点,只是因为无向边建边原因,直接跳过
{
flag = 0;
continue;
}//后面再遇到父节点,说明u与v确实不止一条无向边
if (!dfn[v])//没访问过,操作还是那样
{
tarjan(v, u);
low[u] = min(low[v], low[u]);
}
else low[u] = min(low[u], dfn[v]);//访问过,那绝对是找到祖先了,非树边——,找到一个强连通分量(环)了
}
if (low[u] == dfn[u])
{
++cnt;
sum[cnt] = 0;
while (1)
{
int v = sta[top--];
bcc[v] = cnt;
sum[cnt] += a[v];
if (u == v)break;
}
}
}3,练习:考研路茫茫——空调教室
思路:
就是把无向图缩点变成只有割边的图,然后变量树,走树状dp
#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 1e4 + 10;
int dfn[N], low[N], sta[N], bcc[N], head[N], hd[N], a[N];
ll sum[N], dp[N], ans, summ;
int num, num1, dfncnt, cnt, top;
struct node
{
int to, next;
} edge[N << 2], eg[N << 2]; //双向边要两倍的(N*2),所以N<<2
void init()
{
num = num1 = top = cnt = dfncnt = summ = 0;
ans = llINF;
memset(head, 0, sizeof(head));
memset(hd, 0, sizeof(hd));
memset(dfn, 0, sizeof(dfn));
}
void add(int u, int v)
{
edge[++num].next = head[u];
edge[num].to = v;
head[u] = num;
}
void add1(int u, int v)
{
eg[++num1].next = hd[u];
eg[num1].to = v;
hd[u] = num1;
}
void tarjan(int u, int fa)
{
dfn[u] = low[u] = ++dfncnt;
sta[++top] = u;
bool flag = 1;//判断重边
for (int i = head[u]; i; i = edge[i].next)
{
int v = edge[i].to;
if (v == fa && flag)//第一次v是父节点,只是因为无向边建边原因,直接跳过
{
flag = 0;
continue;
}//后面再遇到父节点,说明u与v确实不止一条无向边
if (!dfn[v])//没访问过,操作还是那样
{
tarjan(v, u);
low[u] = min(low[v], low[u]);
}
else low[u] = min(low[u], dfn[v]);//访问过,那绝对是找到祖先了,非树边——,找到一个强连通分量(环)了
}
if (low[u] == dfn[u])
{
++cnt;
sum[cnt] = 0;//sum存储这个环的总人数
while (1)
{
int v = sta[top--];
bcc[v] = cnt;
sum[cnt] += a[v];
if (u == v)break;
}
}
}
void dfs(int u, int fa)//我们如果割去一条边,对于摘掉一颗子树,所以每次取次必须是整个子树的值
{
dp[u] = sum[u];//dp先取子树根节点的值,区别sum与dp,dp是整颗树人数和,sum只是这个点的人数
for (int i = hd[u]; i; i = eg[i].next)//求这颗树的值,对于这颗树的顶点值加这子树的子树值的和(继续深入)
{
int v = eg[i].to;
if (v != fa)//深入,不能返祖
{
dfs(v, u);
dp[u] += dp[v];
}
}
ans = min(ans, abs(summ - 2 * dp[u]));//求完整个树才来比较,最优解,就是(总人数-2*当前分开人数)的最小
}
int main()
{ std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, m, x, y;
while (cin >> n >> m)
{
init();
for (int i = 1; i <= n; ++i)cin >> a[i], summ += a[i];//summ存整个图总人数
for (int i = 1; i <= m; ++i)cin >> x >> y, add(x + 1, y + 1), add(y + 1, x + 1);//双向边
for (int i = 1; i <= n; ++i)if (!dfn[i])tarjan(i, 0);
if (cnt == 1)
{
cout << "impossible" << endl;
}
else
{
for (int i = 1; i <= n; ++i)//缩点后重新建边
{
int u = bcc[i];
for (int j = head[i]; j; j = edge[j].next)
{
int v = bcc[edge[j].to];
if (u != v)add1(u, v);//不用特意建(v,u),后面遍历会有的
}
}
dfs(1, 0);//遍历dfs树
cout << ans << endl;
}
}
return 0;
}