3D-GS 与 Nerf 和 Gaussian Splatting

3D Gaussian Splatting for Real-Time Radiance Field Rendering

论文：link
code:link

video:link

1. 开山之作 Nerf

一切的开始都是起源于 NERF 开山之作 这里由详细的学习与拆解
【NERF】入门学习整理（一）

【NERF】入门学习整理（二）

【NERF】入门学习整理（三）

【NeRF数据集】LLFF格式数据集处理colmap结果记录

基于上面的了解，这个模型的输入:是一个五维的相机位姿（x,y,z,Yaw,Pitch）；输出：4D(R G B 不透明度)；
那这个模型有啥缺点和优点呢？

逼真的渲染效果： NERF 可以生成逼真的图像和视频，与真实照片和视频难以区分。
灵活性和可扩展性： NERF 可以用于渲染各种形状和大小的 3D 场景，包括室内和室外场景。
易于使用： NERF 只需要少量数据即可训练，并且可以使用标准的硬件进行训练和推理。

缺点包括：

计算成本高： NERF 的训练和推理过程需要大量的计算资源。
数据需求： NERF 需要大量的数据才能训练出高质量的模型。
泛化能力差： NERF 模型通常只适用于训练数据所代表的场景。
以下是 NERF 算法的一些具体应用：

虚拟现实和增强现实： NERF 可以用于创建逼真的虚拟环境和增强现实体验。
3D 建模： NERF 可以用于从照片或视频中生成 3D 模型。
逆向渲染： NERF 可以用于从图像或视频中恢复 3D 场景的几何形状和材质。
以下是 NERF 算法的一些研究方向：

提高计算效率： 研究人员正在开发更有效的 NERF 训练和推理算法。
提高数据效率： 研究人员正在开发能够从少量数据中学习的 NERF 模型。
提高泛化能力： 研究人员正在开发能够泛化到新场景的 NERF 模型。
总体而言，NERF 是一种具有巨大潜力的 3D 表示和渲染技术。随着研究的不断深入，NERF 算法将有望在更多的领域得到应用。

此外，NERF 还存在一些潜在的风险和挑战，包括：

模型偏见： NERF 模型可能会受到训练数据的偏见影响，从而导致生成不准确或偏颇的结果。
滥用风险： NERF 技术可能会被滥用来生成虚假信息或宣传材料。

2. 扛鼎之作 3D Gaussian Splatting

3D Gaussian Splatting是最近NeRF方面的突破性工作，它的特点在于重建质量高的情况下还能接入传统光栅化，优化速度也快（能够在较少的训练时间，实现SOTA级别的NeRF的实时渲染效果，且可以以 1080p 分辨率进行高质量的实时（≥ 30 fps）新视图合成）。开山之作就是论文“3D Gaussian Splatting for Real-Time Radiance Field Rendering”是2023年SIGGRAPH最佳论文。

首先，3DGS可以认为是NeRF的一种，做的任务也是新视图的合成。

对于NeRF而言，它属于隐式几何表达（Implicit Geometry ），这里我们在上面的【NERF】入门学习整理系列已经有了更加完整的百表达和分析；顾名思义，不表达点的具体位置，而表示点与点的关系。通过选取空间坐标作为采样点输入，隐式场景将输出这些点的几何密度是多少，颜色是什么。而所谓的神经隐式几何则是用神经网络转换上述输入输出的方法（输入三维空间坐标和观测视角，输出对应点的几何密度和颜色）。把光线上的一系列采样点加权积起来就渲染得到一个像素颜色，这便是NeRF神经辐射场渲染的流程。

此外，何的隐式表达可以分为体积类表达和表面类表达两种：

体积类表达：NeRF 属于体积类表达，通过几何密度决定采样点颜色的贡献度。
表面类表达：在表面类表达方式中，输入采样点，符号距离函数 SDF 输出空间中距离该点最近的表面的距离，正值表示表面外，负值表示表面内，表面类方法判定越靠近表面的采样点颜色贡献度越高。
既然有隐式，那么就有显式几何表达（ Explicit geometry），就是类似点云、三角mesh这类可以沿着存储空间遍历所有元素。（通过某些方式，真正的把物体上的点都表示出来）

对于渲染，NeRF是非常典型的backward mapping过程，即计算出每个像素点受到每个体素影响的方式来生成最终图像，对每个像素，投出一条视线，并累积其颜色和不透明度
而3DGaussian Splatting是forward mapping的过程，将每个体素视作一个模糊的球，投影到屏幕上。在Splatting中，我们计算出每个体素如何影响每个像素点.

2.1 什么是3D高斯？高斯由1D推广到3D的数学推导

对于高常说的高斯函数，其实是1D的高斯，也就是正态分布：
$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
其中：

μ 是正态分布的 均值，代表数据中心的位置。
σ 是正态分布的 标准差，代表数据离散程度。

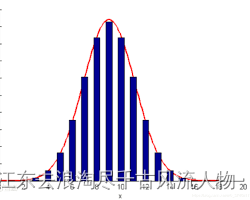
对于一段x区间,进行积分可以得到分布中的数据落在这一-区间的概率,其中绝大多数落在3sigma区域(概率是0.9974)。因此,一组 $mu$ 和$/sigma$ 可以确定一个1D高斯分布函数,进而确定一条1D线段通过改变这两个值就可以表达1D数轴上的一根线段。类似地,将这个思路从1D拓展到3D,那么就可以确定一个空间的椭球形,这个椭球分别以xyz轴对称,
从对称轴的垂直面切出来的横截面都是椭圆。不过由于这个椭球可以旋转移动,所以它的xyz对称轴不一定和世界坐标系重叠。对于标准的3DGaussians标准形式,是:
$$\begin{array}{c}G(x)=\sqrt{2\pi {\sigma }^2}\end{array}$$