一、题目
1、题目描述
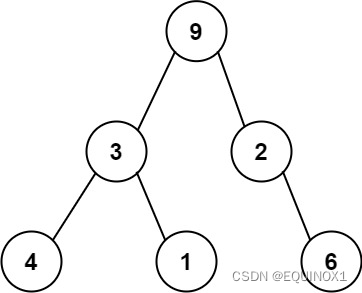
序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如
#。例如,上面的二叉树可以被序列化为字符串
"9,3,4,#,#,1,#,#,2,#,6,#,#",其中#代表一个空节点。给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
保证 每个以逗号分隔的字符或为一个整数或为一个表示
null指针的'#'。你可以认为输入格式总是有效的
- 例如它永远不会包含两个连续的逗号,比如
"1,,3"。注意:不允许重建树。
2、接口描述
class Solution {
public:
bool isValidSerialization(string preorder) {
}
};3、原题链接
331. 验证二叉树的前序序列化
二、解题报告
1、思路分析
一个非空节点可以产生两个位置,空节点和非空节点都会消耗一个位置
遍历序列,维护当前可用位置,如果可用位置为0,那么返回false
结束后,如果可用位置为0,那么返回true
2、复杂度
时间复杂度: O(n)空间复杂度:O(1)
3、代码详解
cpp
class Solution {
public:
bool isValidSerialization(string preorder) {
int s = 1;
for(int i = 0, n = preorder.size(); i < n; ){
if(s == 0) return false;
if(preorder[i] == ',') i++;
else if(preorder[i] == '#') s--, i++;
else {
while(i < n && preorder[i] != ',') i++;
s++;
}
}
return s == 0;
}
};python3
class Solution:
def isValidSerialization(self, preorder: str) -> bool:
n, i, s = len(preorder), 0, 1
while i < n:
if not s:
return False
elif preorder[i] == ',':
i += 1
elif preorder[i] == '#':
s -= 1
i += 1
else:
while i < n and preorder[i] != ',':
i += 1
s += 1
return s == 0