✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。
我是Srlua小谢,在这里我会分享我的知识和经验。🎥
希望在这里,我们能一起探索IT世界的奥妙,提升我们的技能。🔮
记得先点赞👍后阅读哦~ 👏👏
📘📚 所属专栏:
欢迎访问我的主页:Srlua小谢 获取更多信息和资源。✨✨🌙🌙

目录
数据链路层
数据链路层使用的信道
数据链路层的简单模型
使用点对点信道的数据链路层
数据链路和帧
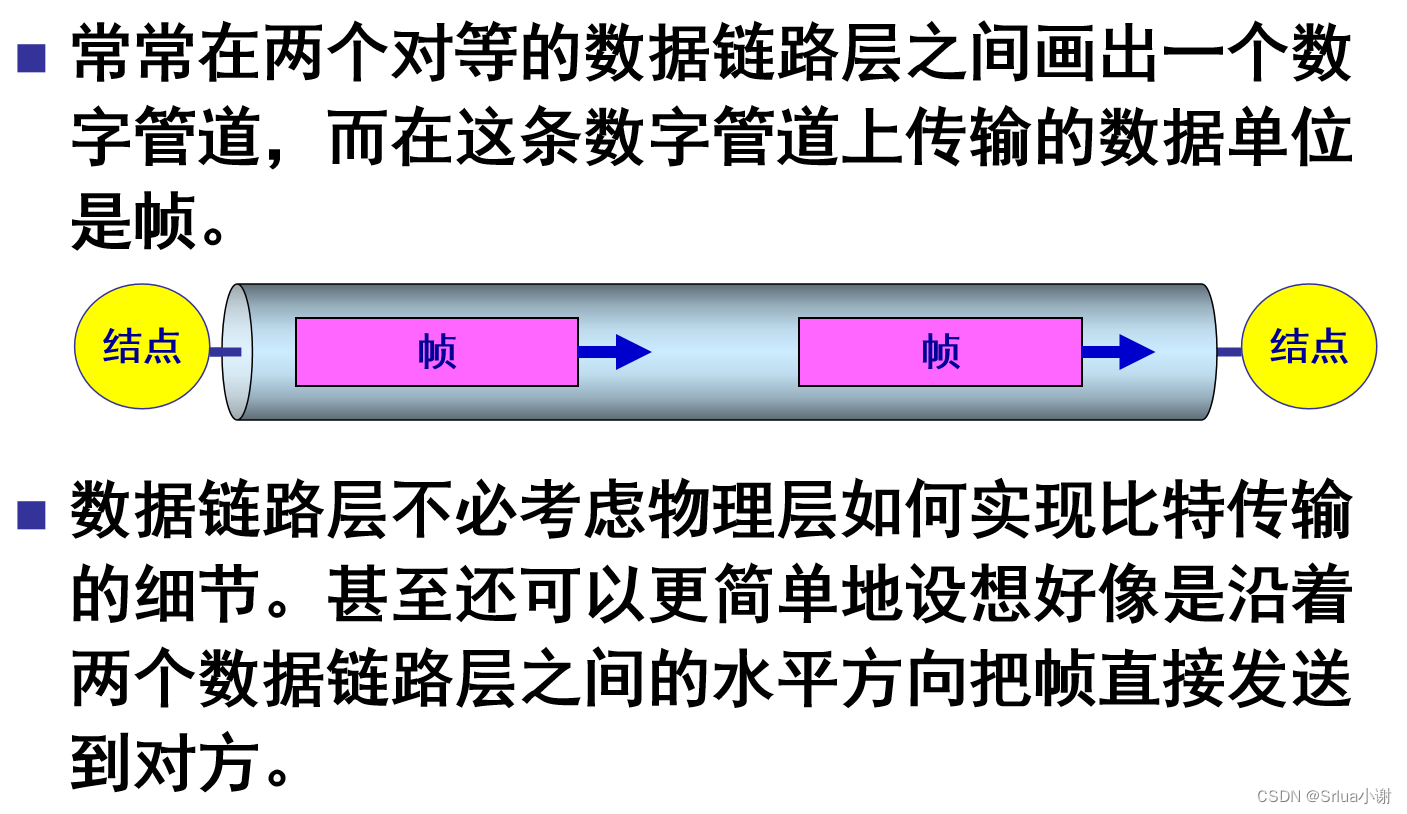
数据链路层像个数字管道
三个基本问题
1. 封装成帧
2. 透明传输
3. 差错控制
帧检验序列 FCS
接收端对收到的每一帧进行 CRC 检验
应当注意
数据链路层
数据链路层使用的信道
数据链路层使用的信道主要有以下两种类型:
点对点信道。这种信道使用一对一的点对点通信方式。
广播信道。这种信道使用一对多的广播通信方式,因此过程比较复杂。广播信道上连接的主机很多,因此必须使用专用的共享信道协议来协调这些主机的数据发送。
数据链路层的简单模型
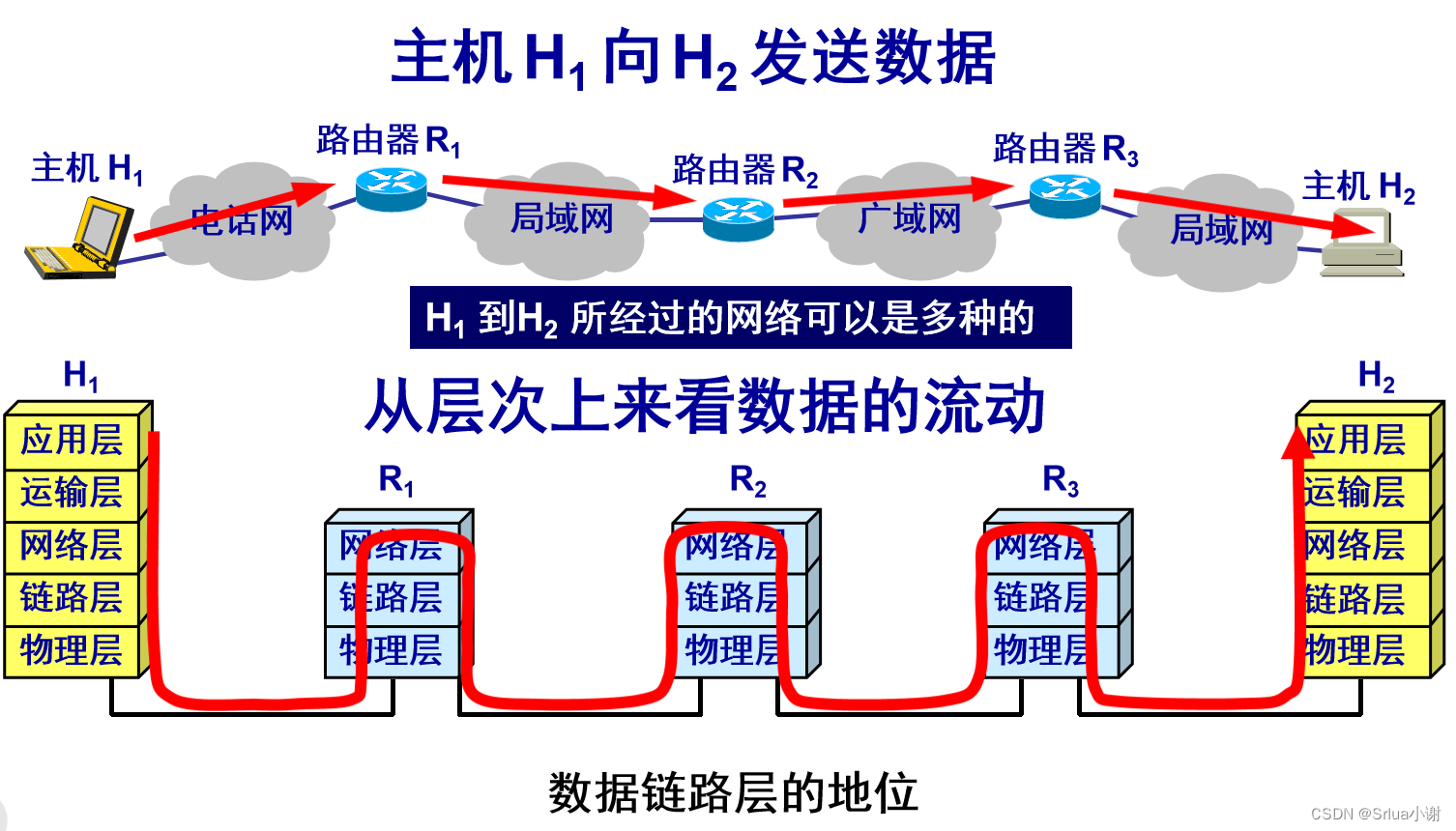

使用点对点信道的数据链路层
数据链路和帧
链路 (link) 是一条无源的点到点的物理线路段,中间没有任何其他的交换结点。
- 一条链路只是一条通路的一个组成部分。
数据链路 (data link) 除了物理线路外,还必须有通信协议来控制这些数据的传输。若把实现这些协议的硬件和软件加到链路上,就构成了数据链路。
- 现在最常用的方法是使用适配器(即网卡)来实现这些协议的硬件和软件。
- 一般的适配器都包括了数据链路层和物理层这两层的功能。
也有人采用另外的术语。这就是把链路分为物理链路和逻辑链路。
物理链路就是上面所说的链路。
逻辑链路就是上面的数据链路,是物理链路加上必要的通信协议。
早期的数据通信协议曾叫做通信规程 (procedure)。因此在数据链路层,规程和协议是同义语。

数据链路层像个数字管道
三个基本问题
数据链路层协议有许多种,但有三个基本问题则是共同的。
这三个基本问题是:
1. 封装成帧
封装成帧 (framing) 就是在一段数据的前后分别添加首部和尾部,然后就构成了一个帧。确定帧的界限。 首部和尾部的一个重要作用就是进行帧定界。
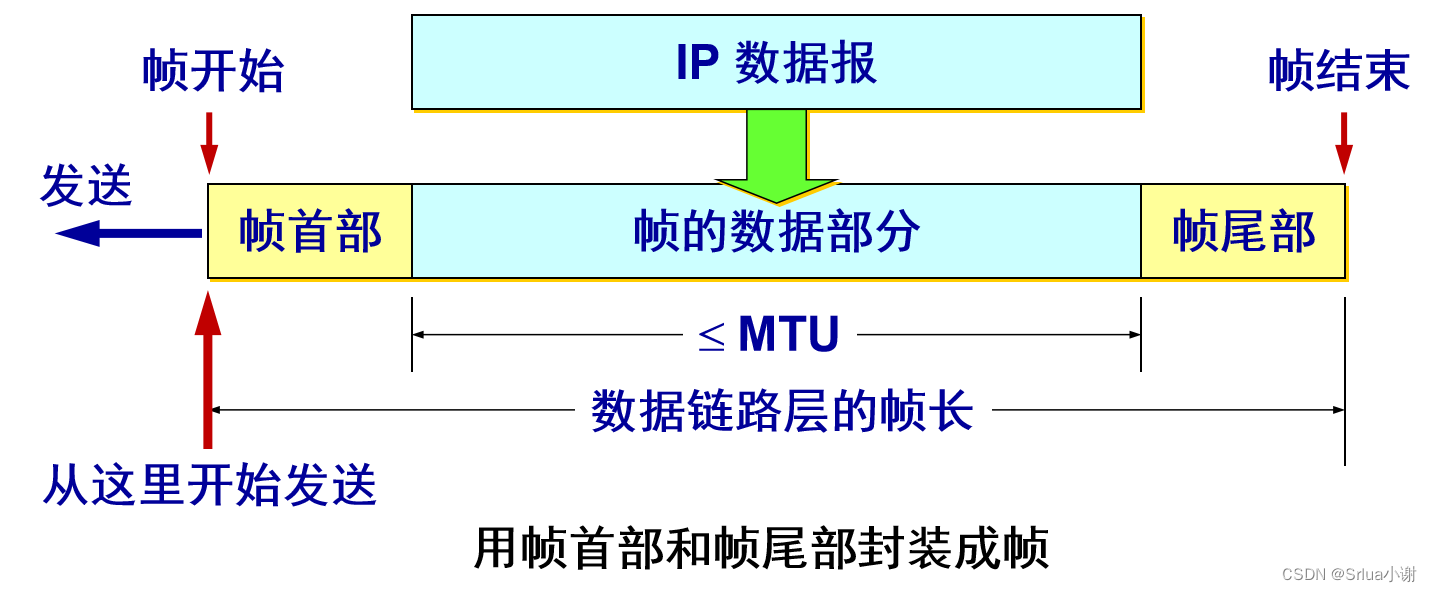 用控制字符进行帧定界的方法举例
用控制字符进行帧定界的方法举例
当数据是由可打印的 ASCII 码组成的文本文件时,帧定界可以使用特殊的帧定界符。
控制字符 SOH (Start Of Header) 放在一帧的最前面,表示帧的首部开始。另一个控制字符 EOT (End Of Transmission) 表示帧的结束。
 2. 透明传输
2. 透明传输
如果数据中的某个字节的二进制代码恰好和 SOH 或 EOT 一样,数据链路层就会错误地“找到帧的边界”。
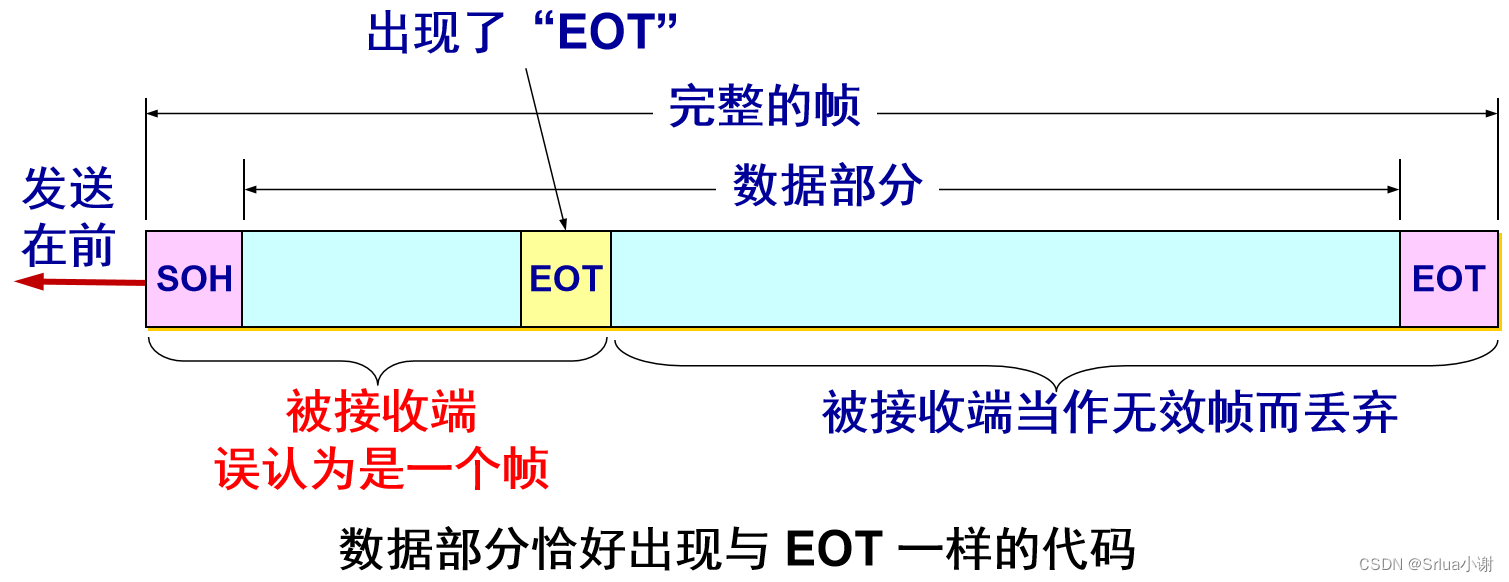
解决透明传输问题
解决方法:字节填充 (byte stuffing) 或字符填充 (character stuffing)。
- 发送端的数据链路层在数据中出现控制字符“SOH”或“EOT”的前面插入一个转义字符“ESC” (其十六进制编码是 1B)。
- 接收端的数据链路层在将数据送往网络层之前删除插入的转义字符。
- 如果转义字符也出现在数据当中,那么应在转义字符前面插入一个转义字符 ESC。当接收端收到连续的两个转义字符时,就删除其中前面的一个。
用字节填充法解决透明传输的问题
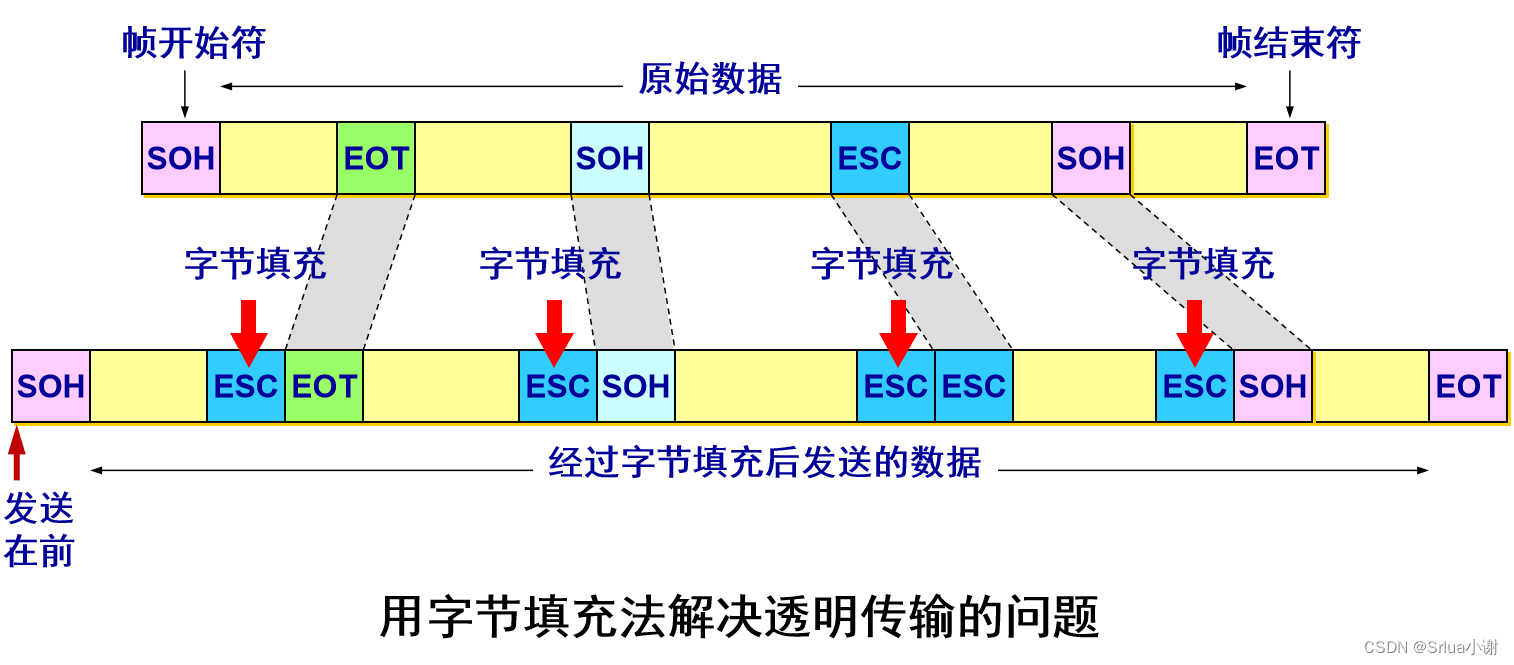 3. 差错控制
3. 差错控制
在传输过程中可能会产生比特差错:1 可能会变成 0 而 0 也可能变成 1。
在一段时间内,传输错误的比特占所传输比特总数的比率称为误码率 BER (Bit Error Rate)。
误码率与信噪比有很大的关系。
为了保证数据传输的可靠性,在计算机网络传输数据时,必须采用各种差错检测措施。
循环冗余检验的原理
在数据链路层传送的帧中,广泛使用了循环冗余检验 CRC 的检错技术。
在发送端,先把数据划分为组。假定每组 k 个比特。
假设待传送的一组数据 M = 101001(现在 k = 6)。我们在 M 的后面再添加供差错检测用的 n 位冗余码一起发送。
冗余码的计算
用二进制的模 2 运算进行 2n 乘 M 的运算,这相当于在 M 后面添加 n 个 0。
得到的 (k + n) 位的数除以事先选定好的长度为 (n + 1) 位的除数 P,得出商是 Q 而余数是 R,余数 R 比除数 P 少 1 位,即 R 是 n 位。
将余数 R 作为冗余码拼接在数据 M 后面发送出去。
冗余码的计算举例
现在 k = 6, M = 101001。
设 n = 3, 除数 P = 1101, 被除数是 2nM = 101001000。
模 2 运算的结果是:商 Q = 110101,余数 R = 001。
把余数 R 作为冗余码添加在数据 M 的后面发送出去。发送的数据是:2nM + R
即:101001001,共 (k + n) 位。
循环冗余检验的原理说明

帧检验序列 FCS
在数据后面添加上的冗余码称为帧检验序列 FCS (Frame Check Sequence)。
循环冗余检验 CRC 和帧检验序列 FCS 并不等同。
- CRC 是一种常用的检错方法,而 FCS 是添加在数据后面的冗余码。
- FCS 可以用 CRC 这种方法得出,但 CRC 并非用来获得 FCS 的唯一方法。
接收端对收到的每一帧进行 CRC 检验
(1) 若得出的余数 R = 0,则判定这个帧没有差错,就接受 (accept)。
(2) 若余数 R 0,则判定这个帧有差错,就丢弃。
但这种检测方法并不能确定究竟是哪一个或哪几个比特出现了差错。
只要经过严格的挑选,并使用位数足够多的除数 P,那么出现检测不到的差错的概率就很小很小。
应当注意
仅用循环冗余检验 CRC 差错检测技术只能做到无差错接受 (accept)。
“无差错接受”是指:“凡是接受的帧(即不包括丢弃的帧),我们都能以非常接近于 1 的概率认为这些帧在传输过程中没有产生差错”。
也就是说:“凡是接收端数据链路层接受的帧都没有传输差错”(有差错的帧就丢弃而不接受)。
要做到“可靠传输”(即发送什么就收到什么)就必须再加上确认和重传机制。
应当明确,“无比特差错”与“无传输差错”是不同的概念。
在数据链路层使用 CRC 检验,能够实现无比特差错的传输,但这还不是可靠传输。
本文介绍的数据链路层协议都不是可靠传输的协议。

希望对你有帮助!加油!
若您认为本文内容有益,请不吝赐予赞同并订阅,以便持续接收有价值的信息。衷心感谢您的关注和支持!