| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
文章目录
- 广度优先+双分裂蛇
广度优先+双分裂蛇
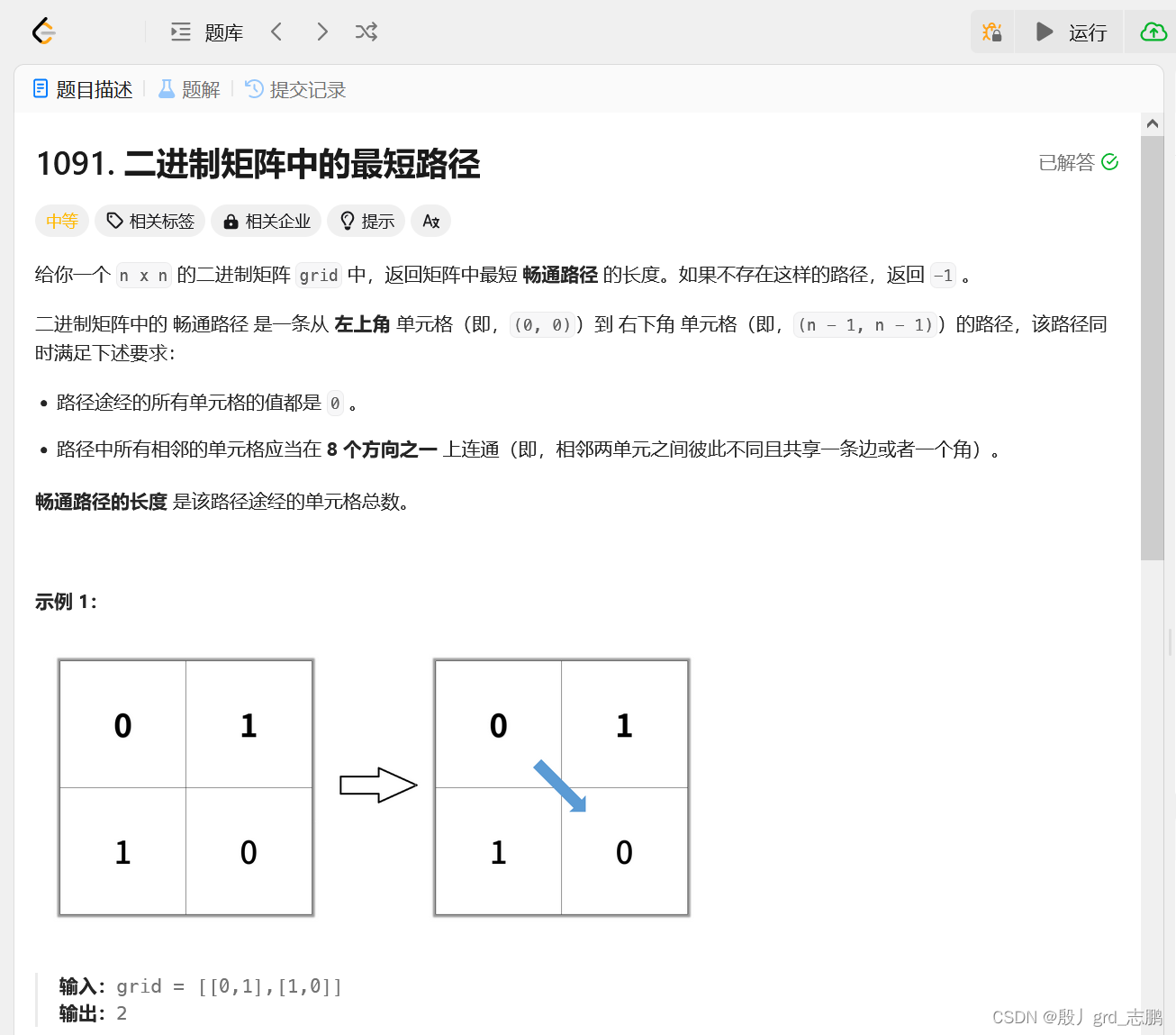
双分裂蛇:是求二维表中从起点到终点的经典思路(也是求无权图的最短路径问题的经典解法)。创建两条分裂蛇,分别从起点和终点出发,两者相遇,则找到一条路径。时间复杂度理论上和单分裂蛇一样,但实际效率双分裂蛇更高。
- 分裂蛇的意思是:如果遇到分叉路,分裂蛇A可以分裂成对应数量的蛇,然后分头行动。
- 为什么双分裂蛇更快?因为只有一条蛇时,最坏情况下所有结点都走一遍才能找到最短路径
- 而
双分裂蛇,无论分裂多少,肯定是最短路径上的两条蛇最先相遇。所以两条蛇初次相遇的路径,就是最短路径。而不用像单分裂蛇那样,很有可能将所有路走一遍再比较才能知道哪条路最短。简单来说,单分裂蛇,它需要走的步数更多,因为它要自己从起点走到终点,因此分裂的蛇也就越多,访问的结点也就越多。
而双分裂蛇,两条蛇走的步数都是单分裂蛇的一半。所以两条蛇分裂的蛇会很少。访问的结点就少举个例子,一张可以无限对折的0.0002米厚的纸,对折40次左右可以到月球,40次正好就是219902公里。而对折40次的一半左右,比如23次只有1.677公里。此时我搞两张纸各对折40次的一半,加起来是1.677+1.677 = 3.3公里左右
可见,
219902公里是一张纸对折40次的结果。3.3公里左右是两张纸对折40次一半20次左右的结果. 而回到分裂蛇的例子。一条蛇分裂40次,和两条蛇各分裂20次。谁访问的结点更少呢?
因此理论上,最坏情况下双分裂蛇和单分裂蛇都是n^2的时间复杂度,也就是每个结点访问两次,但是实际上,找最短路径,就和一张纸对折40次和两张纸对折20次的区别是一样的,只要路径足够长,双分裂蛇访问的结点个数,和单分裂蛇访问的结点个数根本不是一个量级,
就像一张纸对折40次上月球,两张纸对折20次加起来走不出一个小区是一个道理。双分裂蛇的效率是比单分裂蛇高的。
但是无论单分裂蛇还是双分裂蛇,找最短路径,都满足:初次相遇的蛇所在路径为最短路径。
也就是,就算是单分裂蛇,也不需要所有路径走一遍统计路径长度,才能找出最短的
因为最短路径上的蛇一定会先最先到达。(前提是所有蛇的速度一样,都是大家一起一步一步走)
| 解题思路:时间复杂度O( n 2 n^2 n2),空间复杂度O( n 2 n^2 n2) |
|---|
- 创建两个队列A和B,当做分裂蛇,分别从起点[0][0]和终点[n-1][n-1]出发,将两个结点分别入各自的队列
- A队列先走一步,情况允许就分裂。新分裂出的蛇
不额外走
- 一步的含义是,我可以向8个方向走,只要能走就走。
- 分裂:如果多个方向都满足条件,则进行分裂,让分裂的蛇到达指定地点(一步),
然后将分裂的蛇全部入队列- 但是新入队列的蛇,不可以继续处理,因为它们已经走了一步了
- 如果两个队列没有相遇,B队列也走一步,情况允许就分裂,新分裂的不走
- 直到两个队列中有蛇相遇,就结束程序。因为双分裂蛇的特点就是,最先相遇的两条蛇所在路径为最短路径
| 代码:会给出双分裂蛇和单分裂蛇的两版代码,除了蛇的数量不一样,剩余代码全部一样,可以很明显的看见,双分裂蛇的效率高多了,比单分裂蛇效率高了40% |
|---|
- 双分裂蛇版本用时6ms
class Solution {
final static int[] dx = {1, 1, 1, 0, 0, -1, -1, -1};//右下,下,左下,右,左,右上,上,左上
final static int[] dy = {1, 0, -1, 1, -1, 1, 0, -1};//右下,下,左下,右,左,右上,上,左上
final static int SIGN_A = 2;//A队列走过的路的标识
final static int SIGN_B = 3;//B队列走过的路的标识
class Node {//队列中的结点,保存x和y坐标
int x, y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
}
public int shortestPathBinaryMatrix(int[][] grid) {
int n = grid.length;
if(grid[0][0] == 1 || grid[n-1][n-1] == 1) return -1;
else if(grid[0][0] == 0 && n == 1) return 1;
int steps = 2;//走了多少步,两个队列(贪吃蛇)一起算
//头尾队列,一个从头走,一个从尾巴走,两个队列相遇,就是一个答案
Queue<Node> headQue = new LinkedList<Node>();
Queue<Node> tailQue = new LinkedList<Node>();
headQue.offer(new Node(0, 0));
tailQue.offer(new Node(n-1, n-1));
grid[0][0] = SIGN_A;
grid[n-1][n-1] = SIGN_B;
//两个队列一起走
while(!headQue.isEmpty() && !tailQue.isEmpty()) {
boolean encounter = nextStep(grid, headQue, SIGN_A);//A队列走一步,是否相遇B队列
if(encounter) return steps;//如果相遇,则返回步数
//没有相遇,则A队列步数+1
steps++;
//B队列走一步,是否相遇A队列
encounter = nextStep(grid, tailQue, SIGN_B);
if(encounter) return steps;
steps++;
}
return -1;//如果一直没有相遇就返回-1
}
//走一步
private boolean nextStep(int [][]grid, Queue<Node> que, int sign) {
int n = grid.length;
int size = que.size();
while((size--) > 0) {//如果当前队列有结点(无论多少个),那么这些结点只走一步,不多走,也就是这些结点走了一步后,过程中新添加的结点,本次不考虑
Node cur = que.poll();//出队列当前结点
int x = cur.x, y = cur.y;//获取其坐标
for(int i = 0; i < 8; ++i) {//8个方向按右下,下,左下,右,左,右上,上,左上的顺序走一下
int nx = x + dx[i];
int ny = y + dy[i];
//如果下标越界,或者要走的这一方向==1(此路不通),或者要走的这一方向当前队列已经走过了grid[nx][ny] == sign,就跳过
if(nx < 0 || nx >= n || ny < 0 || ny >= n || grid[nx][ny] == 1 || grid[nx][ny] == sign) continue;
// 如果要走的方向遇到了另一个队列,则说明相遇
if(grid[nx][ny] != 0) return true;//返回true
//如果没有相遇,向当前方向走一步
grid[nx][ny] = sign;
que.add(new Node(nx, ny));//添加到队列继续
}
}
return false;
}
}
- 单分裂蛇版本,用时10ms
class Solution {
public int shortestPathBinaryMatrix(int[][] grid) {
if(grid[0][0] != 0)return -1;
if(grid.length == 1){
if(grid[0][0] == 0) return 1;
else return -1;
}
int[] dx = {-1, -1, -1, 0, 0, 1, 1, 1};
int[] dy = {-1, 0, 1, -1, 1, -1, 0,1};
int n = grid.length;
// 记录坐标
Queue<int[]> queue = new LinkedList();//单分裂蛇
queue.offer(new int[]{0,0});//从起点开始
grid[0][0] = 1;//走过的就标志为1
int length = 0;//路径长度
loop:while(queue.size() > 0){//如果还有分裂蛇存在
int size = queue.size();//获取当前分裂蛇,这些分裂蛇可以进行分裂,然后走一步
++length;//走一步+1个路径长度
while((size--) > 0){//只有当前分裂蛇可以走一步,多条路可走就分裂,新的分裂蛇不可以走,如果使用queue.size()会将新的分裂蛇也处理了
int[] pos = queue.poll();//依次获取这些现在存在的分裂蛇
for(int i =0; i < 8; i++){//从8个方向走
int x = pos[0] + dx[i];
int y = pos[1] + dy[i];
//如果这个方向可以走,并且没有分裂蛇走过
if(x >=0 && y >= 0 && x < grid.length && y < grid.length && grid[x][y] == 0){
queue.offer(new int[]{x,y});//就分裂一条蛇过去,这条分裂后新进入队列的蛇,本次不可以再处理
grid[x][y] = length +1;//将此结点标志为已到达过,赋值为:路径长度+1
//这里很重要,终点一定是最短路径的蛇先到,此时它会将这个结点标志为已到访过
//后面在较长路径的蛇,不会覆盖这个值
//如果当前分裂蛇是第一个到终点的,则他就是最短路径上的蛇
if(x == grid.length-1 && y == grid.length-1) break loop;//跳出整个循环,不继续处理任何蛇
}
}
}
}
return grid[n-1][n-1] <2 ? -1 : grid[n-1][n-1];//返回到终点的最短路径长度
}
}