语音识别：基于HMM

news2024/11/24 16:25:45

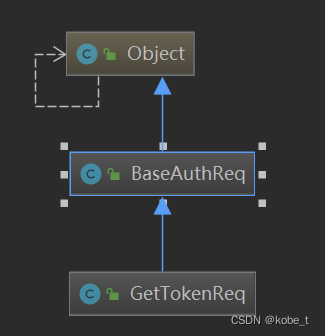
HMM语音识别的解码过程

从麦克风采集的输入音频波形被转换为固定尺寸的一组声学向量：

$\mathbf{Y}_{1:T} = \mathbf{y}_{1}, \mathbf{y}_{2}, ..., \mathbf{y}_{T}$

其中 $\mathbf{y}_{t}, t=1,2, ...,T$ 是 $D$ 维的语音特征向量（例如MFCC）。

解码器尝试去找到上述特征向量序列对应的单词（word）的序列：

$\mathbf{w}_{1:L} = w_{1}, w_{2},...,w_{L}$

单词序列的长度是 $L$ 。

也即是解码器尝试寻找模型产生 $\mathbf{Y}$ 的那个最有可能的单词序列 $\mathbf{w}$ ：

$\widehat{\mathbf{w}} = \underset{\mathbf{w}}{arg max}{P(\mathbf{w} | \mathbf{Y})}$

经过贝叶斯公式：

$\widehat{\mathbf{w}} = \underset{\mathbf{w}}{arg max}\left \{ P(\mathbf{Y} | \mathbf{w}) P(\mathbf{w}) \right \}$

似然概率 $P(\mathbf{Y} | \mathbf{w})$ 是语音识别的声学模型，先验概率 $P(\mathbf{w})$ 是语音模型。

$P(\mathbf{Y}|\mathbf{w}) = \underset{\mathbf{Q}}{\sum_{}}P(\mathbf{Y|Q})P(\mathbf{Q}|\mathbf{w}))$

$\mathbf{Q} = \mathbf{q}^{(w_{1})}, \mathbf{q}^{(w_{2})}, ..., \mathbf{q}^{(w_{L})}$

$\mathbf{q}^{(w_{l})} = q_{1}, q_{2}, ...,q_{K_{w_{l}}}$ 是一个单词由基本音素组成的发音序列（也就是单词的音标），

$\mathbf{Q}$ 是该句子的一个可能发音序列，由该句子的每个单词的基本音素拼接而成。

这里的求和是使用了全概率公式，因为一个单词可能由多个发音，所以句子的发音序列也是多个。

对于该句子的一个可能发音序列 $\mathbf{Q}$ ，可得

$P(\mathbf{Q}|\mathbf{w}) = \prod_{l=1}^{L}P(\mathbf{q}^{(w_{l})}|w_{l})$

剩下就是计算 $P(\mathbf{Y|Q})$ 了。

$P(\mathbf{Y|Q}) = \underset{\mathbf{S} }{\sum}P(\mathbf{S}, \mathbf{Y} | \mathbf{Q})$

给定发音序列，对每一个可能的状态序列 $\mathbf{S}$ 求句子HMM的概率。

$\mathbf{S} = S_0, S_1, ... , S_{T+1}$ 是特征序列对应的一个候选的状态序列。

$P(\mathbf{S}, \mathbf{Y} | \mathbf{Q}) = a_{S_{0}S_{1}}\prod_{t=1}^{T}b_{S_{t}}(\mathbf{y}_t)a_{S_{t}S_{t+1}}$

解码过程不需要计算所有可能状态序列的似然概率，我们只需要使用维特比（Viterbi）算法获取概率最大的那个状态序列路径。

$P^{*}(\mathbf{Y}|\mathbf{Q}, \lambda ) = \underset{\mathbf{S}}{max}P(\mathbf{S}, \mathbf{Y}|\mathbf{Q}, \lambda )$

模型参数：

HMM语音识别声学模型的训练过程（单音素）

$R$ 个语料片段，每个语料片段对应的特征向量序列为 $\mathbf{Y}^{(r)},r = 1, 2, ..., R$ ， $\mathbf{Y}^{(r)}$ 序列的长度为 $T^{(r)}$ ，

HMM的训练（选择正确的参数）意味着：找到模型的参数（如转移概率和发射概率），使得给定的所有输入语料 $\mathbf{Y}^{(r)},r = 1, 2, ..., R$ 的概率最大：

关于 $\lambda$ ，

$Maximize \sum_{r=0}^{R}\underset{\mathbf{S}}{\sum }p(\mathbf{Y}^{(r)}, \mathbf{S}|\lambda )$

E-step

前向概率：

$\alpha _{t}^{(rj)} = P(\mathbf{Y}_{1:t}^{(r)}, S_{t} = j;\lambda )$

即对 $\mathbf{Y}^{(r)}$ 的前 $t$ 个特征向量与 $t$ 时刻的状态为 $j$ 的联合概率；

后向概率：

$\beta _{t}^{(rj)} = P(\mathbf{Y}_{t+1:T^{(r)}}^{(r)},|S_{t} = i;\lambda )$

给定 $t$ 时刻的状态为 $i$ ，模型生成 $t$ +1到 $T^{(r)}$ 之间的特征向量序列的条件概率。

给定前向和向后的概率，对于任何给定的语料 $r$ ，模型在时间 $t$ 时占据状态 $j$ 的概率是

其中， $P^{r} = p(Y^{(r)};\lambda )$ 可通过前向概率或者后向概率的递推公式获得，等于 $t = T^{(r)}+1$ 时刻的前向概率，也等于 $t = 0$ 时刻的后向概率。

M-step

对于所有的语料，给定初始的模型参数 $\lambda _{0}$ （均值，方差，转移概率），可通过如下的公式迭代参数

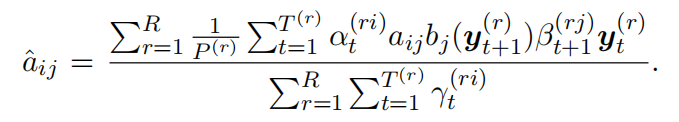
注意，这里使用的是单个高斯分布建模观察概率 $b_{j}(\mathbf{y}_{t}^{(r)}) = N(\mathbf{y}_{t}^{(r)}, \mu _{j}, \Sigma _{j})$ 而不是GMM。

Kaldi中使用的HMM声学模型训练方法

因为转移概率对识别结果的影响很小，甚至有时候可以忽略。Kaldi中一般是将转移概率固定不变，不在训练中更新转移概率。声学模型包含的信息主要是状态定义和各个状态的观察概率（发射概率）分布。

使用从左到右的线性HMM模型结构（只有向右跳转和自跳转），训练过程中只更新每个状态的高斯混合模型（GMM）参数。

上面介绍的HMM训练方法是经典的训练HMM的方法(baum welch算法)，该算法就是在给定一个初始的模型参数，通过不断的E-step，M-step迭代模型的参数。一种更加实际的方法是使用Viterbi训练方法：

1、给定初始的参数 $\lambda^{0}$

2、使用维特比算法和当前的参数 $\lambda ^{k}$ 找到能够解释 $\mathbf{Y}^{(r)}, r = 1, 2,..., R$ 的最可能的状态序列 $\mathbf{Z}^{*}$ ，这样就得到了每一帧 $\mathbf{y}^{(r)}_{t}$ 对应的状态。这个过程也叫做对齐（Align）或者强制对齐（Forced alignment），目的是获取每一帧对应的状态。

3、使用统计公式更新模型的参数 $\lambda ^{k+1}$ 。因为此时已经有大量已知隐藏状态和特征（观察值）的帧，所以可以更新每个状态对应的发射概率分布（GMM）的均值和协方差以及权重等参数（可能会用到GMM的EM算法估计GMM的参数）

4、重复步骤2、3，直到状态序列不再更新（收敛）。

参考：

[1] Gales and Young (2007). “The Application of Hidden Markov Models in Speech Recognition”, Foundations and Trends in Signal Processing , 1 (3), 195–304: section 2.2.\

[2]《Kaldi语音识别实战》

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1557901.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！