1,原理
通过雅可比旋转,对对称矩阵计算特征值和特征向量;
通过初等正交变换,每次把其中一个非主对角元素消成零,最终只剩主对角线非零元素为特征值,同时把初等变换累积下来,构成特征向量。
2,源码
yevj.cpp
计算一个512 阶的矩阵的特征值和特征向量:
#include <hip/hip_runtime.h>
#include <hipsolver/hipsolver.h>
#include <iostream>
#include <random>
#include <vector>
#include <functional>
#include <sstream>
#include <stdexcept>
#include <string>
#define NA 512
#define PR_D 0
constexpr int error_exit_code = -1;
inline int report_validation_result(int errors)
{
if(errors)
{
std::cout << "Validation failed. Errors: " << errors << std::endl;
return error_exit_code;
}
std::cout << "Validation passed." << std::endl;
return 0;
}
template<typename T>
void multiply_matrices(T alpha,
T beta,
int m,
int n,
int k,
const T* A,
int stride1_a,
int stride2_a,
const T* B,
int stride1_b,
int stride2_b,
T* C,
int stride_c)
{
for(int i1 = 0; i1 < m; ++i1)
{
for(int i2 = 0; i2 < n; ++i2)
{
T t = T(0.0);
for(int i3 = 0; i3 < k; ++i3)
{
t += A[i1 * stride1_a + i3 * stride2_a] * B[i3 * stride1_b + i2 * stride2_b];
}
C[i1 + i2 * stride_c] = beta * C[i1 + i2 * stride_c] + alpha * t;
}
}
}
template<class BidirectionalIterator>
inline std::string format_range(const BidirectionalIterator begin, const BidirectionalIterator end)
{
std::stringstream sstream;
sstream << "[ ";
for(auto it = begin; it != end; ++it)
{
sstream << *it;
if(it != std::prev(end))
{
sstream << ", ";
}
}
sstream << " ]";
return sstream.str();
}
inline const char* hipsolverStatusToString(hipsolverStatus_t status)
{
switch(status)
{
case HIPSOLVER_STATUS_SUCCESS: return "HIPSOLVER_STATUS_SUCCESS";
case HIPSOLVER_STATUS_NOT_INITIALIZED: return "HIPSOLVER_STATUS_NOT_INITIALIZED";
case HIPSOLVER_STATUS_ALLOC_FAILED: return "HIPSOLVER_STATUS_ALLOC_FAILED";
case HIPSOLVER_STATUS_INVALID_VALUE: return "HIPSOLVER_STATUS_INVALID_VALUE";
case HIPSOLVER_STATUS_MAPPING_ERROR: return "HIPSOLVER_STATUS_MAPPING_ERROR";
case HIPSOLVER_STATUS_EXECUTION_FAILED: return "HIPSOLVER_STATUS_EXECUTION_FAILED";
case HIPSOLVER_STATUS_INTERNAL_ERROR: return "HIPSOLVER_STATUS_INTERNAL_ERROR";
case HIPSOLVER_STATUS_NOT_SUPPORTED: return "HIPSOLVER_STATUS_NOT_SUPPORTED";
case HIPSOLVER_STATUS_ARCH_MISMATCH: return "HIPSOLVER_STATUS_ARCH_MISMATCH";
case HIPSOLVER_STATUS_HANDLE_IS_NULLPTR: return "HIPSOLVER_STATUS_HANDLE_IS_NULLPTR";
case HIPSOLVER_STATUS_INVALID_ENUM: return "HIPSOLVER_STATUS_INVALID_ENUM";
case HIPSOLVER_STATUS_UNKNOWN: return "HIPSOLVER_STATUS_UNKNOWN";
#if (hipsolverVersionMajor == 1 && hipsolverVersionMinor >= 8) || hipsolverVersionMajor >= 2
case HIPSOLVER_STATUS_ZERO_PIVOT: return "HIPSOLVER_STATUS_ZERO_PIVOT";
#endif
}
// We don't use default so that the compiler warns if any valid enums are missing from the
// switch. If the value is not a valid hipsolverStatus_t, we return the following.
return "<undefined hipsolverStatus_t value>";
}
#define HIP_CHECK(condition) \
{ \
const hipError_t error = condition; \
if(error != hipSuccess) \
{ \
std::cerr << "An error encountered: \"" << hipGetErrorString(error) << "\" at " \
<< __FILE__ << ':' << __LINE__ << std::endl; \
std::exit(error_exit_code); \
} \
}
#define HIPSOLVER_CHECK(condition) \
{ \
const hipsolverStatus_t status = condition; \
if(status != HIPSOLVER_STATUS_SUCCESS) \
{ \
std::cerr << "hipSOLVER error encountered: \"" << hipsolverStatusToString(status) \
<< "\" at " << __FILE__ << ':' << __LINE__ << std::endl; \
std::exit(error_exit_code); \
} \
}
void init_matrix(std::vector<double> &A, int n, int lda)
{
std::default_random_engine generator;
std::uniform_real_distribution<double> distribution(0., 2.);
auto random_number = std::bind(distribution, generator);
for(int i = 0; i < n; i++)
{
A[(lda + 1) * i] = random_number();
for(int j = 0; j < i; j++)
{
A[i * lda + j] = A[j * lda + i] = random_number();
}
}
}
int main(const int argc, char* argv[])
{
int n = NA;
if(n <= 0)
{
std::cout << "Value of 'n' should be greater than 0" << std::endl;
return 0;
}
const int lda = n;
// 2. Data vectors
std::vector<double> A(n * lda); // Input matrix
std::vector<double> V(n * lda); // Resulting eigenvectors
std::vector<double> W(n); // resulting eigenvalues
// 3. Generate a random symmetric matrix
init_matrix(A, n, lda);
// 4. Set hipsolver parameters
const hipsolverEigMode_t jobz = HIPSOLVER_EIG_MODE_VECTOR;
const hipsolverFillMode_t uplo = HIPSOLVER_FILL_MODE_LOWER;
hipsolverSyevjInfo_t params;
HIPSOLVER_CHECK(hipsolverCreateSyevjInfo(¶ms));
HIPSOLVER_CHECK(hipsolverXsyevjSetMaxSweeps(params, 100));
HIPSOLVER_CHECK(hipsolverXsyevjSetTolerance(params, 1.e-7));
HIPSOLVER_CHECK(hipsolverXsyevjSetSortEig(params, 1));
// 5. Reserve and copy data to device
double* d_A = nullptr;
double* d_W = nullptr;
int* d_info = nullptr;
HIP_CHECK(hipMalloc(&d_A, sizeof(double) * A.size()));
HIP_CHECK(hipMalloc(&d_W, sizeof(double) * W.size()));
HIP_CHECK(hipMalloc(&d_info, sizeof(int)));
HIP_CHECK(hipMemcpy(d_A, A.data(), sizeof(double) * A.size(), hipMemcpyHostToDevice));
// 6. Initialize hipsolver
hipsolverHandle_t hipsolver_handle;
HIPSOLVER_CHECK(hipsolverCreate(&hipsolver_handle));
// 7. Get and reserve the working space on device.
int lwork = 0;
double* d_work = nullptr;
HIPSOLVER_CHECK(
hipsolverDsyevj_bufferSize(hipsolver_handle, jobz, uplo, n, d_A, lda, d_W, &lwork, params));
std::cout<< "LL:: 1 lwork = "<<lwork<<"bytes"<<std::endl;
lwork += 64;
// lwork = ((lwork+64-1)/64)*64;
std::cout<< "LL:: 2 lwork = "<<lwork<<"bytes"<<std::endl;
HIP_CHECK(hipMalloc(&d_work, sizeof(double) * lwork));
// 8. Compute eigenvectors and eigenvalues
HIPSOLVER_CHECK(hipsolverDsyevj(hipsolver_handle,
jobz,
uplo,
n,
d_A,
lda,
d_W,
d_work,
lwork,
d_info,
params));
// 9. Get results from host.
int info = 0;
HIP_CHECK(hipMemcpy(V.data(), d_A, sizeof(double) * V.size(), hipMemcpyDeviceToHost));
HIP_CHECK(hipMemcpy(W.data(), d_W, sizeof(double) * W.size(), hipMemcpyDeviceToHost));
HIP_CHECK(hipMemcpy(&info, d_info, sizeof(int), hipMemcpyDeviceToHost));
// 10. Print results
if(info == 0)
{
std::cout << "SYEVJ converges." << std::endl;
}
else if(info > 0)
{
std::cout << "SYEVJ does not converge (" << info << " elements did not converge)."
<< std::endl;
}
std::cout << "\nGiven the n x n square input matrix A; we computed the linearly independent "
"eigenvectors V and the associated eigenvalues W."
<< std::endl;
#if PR_D
std::cout << "A = " << format_range(A.begin(), A.end()) << std::endl;
std::cout << "W = " << format_range(W.begin(), W.end()) << std::endl;
std::cout << "V = " << format_range(V.begin(), V.end()) << std::endl;
#endif
int sweeps = 0;
double residual = 0;
HIPSOLVER_CHECK(hipsolverXsyevjGetSweeps(hipsolver_handle, params, &sweeps));
HIPSOLVER_CHECK(hipsolverXsyevjGetResidual(hipsolver_handle, params, &residual));
std::cout << "\nWhich was computed in " << sweeps << " sweeps, with a residual of " << residual
<< std::endl;
// 11. Validate that 'AV == VD' and that 'AV - VD == 0'.
std::cout << "\nLet D be the diagonal constructed from W.\n"
<< "The right multiplication of A * V should result in V * D [AV == VD]:"
<< std::endl;
// Right multiplication of the input matrix with the eigenvectors.
std::vector<double> AV(n * lda);
multiply_matrices(1.0, 0.0, n, n, n, A.data(), lda, 1, V.data(), 1, lda, AV.data(), lda);
#if PR_D
std::cout << "AV = " << format_range(AV.begin(), AV.end()) << std::endl;
#endif
// Construct the diagonal D from eigenvalues W.
std::vector<double> D(n * n);
for(int i = 0; i < n; i++)
{
D[(n + 1) * i] = W[i];
}
// Scale eigenvectors V with W by multiplying V with D.
std::vector<double> VD(n * lda);
multiply_matrices(1.0, 0.0, n, n, n, V.data(), 1, lda, D.data(), lda, 1, VD.data(), lda);
#if PR_D
std::cout << "VD = " << format_range(VD.begin(), VD.end()) << std::endl;
#endif
double epsilon = 1.0e5 * std::numeric_limits<double>::epsilon();
int errors = 0;
double mse = 0;
for(int i = 0; i < n * n; i++)
{
double diff = (AV[i] - VD[i]);
diff *= diff;
mse += diff;
errors += (diff > epsilon);
}
mse /= n * n;
std::cout << "\nMean Square Error of [AV == VD]:\n " << mse << std::endl;
// 12. Clean up device allocations.
HIPSOLVER_CHECK(hipsolverDestroy(hipsolver_handle));
HIPSOLVER_CHECK(hipsolverDestroySyevjInfo(params));
HIP_CHECK(hipFree(d_A));
HIP_CHECK(hipFree(d_W));
HIP_CHECK(hipFree(d_work));
HIP_CHECK(hipFree(d_info));
return report_validation_result(errors);
}
第一种 Makefile:
使用g++ 编译
SRC := hipsolver_Dsyevj.cpp
EXE := hipsolver_Dsyevj
all: $(EXE)
INC := -I/opt/rocm/include
LD_FLAGS := -L/opt/rocm/lib -lamdhip64 -lrocblas -lhipsolver -lrocsolver -D__HIP_PLATFORM_AMD__
%: %.cpp
g++ $< -o $@ $(INC) $(LD_FLAGS)
.PHONY: clean
clean:
rm -rf $(EXE)第二种 Makefile:
使用hipcc编译
EXAMPLE := hipsolver_syevj
COMMON_INCLUDE_DIR := ./Common
GPU_RUNTIME := HIP
# HIP variables
ROCM_INSTALL_DIR := /opt/rocm
CUDA_INSTALL_DIR := /usr/local/cuda
HIP_INCLUDE_DIR := $(ROCM_INSTALL_DIR)/include
HIPSOLVER_INCLUDE_DIR := $(HIP_INCLUDE_DIR)
HIPCXX ?= $(ROCM_INSTALL_DIR)/bin/hipcc
CUDACXX ?= $(CUDA_INSTALL_DIR)/bin/nvcc
# Common variables and flags
CXX_STD := c++17
ICXXFLAGS := -std=$(CXX_STD)
ICPPFLAGS := -isystem $(HIPSOLVER_INCLUDE_DIR) -I $(COMMON_INCLUDE_DIR)
ILDFLAGS := -L $(ROCM_INSTALL_DIR)/lib
ILDLIBS := -lhipsolver
ifeq ($(GPU_RUNTIME), CUDA)
CXXFLAGS += -x cu
CPPFLAGS += -D__HIP_PLATFORM_NVIDIA__
COMPILER := $(CUDACXX)
else ifeq ($(GPU_RUNTIME), HIP)
CXXFLAGS ?= -Wall -Wextra
CPPFLAGS += -D__HIP_PLATFORM_AMD__
COMPILER := $(HIPCXX)
else
$(error GPU_RUNTIME is set to "$(GPU_RUNTIME)". GPU_RUNTIME must be either CUDA or HIP)
endif
ICXXFLAGS += $(CXXFLAGS)
ICPPFLAGS += $(CPPFLAGS)
ILDFLAGS += $(LDFLAGS)
ILDLIBS += $(LDLIBS)
$(EXAMPLE): hipsolver_Dsyevj.cpp
$(COMPILER) -g $(ICXXFLAGS) $(ICPPFLAGS) $(ILDFLAGS) -o $@ $< $(ILDLIBS)
clean:
$(RM) $(EXAMPLE)
.PHONY: clean
3,编译运行
make
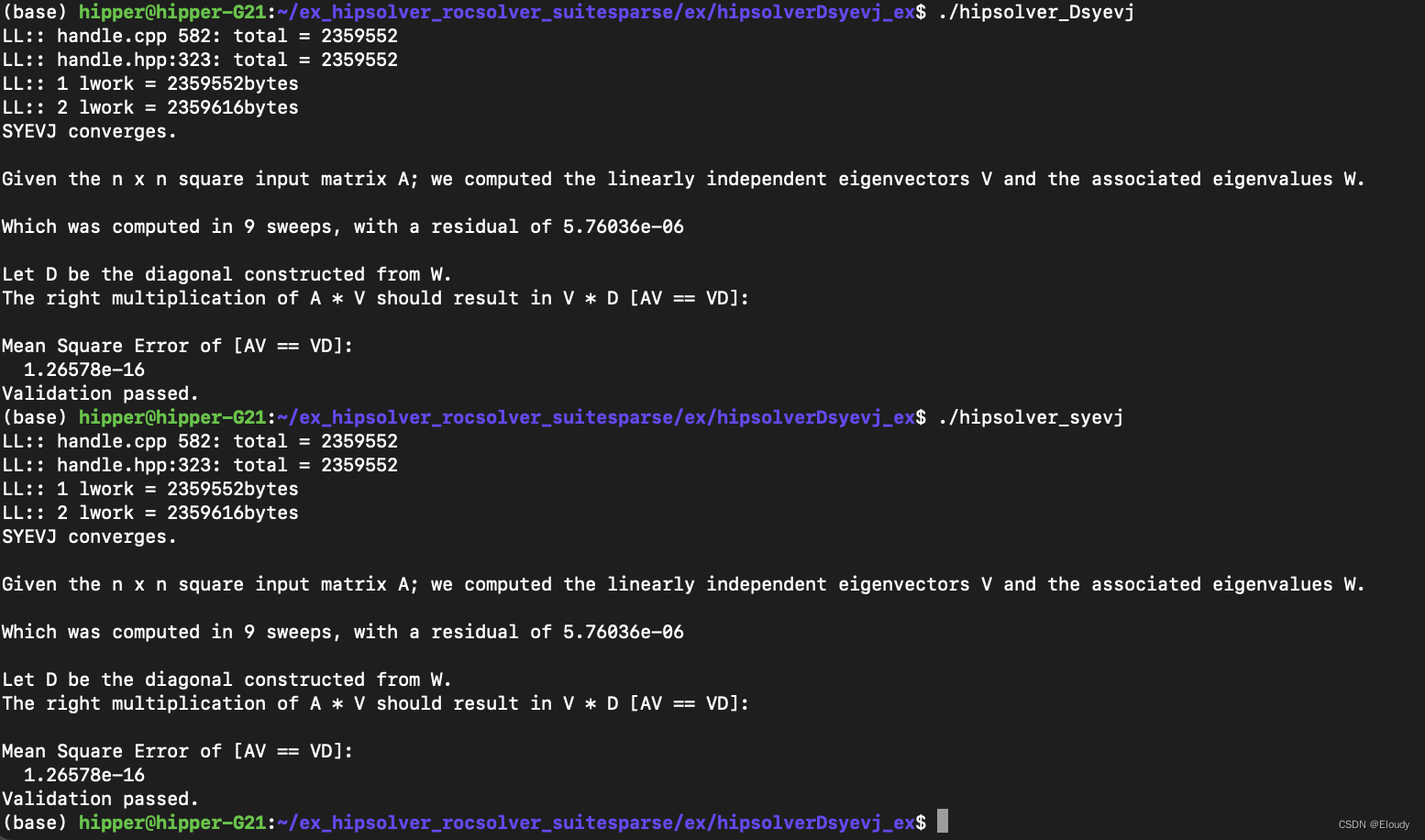
4,提炼出来了
git@github.com:Kleenelan/yevj_batched_little_rocm.git
5, 参考
GitHub - amd/rocm-examples
结束