1. 引言
扩散模型在近年来成为了热门话题,其火速蹿红主要归功于在图像生成领域的突破应用。尤其是一些从文本到图像的生成技术,它们成功地运用了扩散模型来创建令人惊叹的逼真图像。如果你听说过某个应用能够迅速且高质量地生成图像,那么很可能是以下几个知名项目之一:
- OpenAI推出的DALL·E,这是一个引领潮流的图像生成系统,以其独特的创造力和高质量输出著称。
- Google的Imagen,一个同样基于扩散模型的强大工具,它以生成高分辨率、极具细节的图像而闻名。
- Stable Diffusion,这是另一个在该领域取得显著成就的例子,它同样展现了扩散模型在图像生成中的强大潜力。
这些应用的成功不仅证明了扩散模型在处理复杂图像任务方面的有效性,还开启了图像生成技术的新纪元,为未来的创新奠定了基础。随着技术的进步,我们可以预见扩散模型将在视觉艺术、设计、娱乐等领域发挥更大的影响。

扩散模型的概念和重要性
在自然科学和工程学中,Diffusion扩散模型是研究物质、能量、信息等如何在空间中传播的重要工具。扩散是指某种实体在空间中由高浓度区域向低浓度区域移动的过程,这种现象在自然界中无处不在,从气体分子的运动到森林火灾的蔓延,都可以用扩散模型来描述。这种模型的研究不仅对理解自然现象至关重要,也在工业、社会学、生物学等多个领域有着广泛的应用。
Diffusion模型在不同领域的应用简介
扩散模型的应用范围极为广泛,其在不同学科领域中的应用各有侧重。在物理学中,扩散模型被用来研究热传导、粒子扩散等现象。在生物学中,它帮助科学家们理解细胞内物质的传输机制。在化学领域,扩散模型对于分析化学反应和物质混合过程至关重要。
此外,扩散模型在社会科学领域也发挥着重要作用。例如,在研究社会网络和人口迁移时,扩散模型可以用来模拟信息、趋势或行为模式的传播过程。在环境科学中,扩散模型用于研究污染物在环境中的扩散和分布。在经济学领域,扩散理论可以用来分析创新或新技术的市场渗透。
这些应用示例表明,Diffusion扩散模型不仅是一个理论工具,更是一个跨学科领域的桥梁,它帮助我们从宏观角度理解复杂现象的传播和演变过程。
综上所述,Diffusion扩散模型因其在多个学科中的广泛应用而显得尤为重要。它不仅加深了我们对物理世界的理解,也为处理实际问题提供了有效的方法。
2. Diffusion模型的理论基础
扩散过程的研究起源于物理学,旨在解释物质如何通过随机运动在空间中均匀分布的现象。这一部分将探讨扩散的物理和数学原理,以及不同类型的扩散模型。
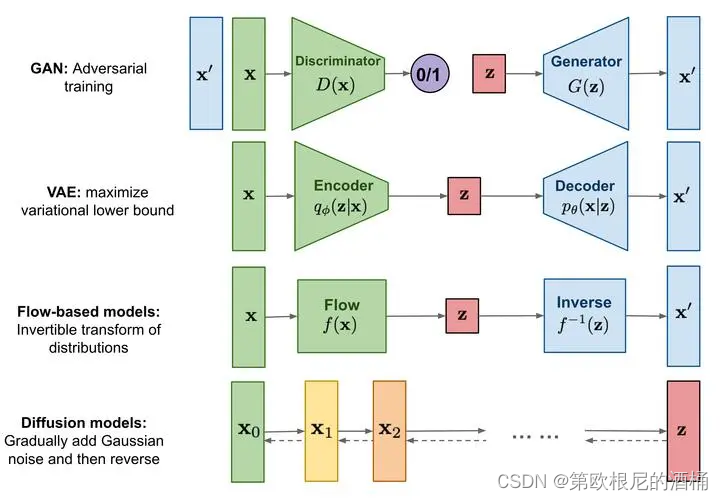
扩散过程的物理和数学原理
扩散过程可以被视为大量微观粒子的随机运动的宏观结果。这些粒子由于动力学效应而从高浓度区域向低浓度区域移动。在数学上,这一过程通常由Fick的第一定律来描述,其表达式为:
J = − D ∇ ϕ J = -D \nabla \phi J=−D∇ϕ
这里, J J J 表示扩散通量(即单位时间内穿过单位面积的物质的数量), D D D 是扩散系数, ∇ ϕ \nabla \phi ∇ϕ 是浓度梯度。Fick的第一定律表明,扩散通量与浓度梯度成反比,且方向相反。
不同类型的扩散模型
-
Fick扩散:这是最常见的扩散模型类型,适用于许多简单系统。它假设扩散系数是常数,这意味着物质的扩散速率不随时间和位置变化。
-
随机游走扩散:在这种模型中,粒子的运动被视为一系列随机步骤的结果。这种模型对于理解扩散在不规则或复杂介质中的行为特别有用。
扩散方程的基本形式及其推导
扩散过程也可以用偏微分方程来描述,这通常称为Fick的第二定律。它描述了浓度随时间和空间变化的方式:
∂ ϕ ∂ t = D ∇ 2 ϕ \frac{\partial \phi}{\partial t} = D \nabla^2 \phi ∂t∂ϕ=D∇2ϕ
这里, ∂ ϕ ∂ t \frac{\partial \phi}{\partial t} ∂t∂ϕ 表示浓度随时间的变化率, ∇ 2 \nabla^2 ∇2 是Laplacian算子,代表浓度的空间变化。这个方程说明,一个区域内的物质浓度变化率是由其浓度的空间分布决定的。
扩散系数的定义和意义
扩散系数 D D D是描述物质在特定介质中扩散速率的参数。它取决于多种因素,如温度、介质的性质和粒子的大小。在实际应用中,确定合适的扩散系数对于模型的准确性至关重要。
边界条件和初始条件在扩散模型中的作用
解决扩散方程还需要考虑边界条件和初始条件。边界条件描述了系统边界上的物质行为,如绝对隔绝或恒定浓度。初始条件则指定了开始时刻系统的状态。这些条件对于模型的解具有决定性影响。
3. Diffusion模型的数学描述
为了深入理解Diffusion扩散模型,我们需要探讨其数学描述,包括扩散方程的推导、关键参数的意义,以及模型的求解过程。
扩散方程的推导
Diffusion过程通常用偏微分方程来描述,这是从Fick的第一定律和守恒定律推导出的。Fick的第二定律提供了一个方程,描述了随时间变化的物质浓度分布:
∂ ϕ ∂ t = D ∇ 2 ϕ \frac{\partial \phi}{\partial t} = D \nabla^2 \phi ∂t∂ϕ=D∇2ϕ
在这个方程中, ϕ \phi ϕ 表示浓度, ∂ ϕ ∂ t \frac{\partial \phi}{\partial t} ∂t∂ϕ 是浓度随时间的变化, D D D 是扩散系数,而 ∇ 2 ϕ \nabla^2 \phi ∇2ϕ(Laplacian of ϕ \phi ϕ)描述了空间中的浓度变化。
扩散系数的意义
扩散系数 D D D是一个关键参数,它影响物质扩散的速率。不同物质和不同介质的 D D D值可能有很大差异。例如,气体中的扩散系数通常比液体中的大得多。
边界条件和初始条件
在解决扩散方程时,边界条件和初始条件对于确定唯一解至关重要。边界条件定义了系统的物理边界,如隔绝边界或恒定浓度边界。初始条件则指出了扩散开始时浓度的分布。
求解扩散方程
扩散方程的求解可以通过分析方法(对于简单情形)或数值方法(对于复杂情况)。分析解提供了方程的精确解,而数值方法(如有限差分法)则适用于更复杂的系统。
扩散模型求解的流程图
以上流程图展示了求解Diffusion扩散模型的一般步骤,包括定义问题、设置初始和边界条件、确定扩散系数、建立方程,以及求解和分析结果。
4. 扩散模型的应用实例
Diffusion扩散模型由于其广泛的应用,成为了许多科学领域研究的基石。以下是一些具体的应用实例。
在自然科学领域的应用
-
物理学中的热传导:扩散模型用于描述热量如何通过物质传播。这在研究绝缘材料或构建更有效的热交换器方面非常重要。
-
生物学中的物质传递:在细胞生物学中,扩散模型用来描述如何通过细胞膜进行物质交换,这对于理解细胞内外物质如何传递至关重要。
-
化学反应中的分子扩散:扩散模型帮助化学家理解和预测在化学反应中分子如何移动和互相作用。
在社会科学领域的应用
-
人口迁移:在社会学和人口统计学中,扩散模型被用来模拟和分析人群在不同地区之间的迁移模式。
-
信息传播:在传播学和社交网络分析中,扩散模型用于研究信息、新闻或趋势如何在社交网络中扩散。
在工业和工程领域的应用
-
材料科学:在材料科学中,扩散模型用于研究和优化材料的热处理过程,以及研究合金中不同元素的分布。
-
环境工程:扩散模型在环境工程中用于模拟污染物在水体或大气中的扩散过程,对于污染控制和环境保护至关重要。
代码演示:使用公开数据集进行扩散模拟
接下来,我们将通过一个Python代码示例展示如何使用公开数据集来模拟一个简单的扩散过程。假设我们要模拟某种污染物在水体中的扩散。
首先,我们需要准备数据。这里我们使用一个模拟的数据集,代表了污染物在不同时间点的浓度分布。数据可以是一个二维数组,其中每个元素代表污染物在特定位置的浓度。
import numpy as np
import matplotlib.pyplot as plt
# 创建一个模拟的污染物浓度分布数据
initial_concentration = np.zeros((100, 100))
initial_concentration[50:55, 50:55] = 100 # 在中心区域设置高浓度
# 展示初始浓度分布
plt.imshow(initial_concentration, cmap='hot', interpolation='nearest')
plt.show()
此代码段创建了一个100x100的网格,其中中心有一个高浓度的区域,模拟了污染物的初始分布情况。接下来,我们将实现扩散过程的数值模拟。
对于扩散过程的数值模拟,我们可以使用离散时间步长和有限差分法来近似地解决扩散方程。以下是扩散模拟的实现:
def diffuse(concentration, diffusion_coefficient, dt, dx):
"""
执行一次扩散迭代。
:param concentration: 当前的浓度分布。
:param diffusion_coefficient: 扩散系数。
:param dt: 时间步长。
:param dx: 空间步长。
:return: 更新后的浓度分布。
"""
# 计算扩散项
laplacian = np.roll(concentration, 1, axis=0) + np.roll(concentration, -1, axis=0) \
+ np.roll(concentration, 1, axis=1) + np.roll(concentration, -1, axis=1) \
- 4 * concentration
# 更新浓度
concentration += diffusion_coefficient * laplacian * dt / (dx ** 2)
return concentration
# 扩散系数、时间步长和空间步长
D = 0.1
dt = 0.1
dx = 1
# 执行多次扩散迭代
for t in range(100):
initial_concentration = diffuse(initial_concentration, D, dt, dx)
# 每隔一定时间步长展示浓度分布图
if t % 10 == 0:
plt.imshow(initial_concentration, cmap='hot', interpolation='nearest')
plt.title(f"Time step: {t}")
plt.show()
这个代码示例展示了如何模拟扩散过程。我们定义了一个diffuse函数,它根据扩散系数和离散时间、空间步长更新浓度分布。通过多次迭代,可以观察到污染物浓度随时间在空间中的扩散。
与其他模型的比较
在实际应用中,扩散模型通常与其他类型的模型结合使用,以更准确地描述复杂系统。例如,在生态系统模型中,扩散过程可能与生物增长模型结合,以模拟物种的扩散和种群动态。
5. Diffusion模型的挑战和未来发展
尽管Diffusion扩散模型在多个领域中得到了成功应用,但仍存在一些挑战,这些挑战激发了新的研究方向和发展。
当前扩散模型面临的主要挑战
-
非线性和异质性:现实世界中的许多扩散过程并非简单的线性过程。例如,扩散系数 D D D可能随浓度或位置而变化,导致扩散过程变得更加复杂。
∂ ϕ ∂ t = ∇ ⋅ ( D ( ϕ , x ) ∇ ϕ ) \frac{\partial \phi}{\partial t} = \nabla \cdot (D(\phi, \mathbf{x}) \nabla \phi) ∂t∂ϕ=∇⋅(D(ϕ,x)∇ϕ)
这里, D ( ϕ , x ) D(\phi, \mathbf{x}) D(ϕ,x)表示扩散系数可以是浓度 ϕ \phi ϕ和位置 x \mathbf{x} x的函数,这使得方程变为非线性的。
-
多物理场的耦合:在许多情况下,扩散过程与其他物理过程如流体动力学、热传导或化学反应相互作用。这些耦合效应的考虑对于理解复杂系统中的扩散至关重要。
未来发展趋势和潜在研究领域
-
扩散模型的多尺度模拟:发展能够同时考虑微观和宏观尺度扩散过程的模型,可以帮助我们更全面地理解复杂系统中的扩散现象。
-
结合机器学习和数据科学:利用机器学习算法来预测和分析扩散过程,尤其是在数据丰富但理论模型不足的领域,例如生物医药和材料科学。
-
环境和社会系统中的应用:扩散模型在环境科学和社会科学中的应用日益增多,特别是在气候变化、疾病传播和社会行为动态方面。
参考文献和资源
- 非线性扩散过程的数学理论
- 多物理场耦合模型的开发和应用
- 机器学习在扩散模型中的应用案例研究
6. 结论
Diffusion扩散模型作为理解和描述物质、能量、信息等在空间中传播的关键工具,在科学研究和工程应用中占据了重要地位。本文综合介绍了扩散模型的基本原理、数学描述、应用实例以及面临的挑战和未来发展。
Diffusion扩散模型的重要性和影响
扩散模型不仅提供了一种分析和预测物理世界现象的方法,而且在社会科学、生态学和许多其他领域中也展现出了广泛的应用潜力。从物理学中的热传导到社会学中的信息传播,扩散模型帮助我们理解了这些过程的基本规律。
对未来扩散模型研究的展望
随着计算能力的增强和数据科学的发展,扩散模型的应用和研究正变得越来越精细和复杂。未来的研究可能会集中在以下几个方向:
-
多尺度和多物理场扩散模型的开发:结合不同尺度和物理过程的扩散模型,以更全面地描述复杂系统中的扩散行为。
-
机器学习和人工智能在扩散模型中的应用:利用先进的数据分析技术来提高扩散模型的预测能力和应用范围。
-
解决全球性挑战:在气候变化、疾病控制和环境保护等领域,运用扩散模型来解决全球性挑战。
参考文献和资源
为了进一步探索扩散模型的各个方面,以下是一些有用的参考资源:
- 扩散过程的多尺度建模
- 机器学习在扩散模型中的应用
- 扩散模型在环境科学中的应用
综上所述,Diffusion扩散模型在多个学科领域内都展现了其独特的价值和潜力。随着技术的发展和研究的深入,这些模型将继续在解决复杂问题和推动科学进步方面发挥重要作用。
7. 结论
随着科学和工程领域的快速发展,Diffusion扩散模型在揭示和解释各种自然现象、社会现象以及工程问题中扮演了至关重要的角色。本文全面探讨了扩散模型的理论基础、应用实例、挑战以及未来的发展前景。
Diffusion扩散模型在自然科学中的重要性
在物理、化学和生物学等自然科学领域,扩散模型提供了一个基本框架,用以理解物质和能量在空间中的传播机制。从分子水平的物质交换到大规模的气候变化过程,扩散模型都是不可或缺的分析工具。这些模型不仅帮助科学家们解释已知现象,还预测了许多新的科学问题。
Diffusion扩散模型在工程和技术中的应用
在工程领域,扩散模型对于优化设计和改善工艺流程具有重要意义。在材料科学、环境工程和化学工程等领域,通过扩散模型的应用,我们可以设计出更有效的材料,更好地控制污染物的传播,以及优化化学反应过程。这些应用对于提高工业效率和促进可持续发展具有深远的影响。
扩散模型在社会科学中的角色
社会科学中的扩散模型帮助我们理解信息、文化、创新和行为模式是如何在社群中传播的。这些模型在市场研究、流行病学、社交网络分析等领域提供了宝贵的洞见,帮助我们理解和预测社会动态。
未来展望:跨学科的合作和创新
展望未来,Diffusion扩散模型的研究将继续与其他学科领域的研究相结合,尤其是在数据科学和人工智能方面的合作将为扩散模型带来新的发展机遇。通过利用大数据和机器学习技术,我们可以更精确地模拟复杂系统中的扩散过程,从而在理解复杂现象和解决实际问题方面取得更大的进步。
总而言之,Diffusion扩散模型作为一个跨学科的研究工具,不仅在理论上增进了我们对世界的理解,也在实践中带来了实际应用的革新。随着科技的不断进步,我们可以期待这些模型在未来将会有更广泛的应用,为人类社会的发展做出更大的贡献。