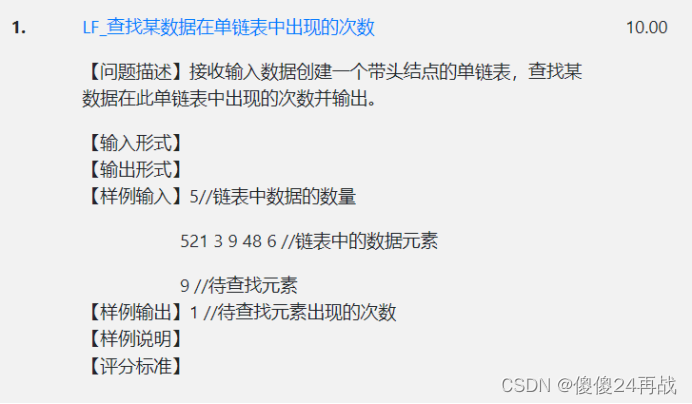
一句话总结：不是太难，状态转移方程好想。

原题链接：62 不同路径

位置为(i, j)的点只能从上面或者左边过来，由此可列出状态转移方程。状态转移方程的初始化为所有第一排和第一列的点都初始化为1即可。

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; ++i) dp[i][0] = 1;
        for (int i = 1; i < n; ++i) dp[0][i] = 1;
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

 原题链接：63 不同路径II

与上一题类似，只是增加了障碍物条件，那么只需要在(i, j)点为1时将dp[i, j]设置为0即可。同时dp数组初始化时也是在(i, j)点为1时，该点及之后各点dp值均保持为0即可。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length, n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; ++i) {
            if (obstacleGrid[i][0] == 0) dp[i][0] = 1;
            else break;
        } 
        for (int i = 0; i < n; ++i) {
            if (obstacleGrid[0][i] == 0) dp[0][i] = 1;
            else break;
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (obstacleGrid[i][j] == 0) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}