今日任务:
1)77.组合
77.组合
题目链接:77. 组合 - 力扣(LeetCode)
文章讲解:代码随想录 (programmercarl.com)
视频讲解:带你学透回溯算法-组合问题(对应力扣题目:77.组合)| 回溯法精讲!哔哩哔哩bilibili
带你学透回溯算法-组合问题的剪枝操作(对应力扣题目:77.组合)| 回溯法精讲!哔哩哔哩bilibili
思路:
直截了当就是暴力法,循环遍历就行,但是当k比较大时,这不好写了,相当于循环嵌套50层。这个时候可以采用递归(回溯),传入遍历起始和终止点
注意:哪怕采用回溯,也是穷举法,只是写起来方便
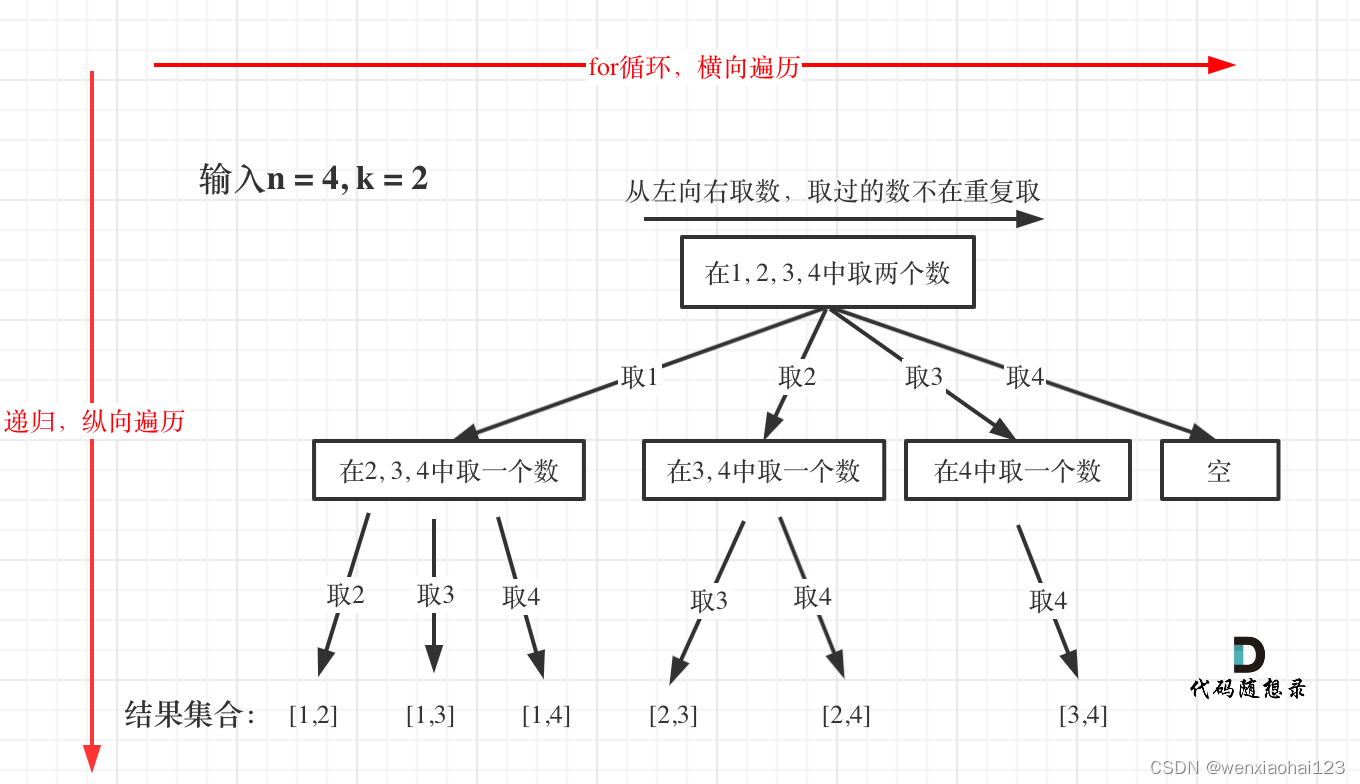
举例:
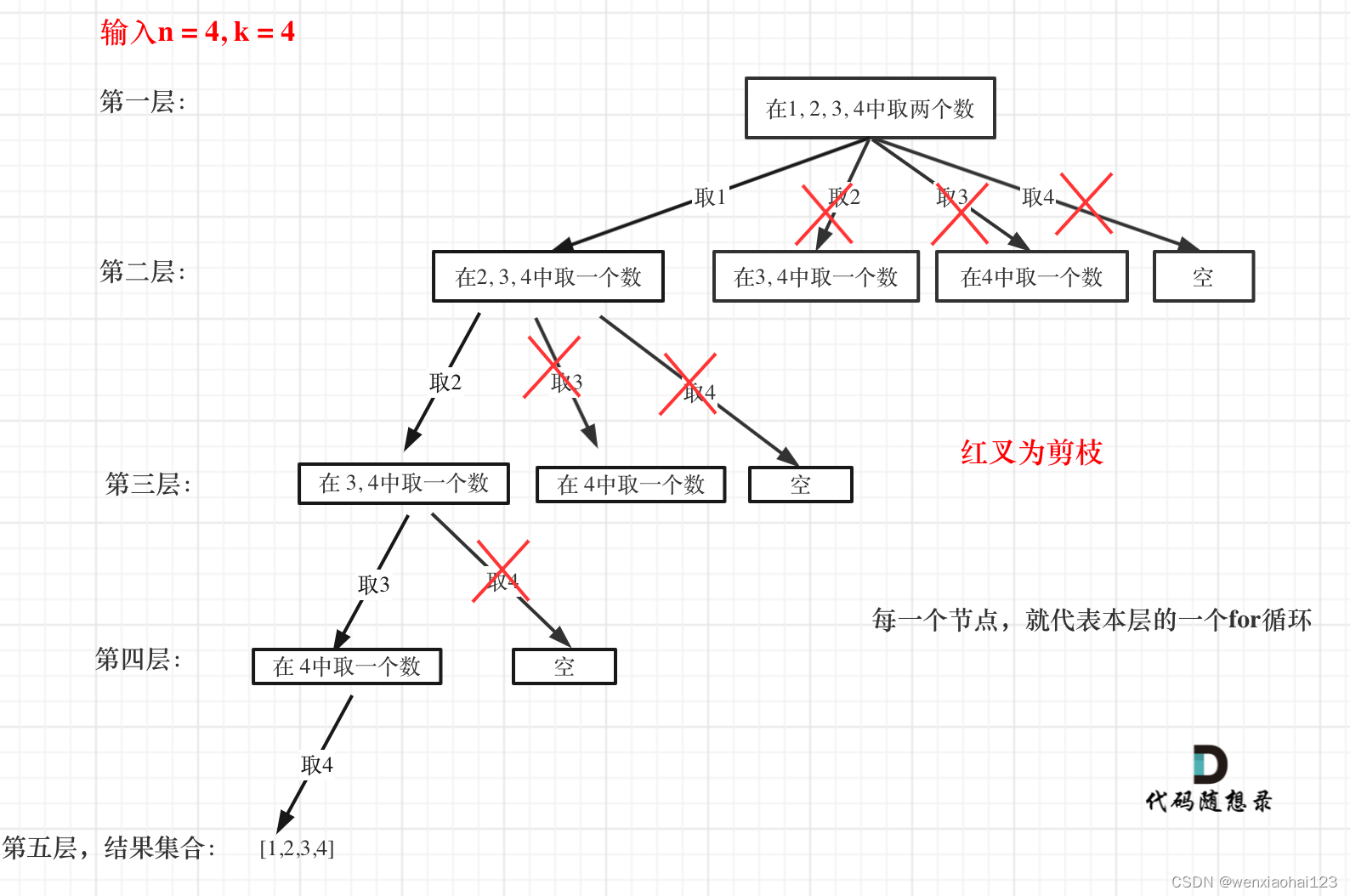
第一层循环遍历到1,存入数组中,接着第二层遍历从2开始遍历,得到[1,2],满足要求,可以返回,回到第二层的遍历,到3,此时数组中已经有[1,2],了所以在返回第二层遍历前,我们还需要回溯,弹出2,再回到第二层遍历,此时添加3,得到[1,3],弹出3····
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = []
self.traveral(n, k, 1, [], result)
return result
def traveral(self, n, k, start, path, result):
# 递归层
for i in range(start, n + 1):
path.append(i)
# 终止条件
if len(path) == k:
result.append(path[:])
else:
self.traveral(n, k, i + 1, path, result)
path.pop()这种方法会遍历所有的情况,我们可以对上面代码进行一些优化
-
提前剪枝: 当当前路径的长度已经达到了目标长度
k时,就不需要再继续递归了,可以直接返回,避免不必要的递归调用。 -
优化递归函数的参数传递: 可以将
result参数设置为类的成员变量,这样在递归调用中就不需要传递该参数了。 -
补充剪枝:当剩下的可选数不够了,直接剪枝
举个例子:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
# 将result变为成员变量,省略传递
self.result = []
self.traversal(n, k, 1, [])
return self.result
def traversal(self, n: int, k: int, start: int, path: List[int]) -> None:
# 终止条件:当前路径长度等于 k
if len(path) == k:
self.result.append(path[:])
return
# 递归层
for i in range(start, n + 1):
# 提前剪枝:如果剩余可选数的个数不够,直接返回
if n - i + 1 < k - len(path):
return
path.append(i)
self.traversal(n, k, i + 1, path)
path.pop()感想:这题不算难,但是需要自己画图想清楚,还不是很清晰的时候,可以先写一点,打印中间过程,对递归就比较清晰了