62.不同路径

题目链接

https://leetcode.cn/problems/unique-paths/description/

题目描述

思路

dp[i][j] 表示的是走到（i，j）有多少种不同的路径
第一行和第一列都需要初始化为1，因为这些位置都只有一种路径

class Solution {
    public int uniquePaths(int m, int n) {
        //1、定义 dp 数组
        //dp[i][j]:表示到达（i，j）点有多少条路径
        int[][] dp = new int[m][n];
        //初始化第一行和第一列
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n; j++) {
            dp[0][j] = 1;
        }
        //遍历数组
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

63. 不同路径 II

题目链接

https://leetcode.cn/problems/unique-paths-ii/description/

题目描述

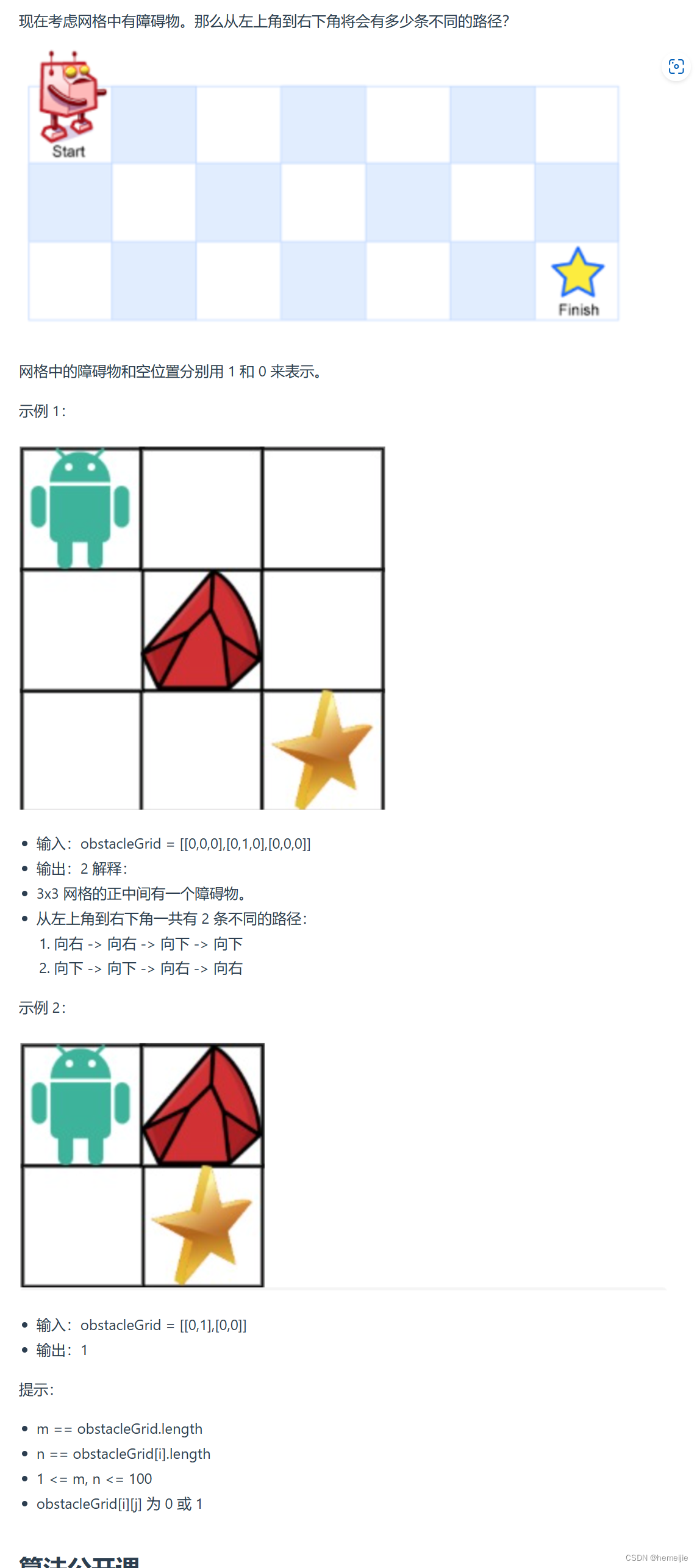
思路

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        //获取数组的行和列
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        if(obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1){
            return 0;
        }
        //建立 dp 数组
        int[][] dp = new int[m][n];
        //初始化第一列，同时第一列中不能有障碍物
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
            dp[i][0] = 1;
        }
        //初始化第一行，并且第一行中不能有障碍物
        for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) {
            dp[0][i] = 1;
        }
        //遍历数组
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                //不能有障碍物
                if(obstacleGrid[i][j] == 0){
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }