图的基本概念


图的种类

怎么存放图呢?
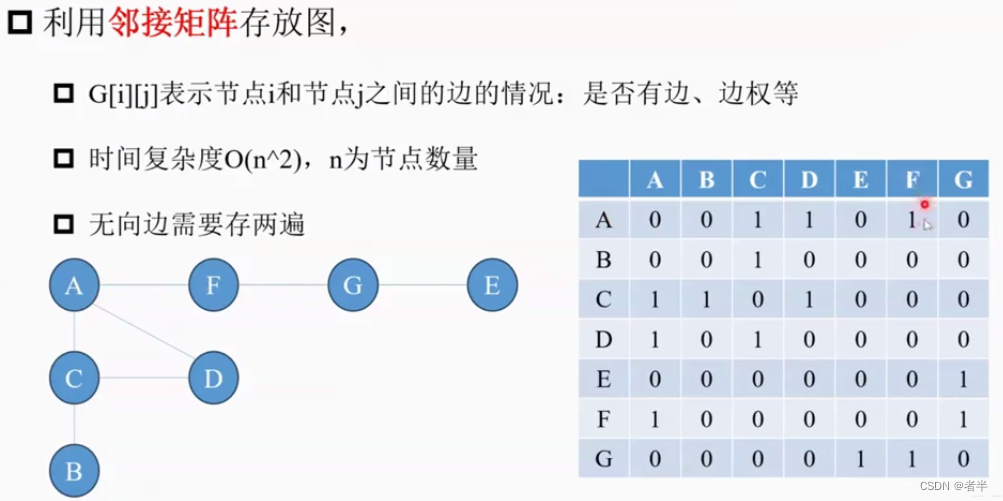
优化
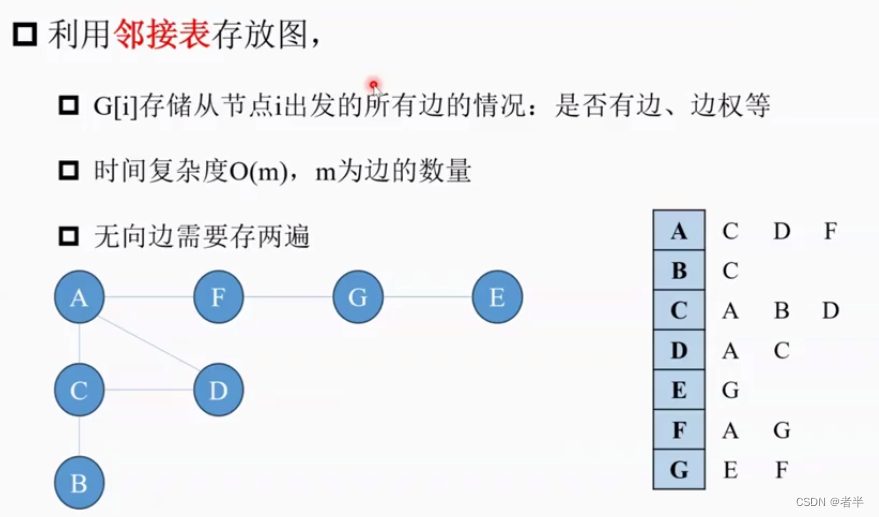
DFS
不是最快/最好的路,但是能找到一条连通的道路。(判断两点之间是不是连通的)
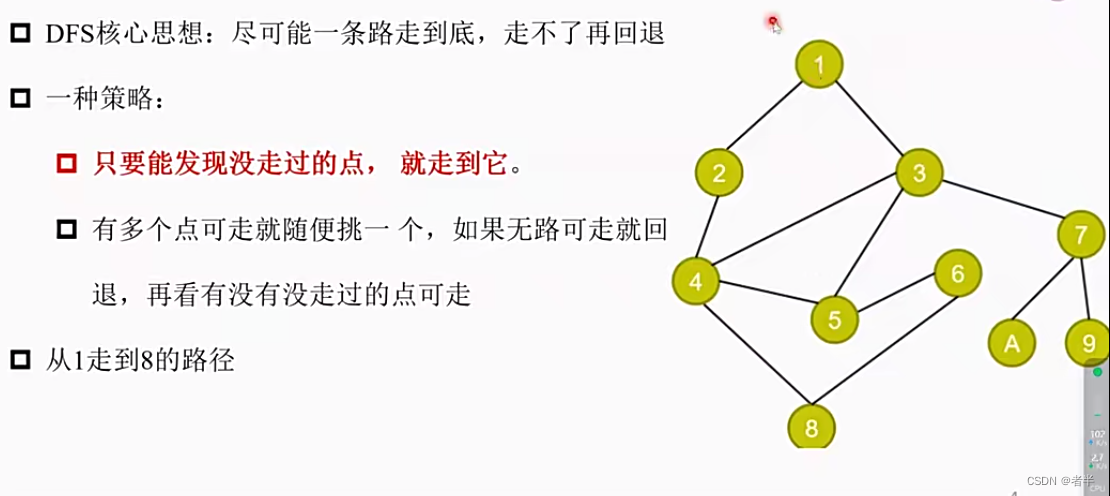

蓝桥3891


import os
import sys
sys.setrecursionlimit(100000)
# 请在此输入您的代码
n, m = map(int, input().split()) # n个点, 小明序号m
G = [[] for _ in range(n + 1)] # 邻接表,存放图。
rudu = [0] * (n + 1) # 记录每个点的入度
vis = [0] * (n + 1) # dfs的标记数组,看是否遍历过
# 二元组,分别表示每个子树数量和编号
dis = [[0, i] for i in range(n + 1)] # 排序用的二元组
for _ in range(n - 1):
l, r = map(int, input().split())
G[r].append(l) # r是l的父亲
rudu[l] += 1
for i in range(1, n + 1):
if rudu[i] == 0:
root = i # 入度为0的是根节点,找到根节点,从根节点开始遍历。
def dfs(u):
# 同时记录每个点的子树节点数
dis[u][0] = -1 # 1改成-1,以便都从小到大排序
vis[u] = 1
for v in G[u]:
if vis[v] == 0:
dfs(v)
dis[u][0] += dis[v][0]
dfs(root)
dis.sort()
# print(dis)
for i, (x, y) in enumerate(dis, 1): # 取出dis的排名,1的意思是索引从1开始
if y == m:
print(i)
breakBFS

按层次分节点(几步能走的点)

不断这样取,直到终点。
蓝桥1509


import os
import sys
# 请在此输入您的代码
from collections import deque
def bfs(s, t):
# s起点, t终点。
dis = [-1] * 100001
queue = deque()
# 将起点塞入队列中,打上标记。
queue.append(s)
dis[s] = 0
# 当队列非空
while len(queue) != 0:
# 取出队首元素u
u = queue.popleft()
# 判断u是否为终点
if u == t:
return dis[u]
# 将u相连的所有点v,只要v未标记,则打标记,入队列
for v in [u - 1, u + 1, u * 2]:
# 特判:越界、已标记、障碍物
if 0 <= v <= 100000 and dis[v] == -1:
queue.append(v)
dis[v] = dis[u] + 1
return -1
n, k = map(int, input().split())
print(bfs(n, k))蓝桥3819



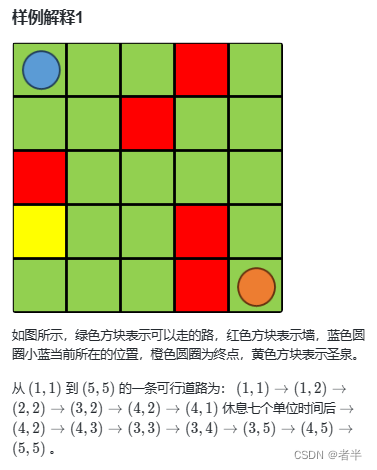
import os
import sys
# 请在此输入您的代码
from collections import deque
def bfs(x, y, dis):
queue = deque()
vis = [[0] * m for i in range(n)]
# 将起点入队列
queue.append([x, y])
dis[x][y] = 0
vis[x][y] = 1
while len(queue) != 0:
x, y = queue.popleft()
# 要求所有点,这步省略
for deltax, deltay in [(1, 0), (0, 1), (-1, 0), (0, -1)]:
xx, yy = x + deltax, y + deltay
# 未越界,未标记,未障碍物
if 0 <= xx < n and 0 < yy < m and vis[xx][yy] == 0 and g[xx][yy] != '#':
queue.append([xx, yy])
dis[xx][yy] = dis[x][y] + 1
vis[xx][yy] = 1
n, m = map(int, input().split())
INF = 1e9 # 把路堵死了,永远走不到终点。
A, B, C, D = map(int, input().split())
A, B, C, D = A - 1, B - 1, C - 1, D - 1
g = [input() for i in range(n)]
E = int(input())
dis1 = [[INF] * m for i in range(n)]
dis2 = [[INF] * m for i in range(n)]
bfs(A, B, dis1)
bfs(C, D, dis2)
res = dis1[C][D]
if res <= E:
print(res)
else:
# 枚举所有圣泉
res = INF
for i in range(n):
for j in range(m):
if g[i][j] == 'V':
res = min(res, dis1[i][j] + dis2[i][j])
if res == INF:
print("No")
else:
# 初始能量为E,总距离res, 后面的res-E需要花费两倍时间,因为需要等待能量恢复
print((res - E) * 2 + E)拓扑排序
拓扑排序是一种针对“有向无环图”的算法,用于解决一些有依赖关系的问题。
拓扑排序保证了处理到某个点时,其所有的入点已经处理过了。
例如下面这个图,拓扑排序可以保证:
处理点2之前,点4和点6都处理过。
处理点3之前,点2和点6都处理过。
比如学大学物理必须先学高数和线性代数。
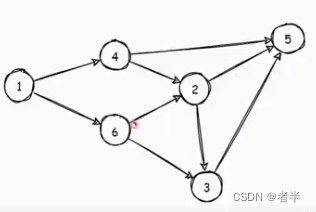
拓扑排序的顺序并不是唯一的,就刚刚的例子,你可以先学高数再学线代,也可以先学线代再学高数。
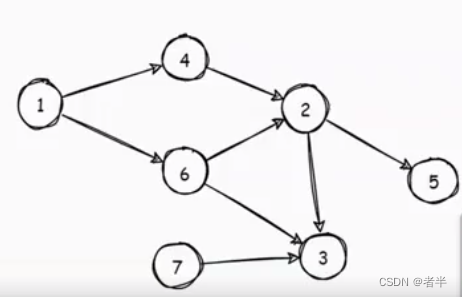
下图是拓扑排序的几种可能性
如果有环的话找不到起点,自己想想应该就能想出来。
BFS实现拓扑排序
- 先预处理每个点的入度,这个在读入边的时候处理。
- 每次将入度为0的点入队列。
- 每次取点u的时候,对于从u出发的所有点v的入度-1
1此时的入度为0,相当于做了一个操作,把1->4和1->6的边给删掉了,然后发现4和6的入度又为0了。
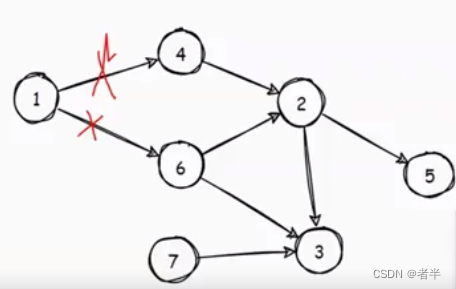
- 在枚举边u->v的时候,可以进行状态转移,于是可以和动态规划结合起来。
- 这样的dp也叫DAG-DP(有向无环图上的动态规划)
- 状态转移一般只发生在枚举所有边的时候。
模板
from collections import deque
def topo():
q = deque()
for i in range(1, n + 1):
if ru[i] == 0:
q.append(i)
ans = []
while len(q) != 0:
u = q.popleft()
ans.append(u)
for v in G[u]:
ru[v] -= 1
if ru[v] == 0:
q.append(v)
if len(ans) != n:
print("no topo")
else:
print(*ans, sep=' ')n, m = map(int, input().split())
G = [[] for i in range(n + 1)]
ru = [0] * (n + 1)
for _ in range(m):
u, v = map(int, input().split())
G[u].append(v)
topo()蓝桥1337


import os
import sys
# 请在此输入您的代码
from collections import deque
def topo():
q = deque()
for i in range(1, n + 1):
if ru[i] == 0:
q.append(i)
while len(q) != 0:
# 取出队首元素
u = q.popleft()
# 对于和u相邻的每个点v
for v in G[u]:
# 从u走到v,说明dp[v]可以从dp[u] + 1转移过来
dp[v] = max(dp[v], dp[u] + 1)
ru[v] -= 1
if ru[v] == 0:
q.append(v)
# dp[i] 表示走到i的最长路,也就是最大值。
n, m = map(int, input().split())
dp = [0] * (n + 1)
G = [[] for i in range(n + 1)]
ru = [0] * (n + 1)
for _ in range(m):
u, v = map(int, input().split())
G[u].append(v)
topo()
print(max(dp))蓝桥3351


import os
import sys
from queue import PriorityQueue
# 请在此输入您的代码
def topo():
q = PriorityQueue()
for i in range(1, n + 1):
if ru[i] == 0:
q.put(i)
ans = []
while not q.empty():
u = q.get()
ans.append(u)
for v in G[u]:
ru[v] -= 1
if ru[v] == 0:
q.put(v)
if len(ans) != n:
print(-1)
else:
print(*ans, sep=' ')
n, m = map(int, input().split())
G = [[] for i in range(n + 1)]
ru = [0] * (n + 1)
for _ in range(m):
u, v = map(int, input().split())
G[u].append(v)
ru[v] += 1
topo()