线性回归
矩阵求导:
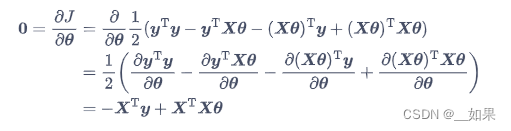
左边是分子布局,右边是分母布局,一般都用分母布局

解析解与数值解:
解析解是严格按照公式逻辑推导得到的,具有基本的函数形式。给出任意的自变量就可以求出其因变量
数值解是采用某种计算方法,在特定的条件下得到的一个近似数值结果,如有限元法,数值逼近法,插值法等等得到的解
对于方程x^2 = 2
其解析解为:±√2
其数值解为:±1.414213......
归一化:
# 数据归一化
scaler = StandardScaler()
scaler.fit(train) # 只使用训练集的数据计算均值和方差
train = scaler.transform(train)
test = scaler.transform(test)Q:为什么要归一化?
A:
,不同特征往往会有不同的量纲,归一化讲数据控制在0~1或-1~1,可以消除量纲的影响
RMSE与MSE:
我在时序预测的数据挖掘中第一次遇到RMSE,说是对异常值不那么敏感,然后可以对齐量纲,也就是从平方变回一次

训练:
# 在X矩阵最后添加一列1,代表常数项
X = np.concatenate([x_train, np.ones((len(x_train), 1))], axis=-1)
# @ 表示矩阵相乘,X.T表示矩阵X的转置,np.linalg.inv函数可以计算矩阵的逆
theta = np.linalg.inv(X.T @ X) @ X.T @ y_train
print('回归系数:', theta)
# 在测试集上使用回归系数进行预测
X_test = np.concatenate([x_test, np.ones((len(x_test), 1))], axis=-1)
y_pred = X_test @ theta
# 计算预测值和真实值之间的RMSE
rmse_loss = np.sqrt(np.square(y_test - y_pred).mean())
print('RMSE:', rmse_loss)x_train 和一个全为1的列向量(代表常数项)按列方向连接起来,形成一个新的增广矩阵 X。因为线性模型是y=θx,没有偏置(b),这里加一列1学一个偏置(b)
np.linalg.inv求逆矩阵,@矩阵内积
 线性回归模型使用最小二乘法求解正规方程,可以直接得到使得损失函数最小化的参数值
线性回归模型使用最小二乘法求解正规方程,可以直接得到使得损失函数最小化的参数值
print('回归系数:', linreg.coef_, linreg.intercept_)linreg.coef_ 是一个数组,包含了线性回归模型的系数,其中每个元素对应一个特征的系数
linreg.intercept_ 是一个标量,表示线性回归模型的常数项,即截距
梯度下降:
解析解中涉及大量的矩阵运算,非常耗费时间和空间
在更广泛的机器学习模型中,大多数情况下我们都无法得到解析解,或求解析解非常困难
![]() 梯度下降公式
梯度下降公式
 ∇θfθ(x) = x
∇θfθ(x) = x

像这个就是之前讲的到别的谷底去了
SGD:
梯度下降的公式已经不含有矩阵求逆和矩阵相乘等时间复杂度很高的运算,但当样本量很大时,计算矩阵与向量相乘仍然很耗时,矩阵的存储问题也没有解决。因此,我们可以每次只随机选一个样本计算其梯度,并进行梯度下降。
所以会歪歪扭扭的,因为不同样本点处的梯度不一定一样
MBGD:
Mini-Batch Gradient Descent(小批量梯度下降)
把样本分批次,例如100个样本分20批,一批就有5个样本,然后每次5个样本一起计算梯度,进行梯度下降
def batch_generator(x, y, batch_size, shuffle=True):
# 批量计数器
batch_count = 0
if shuffle:
# 随机生成0到len(x)-1的下标
idx = np.random.permutation(len(x))
x = x[idx]
y = y[idx]
while True:
start = batch_count * batch_size
end = min(start + batch_size, len(x))
if start >= end:
# 已经遍历一遍,结束生成
break
batch_count += 1
yield x[start: end], y[start: end]batch也就是批,batch size是一个批有几个样本,batch count是记录yield了几个,可以认为是return了几个batch出去
def SGD(num_epoch, learning_rate, batch_size):
# 拼接原始矩阵
X = np.concatenate([x_train, np.ones((len(x_train), 1))], axis=-1)
X_test = np.concatenate([x_test, np.ones((len(x_test), 1))], axis=-1)
# 随机初始化参数
theta = np.random.normal(size=X.shape[1])
# 随机梯度下降
# 为了观察迭代过程,我们记录每一次迭代后在训练集和测试集上的均方根误差
train_losses = []
test_losses = []
for i in range(num_epoch):
# 初始化批量生成器
batch_g = batch_generator(X, y_train, batch_size, shuffle=True)
train_loss = 0
for x_batch, y_batch in batch_g:
# 计算梯度
grad = x_batch.T @ (x_batch @ theta - y_batch)
# 更新参数
theta = theta - learning_rate * grad / len(x_batch)
# 累加平方误差
train_loss += np.square(x_batch @ theta - y_batch).sum()
# 计算训练和测试误差
train_loss = np.sqrt(train_loss / len(X))
train_losses.append(train_loss)
test_loss = np.sqrt(np.square(X_test @ theta - y_test).mean())
test_losses.append(test_loss)
# 输出结果,绘制训练曲线
print('回归系数:', theta)
return theta, train_losses, test_losses
# 设置迭代次数,学习率与批量大小
num_epoch = 20
learning_rate = 0.01
batch_size = 32
# 设置随机种子
np.random.seed(0)
_, train_losses, test_losses = SGD(num_epoch, learning_rate, batch_size)theta = theta - learning_rate * grad / len(x_batch)算出的梯度是一个批的,所以要除一下大小
学习率:
下山的方向是梯度方向,学习率则是我下山的步长
学习率增大,算法的收敛速度明显加快,下山速度更快
但是过大的学习率可能会让我在山陡峭的地方走太远的距离(learning rate * grad),导致错过我本想去的山谷
习题
1.C。1/x非线性
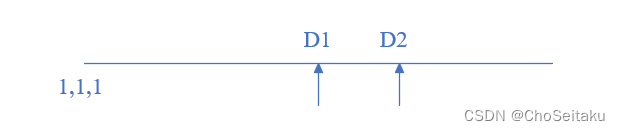
2.B。
3. 第二列×2 - 第一列 = 第三列,两个样本的特征线性相关,其行列式必为0,则X与X.T为0,不存在逆矩阵
第二列×2 - 第一列 = 第三列,两个样本的特征线性相关,其行列式必为0,则X与X.T为0,不存在逆矩阵
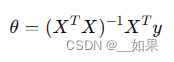
4.略
5.
-
过小的批量大小:
- 训练过程中需要更多的参数更新步骤,因此训练速度可能会变慢。
- 较小的批量可能无法充分利用计算资源,导致训练过程中的并行性较低,无法充分利用GPU等加速计算资源。
- 梯度的估计可能会更加不稳定,因为每个批量中的样本可能并不代表整个数据集的分布情况,这可能会导致训练过程中的震荡。
-
过大的批量大小:
- 训练过程中每个参数更新所使用的样本数目较多,因此训练速度可能会变慢,特别是在大规模数据集上。
- 较大的批量可能需要较大的内存来存储计算过程中的梯度信息和中间结果,这可能会导致内存不足或者性能下降。
- 过大的批量可能会导致训练过程中陷入局部极小值,因为每次参数更新所使用的样本数目较多,可能会限制参数空间的搜索范围。
6.增加一个控制代码
if abs(train_loss - prev_train_loss) < tol:
patience_count += 1
if patience_count >= patience:
print(f'达到终止条件,迭代停止,迭代次数:{i+1}')
break
else:
patience_count = 0
prev_train_loss = train_losstol 参数用于设置损失函数值的最小变化量,patience 参数用于设置连续迭代次数的容忍度。当连续 patience 次迭代中损失函数值变化量小于 tol 时,即终止迭代
混合策略:先确保一定执行N个epoch,后面再开始用控制代码