随想录日记part31
t i m e : time: time: 2024.03.29
主要内容:今天开始要学习动态规划的相关知识了,今天的内容主要涉及四个方面:
理论基础 ; 斐波那契数 ;爬楼梯 ;使用最小花费爬楼梯。
- 理论基础
- 509. 斐波那契数
- 70. 爬楼梯
- 746. 使用最小花费爬楼梯
关于动态规划的理论知识,我们可以直接去看 理论基础 对应的链接就可以了。下面主要还是对于题目的讲解。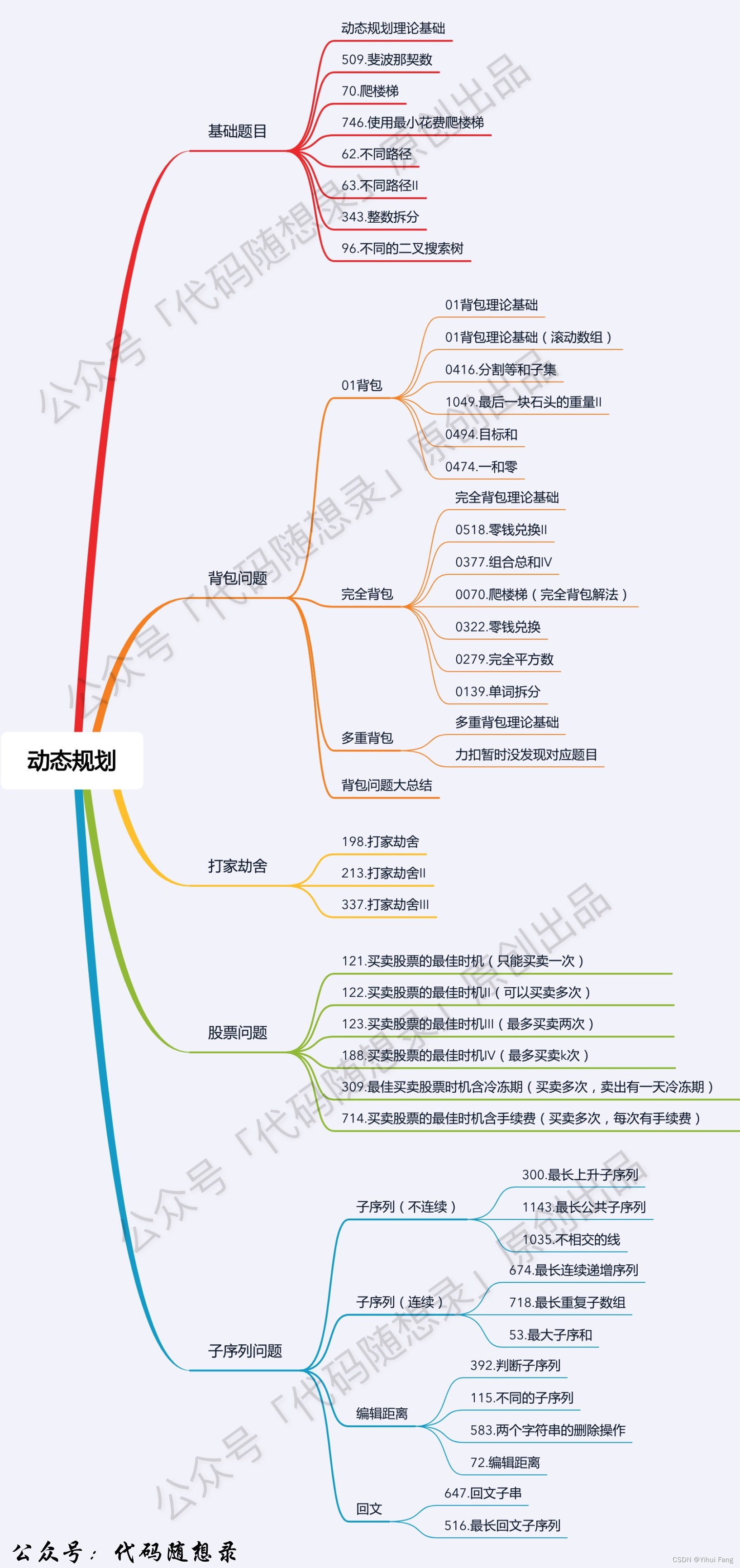
总结一下核心思想:
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
【1】.确定dp数组以及下标的含义
【2】.确定递推公式
【3】.dp数组如何初始化
【4】.确定遍历顺序
【5】.举例推导dp数组
Topic1斐波那契数
题目:
斐波那契数 (通常用 F ( n ) F(n) F(n) 表示)形成的序列称为斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F ( 0 ) = 0 , F ( 1 ) = 1 F(0) = 0,F(1) = 1 F(0)=0,F(1)=1
F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n) = F(n - 1) + F(n - 2) F(n)=F(n−1)+F(n−2),其中 n > 1 n > 1 n>1
给定 n n n ,请计算 F ( n ) F(n) F(n) 。
输入:
n
=
4
n = 4
n=4
输出:
3
3
3
解释:
F
(
4
)
=
F
(
3
)
+
F
(
2
)
=
2
+
1
=
3
F(4) = F(3) + F(2) = 2 + 1 = 3
F(4)=F(3)+F(2)=2+1=3
思路:
按照上面的五个步骤给出下面的代码:
代码如下:
class Solution {
public int fib(int n) {
// 【1】.确定dp数组以及下标的含义
int[] dp = new int[n + 1];// dp[n]就是第i个数的斐波那契数值
// 【3】.dp数组如何初始化
if (n == 0)
return 0;
if (n == 1)
return 1;
dp[0] = 0;
dp[1] = 1;
// 【2】.确定递推公式【4】.确定遍历顺序【5】.举例推导dp数组
for (int i = 2; i < n + 1; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
时间复杂度:
O
(
n
)
O(n)
O(n)
空间复杂度:
O
(
n
)
O(n)
O(n)
Topic2爬楼梯
题目:
假设你正在爬楼梯。需要 n n n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
输入:
n
=
3
n = 3
n=3
输出:
3
3
3
解释:
有三种方法可以爬到楼顶。
【1】.1 阶 + 1 阶 + 1 阶
【2】. 1 阶 + 2 阶
【3】. 2 阶 + 1 阶
思路:
按照上面的五个步骤给出下面的代码,在注释中给出具体的思路:
整体代码如下:
class Solution {
public int climbStairs(int n) {
// 【1】.确定dp数组以及下标的含义,这里的dp[i]表示i阶到达楼顶的方法数
int[] dp = new int[n + 1];
// 【3】.dp数组如何初始化
if (n == 1)
return 1;
if (n == 2)
return 2;
dp[1] = 1;
dp[2] = 2;
// 【2】.确定递推公式dp[i]=dp[i-1]+dp[i-2];【4】.确定遍历顺序【5】.举例推导dp数组
for (int i = 3; i < n + 1; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
时间复杂度:
O
(
n
)
O(n)
O(n)
空间复杂度:
O
(
n
)
O(n)
O(n)
Topic3使用最小花费爬楼梯
题目:
给你一个整数数组 c o s t cost cost ,其中 c o s t [ i ] cost[i] cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。
输入:
c
o
s
t
=
[
10
,
15
,
20
]
cost = [10,15,20]
cost=[10,15,20]
输出:
15
15
15
解释: 你将从下标为 1 的台阶开始。支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
思路:
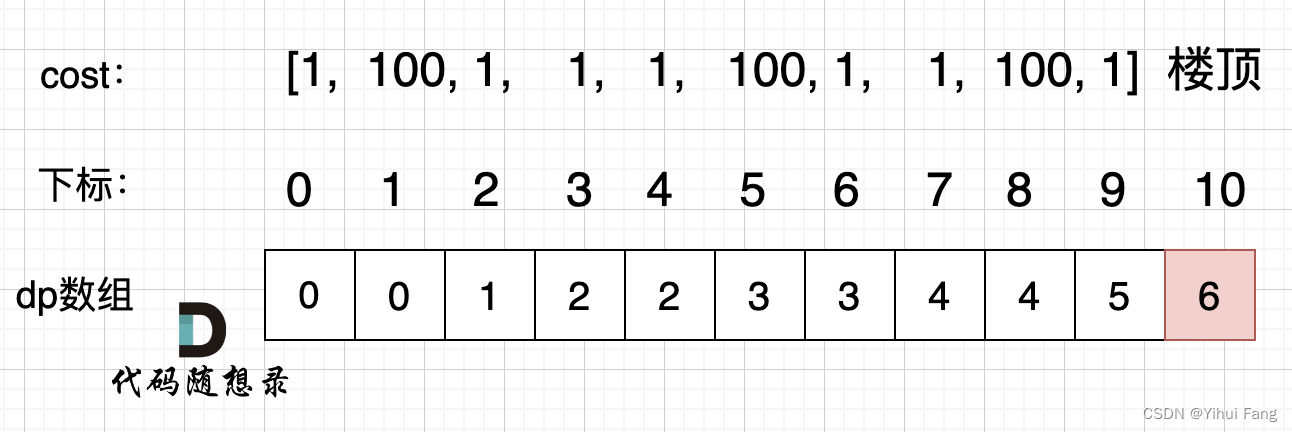
举例推导dp数组
拿示例: c o s t = [ 1 , 100 , 1 , 1 , 1 , 100 , 1 , 1 , 100 , 1 ] cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] cost=[1,100,1,1,1,100,1,1,100,1] ,来模拟一下 d p dp dp 数组的状态变化,如下:
整体代码如下:
class Solution {
public int minCostClimbingStairs(int[] cost) {
// 【1】.确定dp数组以及下标的含义
// dp[i]表示到达第i个台阶的最低花费钱数
int n = cost.length;
int[] dp = new int[cost.length + 1];
// 【3】.dp数组如何初始化【4】.确定遍历顺序
dp[0] = 0;
dp[1] = 0;
// 【2】.确定递推公式//【4】.确定遍历顺序//【5】.举例推导dp数组
for (int i = 2; i < n + 1; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[n];
}
}
时间复杂度:
O
(
n
)
O(n)
O(n)
空间复杂度:
O
(
n
)
O(n)
O(n)









![[InternLM训练营第二期笔记]1. 书生·浦语大模型全链路开源开放体系](https://img-blog.csdnimg.cn/direct/9bb7976488ec478c93293937d9284afb.png)