蓝桥杯第十二届省赛真题-分果果
题目描述
小蓝要在自己的生日宴会上将 n 包糖果分给 m 个小朋友。每包糖果都要分出去,每个小朋友至少要分一包,也可以分多包。
小蓝将糖果从 1 到 n 编号,第 i 包糖果重 wi。小朋友从 1 到 m 编号。每个小朋友只能分到编号连续的糖果。小蓝想了很久没想出合适的分配方案使得每个小朋友分到的糖果差不多重。为了更好的分配糖果可以再买一些糖果,让某一些编号的糖果有两份。当某个编号的糖果有两份时,一个小朋友最多只能分其中的一份。请找一个方案,使得小朋友分到的糖果的最大重量和最小重量的差最小,请输出这个差。
如,小蓝现在有 5 包糖果,重量分别为 6, 1, 2, 7, 9,如果小蓝要分给两个小朋友,则他可以将所有糖果再买一份,两个小朋友都分到 1 至 5 包糖果,重量都是 25,差为 0。
如,小蓝现在有 5 包糖果,重量分别为 6, 1, 2, 7, 9,如果小蓝要分给三个小朋友,则他可以将第 3 包糖果再买一份,第一个小朋友分 1 至 3 包,第二个小朋友分 3 至 4 包,第三个小朋友分第 5 包,每个小朋友分到的重量都是 9,差为 0。
如,小蓝现在有 5 包糖果,重量分别为 6, 1, 2, 7, 9,如果小蓝要分给四个小朋友,则他可以将第 3 包和第 5 包糖果再买一份,仍然可以每个小朋友分到的重量都是 9,差为 0。
如,小蓝现在有 5 包糖果,重量分别为 6, 1, 2, 7, 9,如果小蓝要分给五个小朋友,则他可以将第 4 包和第 5 包糖果再买一份,第一个小朋友分第 1 至 2 包重量为 7,第二个小朋友分第 3 至 4 包重量为 9,第三个小朋友分第 4 包重量为 7,第四个和第五个小朋友都分第 5 包重量为 9。差为 2。
输入格式
输入第一行包含两个整数 n 和 m,分别表示糖果包数和小朋友数量。
第二行包含 n 个整数 w1, w2, · · · , wn,表示每包糖果的重量。
输出格式
输出一个整数,表示在最优情况下小朋友分到的糖果的最大重量和最小重量的差。
样例输入
5 2 6 1 2 7 9
样例输出
0
提示
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ n ≤ 10,1 ≤ m ≤ 10,1 ≤ wi ≤ 10;
对于 60% 的评测用例,1 ≤ n ≤ 30,1 ≤ m ≤ 20,1 ≤ wi ≤ 30;
对于所有评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 50,1 ≤ wi ≤ 100。在评测数据中,wi 随机生成,在某个区间均匀分布。
代码表示
#include <stdio.h>
#include <string.h>
int dp[51][101][101], W[101], n, m, ans = 0x3F3F3F3F;
int max(int arg1, int arg2) { return arg1 > arg2 ? arg1 : arg2; }
int min(int arg1, int arg2) { return arg1 < arg2 ? arg1 : arg2; }
int main() {
memset(dp, 0x3F, sizeof dp);
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &W[i]), W[i] += W[i - 1];
dp[0][0][0] = 0;
for (int minW = W[n] * 2 / m; minW > 0; minW--) {
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++) {
int trans2 = 0, trans3 = 0;
for (int k = 1; k <= j; k++) {
dp[i][j][k] = dp[i][j][k - 1];
while (trans2 < k && W[j] - W[trans2 + 1] >= minW &&
max(dp[i - 1][trans2 + 1][trans2 + 1], W[j] - W[trans2 + 1]) <= max(dp[i - 1][trans2][trans2], W[j] - W[trans2])) trans2++;
if (W[j] - W[trans2] >= minW)
dp[i][j][k] = min(dp[i][j][k], max(dp[i - 1][trans2][trans2], W[j] - W[trans2]));
while (trans3 < k && W[j] - W[trans3 + 1] >= minW &&
max(dp[i - 1][k][trans3 + 1], W[j] - W[trans3 + 1]) <= max(dp[i - 1][k][trans3 + 1], W[j] - W[trans3])) trans3++;
if (W[j] - W[trans3] >= minW)
dp[i][j][k] = min(dp[i][j][k], max(dp[i - 1][k][trans3], W[j] - W[trans3]));
}
}
ans = min(ans, dp[m][n][n] - minW);
}
printf("%d\n", ans);
}
难难难好难!
[蓝桥杯 2018 省 B] 螺旋折线
题目描述
如图所示的螺旋折线经过平面上所有整点恰好一次。
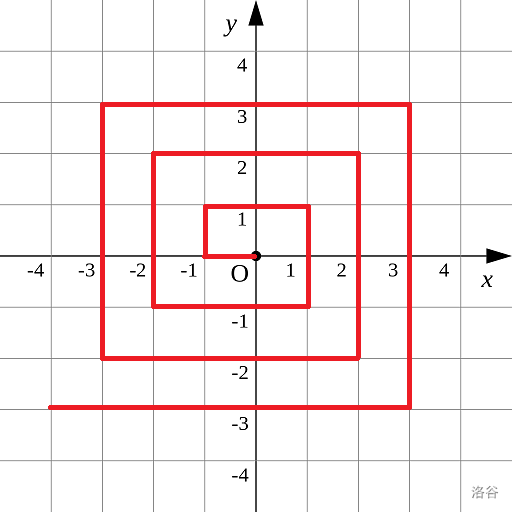
对于整点 (X,Y),我们定义它到原点的距离 dis(X,Y) 是从原点到 (X,Y) 的螺旋折线段的长度。
例 dis(0,1)=3,dis(−2,−1)=9。
给出整点坐标 (X,Y),你能计算出dis(X,Y) 吗?
输入格式 X 和 Y
输出格式 输出dis(X,Y)
样例:
输入 0 1
输出 3
说明/提示
对于 40%的数据,−1000≤X,Y≤1000。
对于 70% 的数据,−105≤X,Y≤105。
对于 100% 的数据,−109≤X,Y≤109。
代码表示
#include <stdio.h>
int max(int a,int b)
{
return a>b?a:b;
}
int main()
{
long long x,y,t,ans=0;
scanf("%lld%lld",&x,&y);
if (x>=0&&y>=0) // 第1象限
{
t=max(x,y);
ans=4*t*t+x-y;
}
else if (x<0&&y>=0) // 第2象限
{
t=max(-x,y);
ans=2*t*(2*t-1)+x+y;
}
else if (x>=0&&y<0) // 第4象限
{
t=max(x,-y);
ans=2*t*(2*t+1)-x-y;
}
else // 第3象限
{
if (x+1<y)
t=-x-x-1;
else
t=-y-y+1;
ans=t*t-x+y-1;
}
printf("%lld\n",ans);
return 0;
}
思路提示
本题属于找规律的问题,关键是找出规律。
先观察题目描述中的图示,从原点出发,第 1 步向左走 1 个单位至 (−1,0) 后转折,第 2 步向上走 1 个单位到 (−1,−1) 后转折,第 3 步向右走 2 个单位至 (1,1) 后转折,第 4 步向下走 2 个单位至 (1,−1) 后转折,…,之后按上面的循环不断走下去。每走两步后,每步所走的单位数加 1。即每步所走的单位数序列为1,1,2,2,3,3,4,4,…。
1)第 1 象限整点的规律。
先考察第 1 象限的转折点,该点横坐标和纵坐标值相等。
从原点出发走 3 步,可到达转折点 (1,1),dist(1,1)=1+1+2=4。
从原点出发走 7 步,可到达转折点 (2,2),dist(2,2)=1+1+2+2+3+3+4=16。
一般地,从原点出发走 4×a−1 步可以达到转折点(a,a),这 4×a−1 步中,前4×a−2 步每两步是同一个单位,最后一步为2×a 个单位。
dist(a,a)=1+1+2+2+…+(2×a−1)+(2×a−1)+2×a=4×a2。
对于第 1 象限的其他非转折点的整点(a,b),这里 a≠b。
若 a<b,则在直线 y=b 上,点(a,b) 向右走b−a 个单位可以到达转折点(b,b)。因此,
dist(a,b)=dist(b,b)−(b−a)=4×b2+a−b。
若 a>b,则在直线x=a 上,从转折点(a,a) 再向下走a−b 个单位就可以达到点(a,b)。因此,
dist(a,b)=dist(a,a)+(a−b)=4×a2+a−b。
若设 t=max(a,b),则上面的规律可以统一表为dist(a,b)=4×t2+a−b。
2)第 2 象限整点的规律。
从原点出发走 2 步可以到达转折点(−1,1),dist(−1,1)=1+1=2。
从原点出发走 6步可以到达转折点 (−2,2),dist(−2,2)=1+1+2+2+3+3=12。
一般地,从原点出发走 4×a−2 步可以达到转折点(−a,a),dist(−a,a)=1+1+2+2+…+(2×a−1)+(2×a−1)=4×a2−2×a。
对于第 2 象限的其他非转折点的整点(−a,b),这里a>0,b>0 且 −a≠b。
若 −a<b,则在直线y=b 上,从转折点(−b,b) 向右走b−a 个单位可以到达(−a,b)。所以,dist(−a,b)=dist(−b,b)+(b−a)=4×b2−2×b+(−a)+b。
若−a>b,则在直线x=−a 上,从整点 (−a,b) 再向上走a−b 个单位就可以达到转折点 (−a,a)。因此,dist(−a,b)=dist(−a,a)−(a−b)=4×a2−2×a+(−a)+b。
若设 t=max(a,b),则第 2 象限的规律可以统一表示为dist(−a,b)=4×t2t−2×t+(−a)+b。
3)第 4 象限整点的规律。
同上理,若设t=max(a,−b),则第 4 象限整点 (a,b) 的规律可以统一表示为dist(a,b)=4×t2+2×t−a−b。这里a>0,b<0。
4)第 3象限整点的规律。
第 3 象限整点的规律略微麻烦一些。 从原点出发走 1 步可以到达转折点(−1,0),dist(−1,0)=1。
从原点出发走 5 步可以到达转折点 (−2,−1),dist(−2,−1)=1+1+2+2+3=9。
一般地,从原点出发走4×a−3 步可以达到转折点dist(−a,−a+1)=1+1+2+2+…+(2×a−2)+(2×a−2)+(2×a−1)=(2×a−1)2。
对于第 3 象限的其他非转折点的整点(a,b),这里a<0,b<0 且 a+1≠b。
将第 3 象限的转折点用一条直线连起来,则直线方程为 y=x+1。
若 a+1<b,则其在直线y=x+1 的上方,这样在直线x=a 上从转折点(a,a+1) 向上走−a−1+b 个单位可以到达(a,b)。因此dist(a,b)=dist(a,a+1)+(b−a−1)=[2×(−a)−1]2+b−a−1。
若 a+1>b,则其在直线y=x+1 的下方,这样在直线y=b 上从整点(a,b) 再向左走a+1−b 个单位就可以达到转折点(b−1,b)。因此dist(−a,b)=dist(b−1,b)−(a+1−b)=[2×(−b+1)−1]2+b−a−1。
呜呜呜呜呜这规律是能该找到的吗
[蓝桥杯 2021 省 B] 时间显示
题目描述
小蓝要和朋友合作开发一个时间显示的网站。在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从 1970 年 1 月 1 日 00:00:00 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
输入格式
输入一行包含一个整数,表示时间。
输出格式
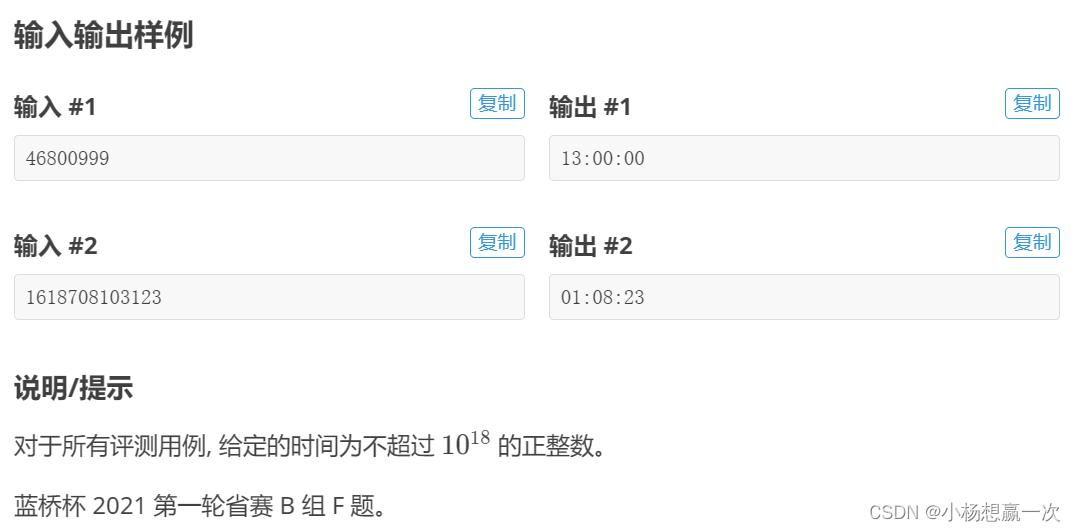
输出时分秒表示的当前时间, 格式形如HH:MM:SS, 其中 HH 表示时, 值为 0 到 23,MM 表示分。值为 0 到 59。SS 表示秒, 值为 0 到 59。时、分、秒不足两位时补前导 0。
代码表示
#include <bits/stdc++.h>
using namespace std;
int main() {
long long n;//毫秒数
scanf("%lld", &n);
n /= 1000;//忽略不足1秒的毫秒数
printf("%02lld:%02lld:%02lld\n", n % 86400 / 3600, n % 3600 / 60, n % 60);
return 0;
}心得体会
1、计算出时、分、秒。其中时可以用 n%86400/3600 来表示,分可以用 n%3600/60 来表示,秒可以用 n%60 来表示。这里的 86400 秒是一天 24 小时内所经过的秒数,3600 秒是 1 小时内所经过的秒数,60 秒是 1 分钟内所经过的秒数。
2、这类题我们通过测试用例来计算得到具体使用的是%还是 /
3、%02lld"是一个格式化字符串,它的组成部分有:
%:表示一个占位符的开始。0:表示如果输出的整数不足指定宽度时,用0来填充。2:表示输出的整数宽度至少为2位。lld:表示要输出的整数是long long类型的。
[蓝桥杯 2017 省 B] k 倍区间
题目描述
给定一个长度为 N 的数列,A1,A2,⋯AN,如果其中一段连续的子序列Ai,Ai+1,⋯Aj(i≤j) 之和是 K 的倍数,我们就称这个区间[i,j] 是 K 倍区间。
你能求出数列中总共有多少个 K 倍区间吗?
输入格式
第一行包含两个整数 N 和 K(1≤N,K≤10^5)。
以下 N 行每行包含一个整数 Ai(1≤Ai≤10^5)。
输出格式
输出一个整数,代表 K 倍区间的数目。
代码表示
第一种:暴力
会超时间,想不到只能这样写,具体的核心点在从位置 i 开始遍历到位置 j"时,可以通过一个具体的数列来解释。假设我们有一个数列 [1, 2, 3, 4, 5],并且我们想计算所有可能的子序列的和。在这个例子中,外部循环变量 i 表示子序列的起始位置,内部循环变量 j 表示子序列的结束位置。以下是通过具体例子来解释代码的执行过程:
1、当 i 等于 0 时,表示我们从位置 0 开始作为子序列的起始位置。内部循环从 j = i 开始,即 j = 0。
第一次内部循环迭代:j 等于 0,当前子序列为 [1],和为 1。
第二次内部循环迭代:j 等于 1,当前子序列为 [1, 2],和为 3。
第三次内部循环迭代:j 等于 2,当前子序列为 [1, 2, 3],和为 6。
第四次内部循环迭代:j 等于 3,当前子序列为 [1, 2, 3, 4],和为 10。
第五次内部循环迭代:j 等于 4,当前子序列为 [1, 2, 3, 4, 5],和为 15。
2、当 i 等于 1 时,表示我们从位置 1 开始作为子序列的起始位置。内部循环从 j = i 开始,即 j = 1。
第一次内部循环迭代:j 等于 1,当前子序列为 [2],和为 2。
第二次内部循环迭代:j 等于 2,当前子序列为 [2, 3],和为 5。
第三次内部循环迭代:j 等于 3,当前子序列为 [2, 3, 4],和为 9。
第四次内部循环迭代:j 等于 4,当前子序列为 [2, 3, 4, 5],和为 14。
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, i, j;
long long k, ann = 0, num = 0;
cin >> n >> k;
long long arr[n];
for (i = 0; i < n; ++i) {
cin >> arr[i];
num += arr[i];
}
if (num % k == 0) {
ann++;
}
//外部循环变量 i 用于指定子序列的起始位置
//内部循环变量 j 用于指定子序列的结束位置。
for (i = 0; i < n; ++i) {
long long sum = 0;
for (j = i; j < n; ++j) {
sum += arr[j];
if (sum % k == 0) {
ann++;
}
}
}
cout << ann << endl;
return 0;
}第二种:前缀和
根据范围可得知暴力会直接超时。那有没有别的快速思路呢?当然有!利用同余定理:当 amodk=bmodk 时,∣a−b∣modk=0。若设前缀和数组为 s,则我们知道,si 就表示 a0+a1+a2+...+ai,那么我们用另一个数组存储每个前缀和的模数,当找到相同模数时,中间的那段即为 k 的倍数。
对于第二个循环,也是前缀和重要的部分:
1、循环变量 i 从 0 到 n 遍历,用于遍历前缀和数组 s。
2、在循环的每一次迭代中,执行以下操作:
1)s[i] % k:计算前缀和 s[i] 除以 k 的余数。这个余数表示了从数列的开头到位置 i 的前缀和除以 k 后的剩余部分。
2)xb[s[i] % k]:通过索引 s[i] % k,访问模数计数器 xb 中对应余数的计数器值。这个值表示之前出现相同余数的次数。
3)ans += xb[s[i] % k]:将之前出现相同余数的次数累加到答案 ans 中。这表示在位置 i 之前,存在多少个前缀和的余数与当前位置 i 的前缀和余数相同,从而形成了多少个区间的和为 k 的倍数。
4)xb[s[i] % k]++:将当前余数的计数器值加 1,以记录出现相同余数的次数。
3、循环结束后,答案 ans 就表示了整个数列中和为 k 的倍数的区间个数。
#include<bits/stdc++.h>
#define int long long
using namespace std;
//s前缀和数组,xb用于存储模数
int n,k,s[100005],ans=0,xb[100005];
signed main(){
cin>>n>>k;
//整数 t,将其赋值给 s[i],并更新 s[i] 的值
//为前一个前缀和 s[i-1] 加上当前读取的元素 t
//s[i] 存储了数列中前 i 个元素的和。
for(int i=1,t;i<=n;i++)
cin>>t,s[i]=s[i-1]+t;
for(int i=0;i<=n;i++)//注意!必须从0开始
//有n个模数相同中间就有(n-1)段和为k的倍数
ans+=xb[s[i]%k]++;
cout<<ans;
return 0;
}注意:
xb[s[i] % k] 是通过索引 s[i] % k 来访问模数计数器 xb 中对应余数的计数器值。这个值表示之前出现相同余数的次数。
原理是利用哈希表来实现模数计数器。哈希表是一种数据结构,它可以通过将键映射到值的方式来存储和访问数据。我们使用哈希表来存储余数和对应的计数器值。
[蓝桥杯 2022 省 A] 求和
题目描述
给定 n 个整数 a1,a2,⋯,an, 求它们两两相乘再相加的和,即
S=a1⋅a2+a1⋅a3+⋯+a1⋅an+a2⋅a3+⋯+an−2⋅an−1+an−2⋅an+an−1⋅an
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数a1,a2,⋯an 。
输出格式
输出一个整数 S,表示所求的和。请使用合适的数据类型进行运算。

代码表示
第一想法:暴力
刚开始这不就是暴力吗,而且暴的时候还得注意
①定义a[n] 的时候要再输入n之后。②用到什么变量的时候再来对其进行定义,而且num这种要记得对它初始化。
但这系列工作做完也只有30分。代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
long long n,i,j;
cin>>n;
long long a[n];
for(i=0;i<n;++i){
cin>>a[i];
}
int num=0;
for(i=0;i<n;++i){
for(j=i+1;j<n;++j){
num+=a[i]*a[j];
}
}
cout<<num;
return 0;
}第二正解:前缀和算法
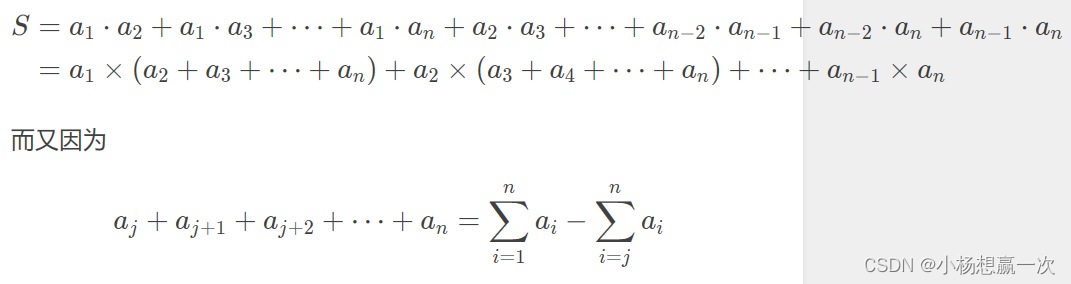
注意数据范围。十年 OI 一场空,不开 long long 见祖宗!
#include<bits/stdc++.h>
using namespace std;
int n;
long long a[200010],b[200010];
long long sum=0;
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
b[i]=b[i-1]+a[i];
}
for(int i=1;i<n;i++){
sum+=a[i]*(b[n]-b[i]);
}
cout<<sum<<endl;
return 0;
}关于前缀和的讲解
例一:

解题:递推:B[0] = A[0],对于i >=1则 B[i] = B[i-1] + A[i]。
#include <iostream>
using namespace std;
int N, A[10000], B[10000];
int main() {
cin >> N;
for (int i = 0; i < N; i++) {
cin >> A[i];
}
// 前缀和数组的第一项和原数组的第一项是相等的。
B[0] = A[0];
for (int i = 1; i < N; i++) {
// 前缀和数组的第 i 项 = 原数组的 0 到 i-1 项的和 + 原数组的第 i 项。
B[i] = B[i - 1] + A[i];
}
for (int i = 0; i < N; i++) {
cout << B[i] << " ";
}
return 0;
}例二:【深进1.例1】求区间和

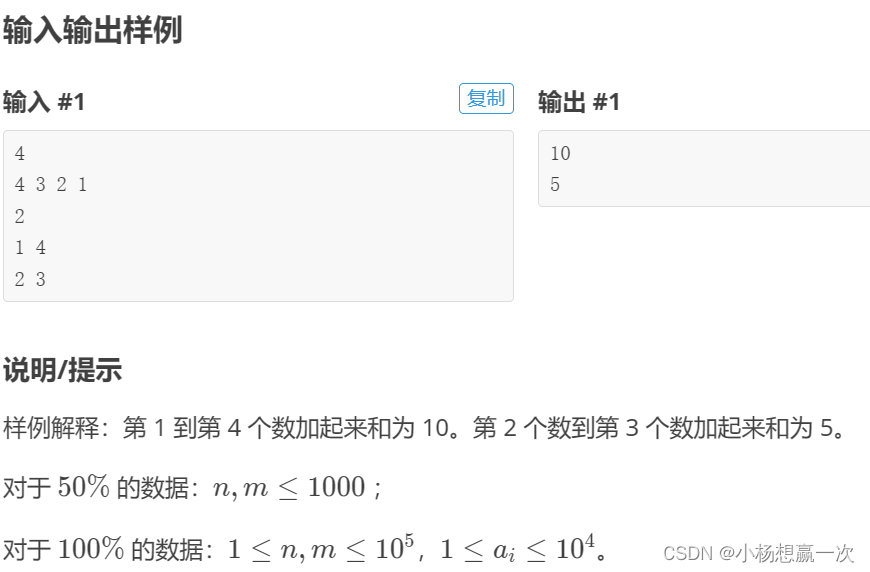
题解:前缀和差分模板题。

#include<bits/stdc++.h>
using namespace std;
// 定义一个快速读取整数的函数
inline int read()
{
int x = 0; // 保存读取的整数
int f = 1; // 符号标志,默认为正数
char ch = getchar(); // 读取字符
// 跳过非数字字符,如果遇到负号,则将符号标志置为 -1
while (!isdigit(ch)) {
if (ch == '-')
f = -1;
ch = getchar();
}
// 循环读取连续的数字字符,并将其转换为整数
while (isdigit(ch)) {
x = x * 10 + ch - '0'; // 将当前数字字符转换为对应的整数,并累加到 x
ch = getchar(); // 继续读取下一个字符
}
return x * f; // 返回最终的整数值
}
int n, m, a[100050], s[100050];
int main()
{
n = read(); // 读取输入的 n
// 计算前缀和数组 s,并同时读取输入的 n 个整数到数组 a
for (int i = 1; i <= n; i++)
s[i] = s[i - 1] + (a[i] = read());
m = read(); // 读取输入的 m
// 计算 m 个区间的区间和
for (int i = 1; i <= m; i++) {
int l = read(); // 读取区间的左边界 l
int r = read(); // 读取区间的右边界 r
// 输出区间和 s[r] - s[l-1]
cout << s[r] - s[l - 1] << endl;
}
return 0;
}[蓝桥杯 2023 省 A] 填空题1
题目描述
A. 幸运数
小蓝认为如果一个数含有偶数个数位,并且前面一半的数位之和等于后面一半的数位之和,则这个数是他的幸运数字。例如2314 是一个幸运数字,因为它有 4 个数位,并且2+3=1+4。现在请你帮他计算从 1 至100000000 之间共有多少个不同的幸运数字。
4430091
代码表示
#include<bits/stdc++.h>
using namespace std;
bool check(int x){
int tmp=x,len=0;
//每次循环将 tmp 除以 10,将 len 的值加一,直到 tmp 变为 0。
//这个循环的目的是计算整数 x 的位数
while(tmp){
len++;
tmp/=10;
}
if(len%2==1)//基数则不考虑
return 0;
int t=len/2,ans1=0,ans2=0;
//前半部分位数的数字逐个取出
while(t--){
ans1+=x%10;//取出 x 的个位数
x/=10;//去除个位数
}
//将 x 的剩余部分位数的数字逐个取
while(x){
ans2+=x%10;
x/=10;
}
return ans1==ans2;
}
int main(){
int ans=0;
for(int i=10;i<=100000000;i++){
if(check(i))
ans++;
}
cout<<ans;
return 0;
}心得体会
1、字符串某个值转具体值的时候num1+=arr[i]-'0';要记得减 ’0‘
2、清空原来字符串 arr.clear();字符串的名字叫做arr
3、原来不用字符串也是可以的!!
对于x:取出 x 的个位数存入ans1 :ans1+=x%10; 去除个位数:x/=10;
4、函数头:bool check(int x){........} 调用:check(i)
整体的效果:if( check(i) ) { ans++; } cout<<ans;
5、活用while,真的很妙!