首先是组合逻辑电路考虑的是竞争冒险,冒险会产生毛刺。重点研究如何去毛刺
时序逻辑电路考虑的是时序不满足会产生的亚稳态问题:如何考量时序满不满足呢?根据不同的场景又有不同的说法。
时序分析的两组基本概念
- 建立时间与保持时间
1.在同步系统和异步系统(跨时钟域传输)中有两个时间概念:建立时间、保持时间。
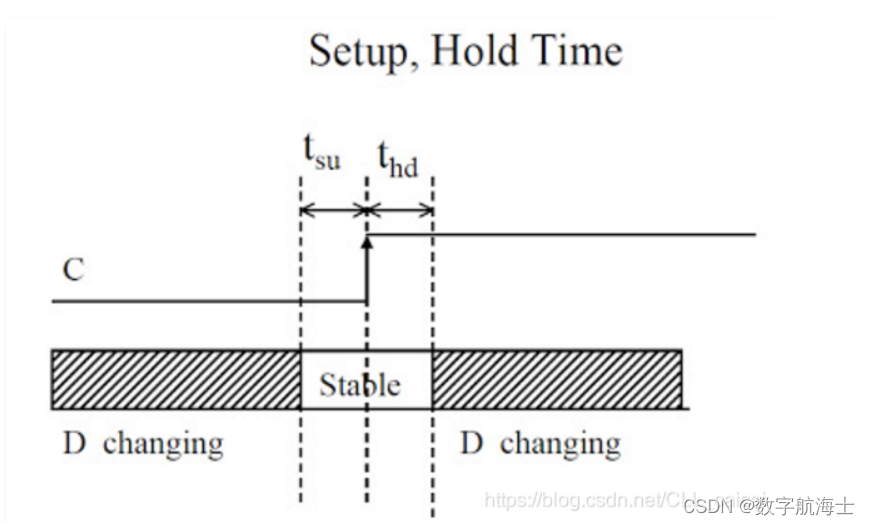
触发器在时钟上升沿来临时对数据进行采样,产生对应的输出。但是实际器件无法瞬时完成数据采样这一过程,需要数据在时钟沿前后均稳定一定时间,即引入了(触发器的)建立时间与保持时间这一概念。
建立时间Tsu:时钟有效沿到来之前数据必须保持稳定的最小时间;
保持时间Th:时钟有效沿到来之后数据必须保持稳定的最小时间;
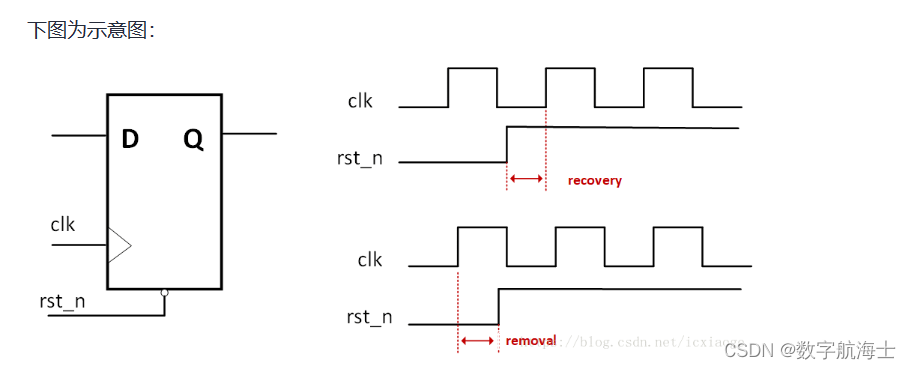
- 恢复时间、去除时间
2.针对异步控制信号(主要是复位信号)中有两个时间概念:恢复时间、去除时间。
恢复时间(Recovery Time)是指异步控制信号(如寄存器的异步清除和置位控制信号)在“下个时钟沿”来临之前变无效的最小时间长度。这个时间的意义是,如果保证不了这个最小恢复时间,也就是说这个异步控制信号的解除与“下个时钟沿”离得太近(但在这个时钟沿之前),没有给寄存器留有足够时间来恢复至正常状态,那么就不能保证“下个时钟沿”能正常作用,也就是说这个“时钟沿”可能会失效。与同步电路中的建立时间类似
去除时间(Removal)是指异步控制信号(如寄存器的异步清除和置位控制信号)在“有效时钟沿”之后变无效的最小时间长度。这个时间的意义是,如果保证不了这个去除时间,也就是说这个异步控制信号的解除与“有效时钟沿”离得太近(但在这个时钟沿之后),那么就不能保证有效地屏蔽这个“时钟沿”,也就是说这个“时钟沿”可能会起作用。与同步电路中的保持时间类似
换句话来说,如果你想让某个时钟沿起作用,那么你就应该在“恢复时间”之前是异步控制信号变无效,如果你想让某个时钟沿不起作用,那么你就应该在“去除时间”过后使控制信号变无效。如果你的控制信号在这两种情况之间,那么就没法确定时钟沿是否起作用或不起作用了,也就是说可能会造成寄存器处于不确定的状态。而这些情况是应该避免的。所以恢复时间和去除时间是应该遵守的。
一:到底是什么是亚稳态?
定义:如果触发器的输入电压采样时间过短,即时序不够,则触发器需要花很长时间来实现输出逻辑达到标准电平,也就是说,电路处于中间态的时间变长,使得电路“反应”迟钝,这就是“亚稳态”。(例如输入信号在时钟有效沿的建立时间和保持时间之间改变了,导致不满足触发器的建立时间或保持时间,导致输出有一段时间的不稳定态,就是亚稳态。)
但是还有一种说法:
亚稳态是触发器的一个固有特性,正常采样也会有一个亚稳态时间。当建立时间和保持时间满足时,触发器会经历采样,亚稳态后,进入一个正确的状态。
这句话值得斟酌,亚稳态是触发器的固有特性,是触发器需要经历的过程,但是正常采样,即使会有一个亚稳态时间,但是亚稳态后,会进入一个正确的状态。
于此对比,也即是非正常采样时的亚稳态之后的固定电平不一定是一个正确的状态。

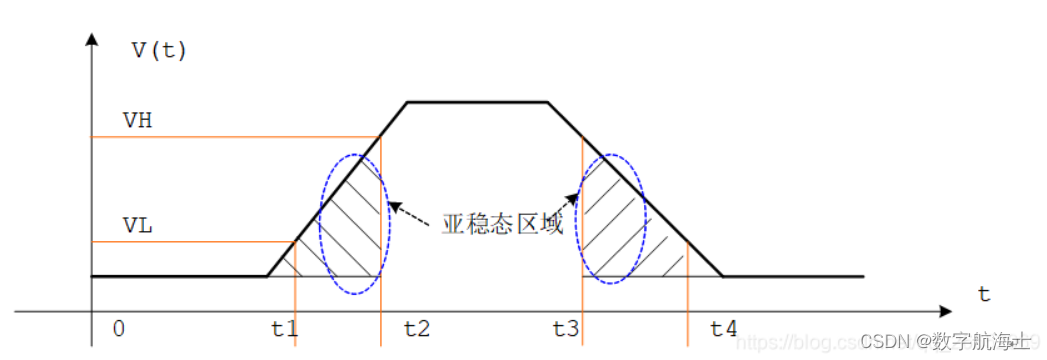
电平上的表现:
数字电路中,对于电平小于电压阈值 VL的称为0,大于电压阈值VL 称之为1,而对于从0到1之间跳变或从1到0之间跳变期间叫做系统的亚稳态。
后果:
1、亚稳态中间态时间变长:亚稳态是触发器的一个固有特性,正常采样也会有一个亚稳态时间。当建立时间和保持时间满足时,触发器也会经历采样---亚稳态---随后稳定输出。而出现亚稳态问题时,亚稳态(中间态)时间变长。
2、亚稳态的输出不一定正确:正常工作时,触发器经历较短的亚稳态时间,随后会正确输出;而出现亚稳态问题时,触发器经历较长的亚稳态时间,最终输出稳定但无法保证正确(是稳定的标准电平信号,但难以保证是输入对应输出);
工程意义:
亚稳态是指触发器无法在某个规定的时间内达到可以确认的状态。一旦触发器进入亚稳态,则既无法预测触发器的输出电平,也无法预测什么时候稳定在某个确认的电平上。(稳定所需时间不定、输出结果不定)
二:亚稳态产生的原因
1.不满足建立时间或者是保持时间
同步系统中可能会满足时序,因此可能产生亚稳态。(在这里不做分析了)
首先在同步逻辑中只要STA分析过了正常是不会遇到亚稳态问题的。由于在同步逻辑中STA分析以及保证了每个触发器都能满足自己的建立时间以及保持时间。在时序分析课程中会专门讨论这个问题。
因此在专门分析亚稳态的时候不考虑这种情况。所以我们认为同步系统中,输入总是与时钟同步,因此寄存器的setup time和hold time是满足的,一般情况下是不会发生亚稳态情况的。
异步系统也可能不满足时序,因此也可能产生亚稳态。(在这里重点分析)

造成在第二个触发器的Dout输出端输出高电平与低电平之间的一个不稳定状态(亚稳态)。该实例传递信号为单比特信号,对快时钟域的影响一般在捕获数据不正确、寄存器无法正常操作以及也会出现异步复位产生的那些问题。对于多比特数据而言(一般在数据采集,用作数据总线),造成采集数据错误。
2.不满足恢复时间和去除时间
这里一般指的是复位的时候。包括了异步复位和同步复位
1:异步复位通常会存在亚稳态的隐患
如下图所示,复位信号与时钟信号没有任何关系,不在同一时钟域中,显然复位信号与时钟信号是异步关系,异步复位逻辑。

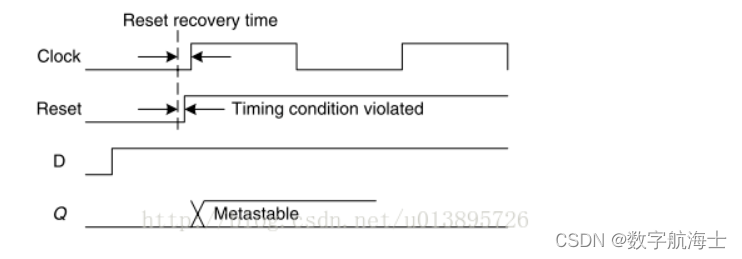
Recovery违例,(复位无效状态离时钟上升沿太近,触发器来不及恢复正常状态)在这种情况下,由上图明显看出来,触发器会进入亚稳态。
同步复位:
直接给出同步复位的RTL电路:

当输入端din为高电平的时候,复位信号的撤销正好位于setup 和 hold之间,那么与din相与之后的信号也在clk信号的setup和hold之间,亚稳态肯定也随之产生。这种情况下的同步复位是失败的。整个过程如下图所示:
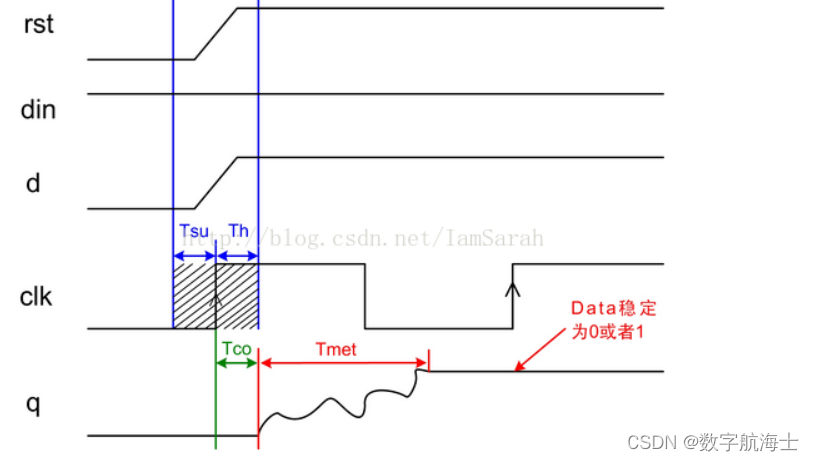
三:亚稳态的解决办法
亚稳态是复杂时序电路中无法避免的现象,设计电路时首先要减少亚稳态发生的概率,其次要使系统对产生的错误不敏感。
前者靠同步来实现,后者需要根据不同的设计应用采取不同的处理办法。
0.对于同步系统的时序违例进行时序优化
1.对于跨时钟域信号的处理
a.对异步信号进行同步处理
b.采用FIFO对跨时钟信号进行缓冲设计
2.对于复位信号的处理
c.对复位信号采用异步复位、同步处理的方法
这三种处理方法其实本质上都是在进行同步处理, 也就是运用同步器进行处理。而同步器的一般设计方法就是把将两个触发器级联,第一个触发器看做预处理器,主要是对数据进行缓冲,使得数据在传入第二个触发器之前稳定下来。
原文链接:https://blog.csdn.net/CLL_caicai/article/details/104625791