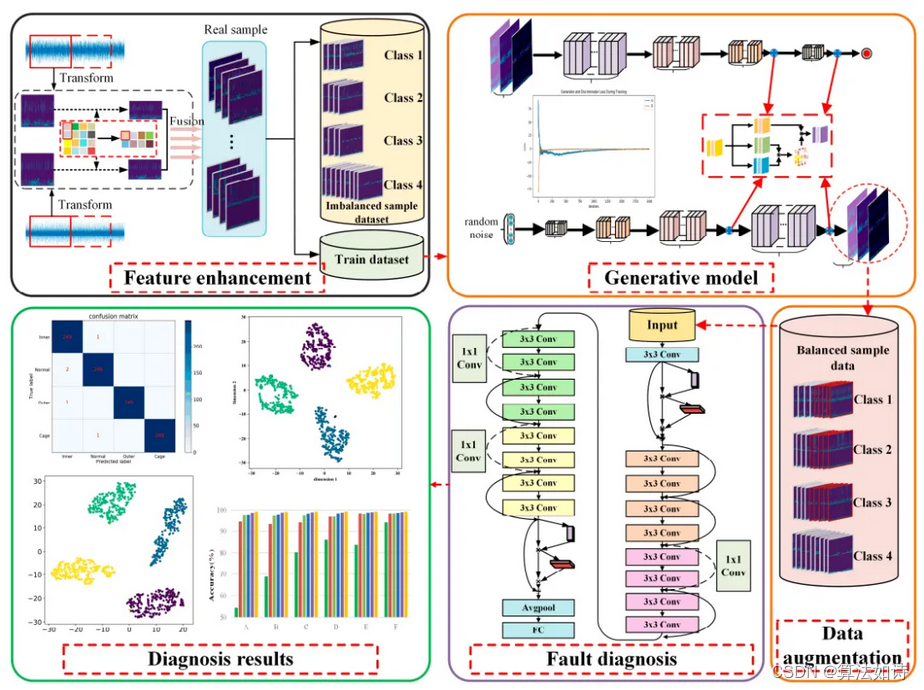
本篇为本科课程《高电压工程基础》的笔记。
液体和固体介质广泛应用于高压电气设备内,作为设备的内绝缘。描述电介质的电气特性的四大参数是介电常数 ε \varepsilon ε、电导率 γ \gamma γ、介质损耗角正切 tan δ \tan\delta tanδ和击穿场强 E b E_b Eb。对于气体绝缘介质只关心其击穿强度,而固体介质需要全部都关注。
电介质的极化、电导与损耗
电介质的极化
平行平板电容器在真空中的电容量为:
C
0
=
ε
0
A
d
C_0=\frac{\varepsilon_0 A}{d}
C0=dε0A
极板间插入固体介质之后,电容量为:
C
=
ε
A
d
C=\frac{\varepsilon A}{d}
C=dεA
所以得到介质的相对介电常数: ε r = ε ε 0 = C C 0 \varepsilon_r=\frac{\varepsilon}{\varepsilon_0}=\frac{C}{C_0} εr=ε0ε=C0C。
- 介质的极化造成了电容量的增加,外电场下介质中的正负电荷发生位移,形成了电偶极矩,介质的表面感应出了束缚电荷。
- 各种气体的 ε r \varepsilon_r εr接近于1,常见的固体和液体截止的 ε r \varepsilon_r εr大多在2~6之间。
- 各种介质的 ε r \varepsilon_r εr与温度和电源频率的关系也不相同,这和计划的形式有关。
- 计划分为电子式、离子式和偶极子式,绝缘结构中好友夹层界面极化。
- 电子式极化:原子中电子轨道受到外电场作用,相对于原子核会产生位移,原子中正负电荷中心不再重合,极化强度和正负电荷作用中心距离成正比,且随外场强增大而增大。
电子极化存在于一切介质中,所需时间极短,其 ε r \varepsilon_r εr不随频率变化。电子极化具有弹性,没有损耗。温度对他的影响不大,升温膨胀,单位体积内分子减少, ε r \varepsilon_r εr略有减小。 - 离子式极化:无外电场,正负离子作用中心重合,外电场作用下,正负离子发生位移,呈现极性。也是弹性计划,几乎无损耗, ε r \varepsilon_r εr与频率无关,而 ε r \varepsilon_r εr一般有不大的正温度系数。
- 偶极子式极化:偶极子正负电荷中心不重合,形成一个永久的偶极矩,有这样的永久偶极矩的电介质就是极性电介质。
无外电场,分子杂乱无章,整个介质不显示出极性。有外电场,各个分子顺着电场方向定向排列,显示出极性,这种计划也被称为转向极化。
偶极子式极化是非弹性的,会消耗能量,极化所需时间也长, ε r \varepsilon_r εr和电源频率有大的关系,频率很高式电偶极子来不及转动。
温度高的时候,分子热运动加剧,妨碍他们定向排列,气体的 ε r \varepsilon_r εr有负的温度系数。液体和固体温度低的时候,分子联系紧密难以转向,所以液体固体的 ε r \varepsilon_r εr低温时先随温度升高而升高,然后热运动剧烈, ε r \varepsilon_r εr又开始变小。 - 夹层介质界面极化:多层绝缘,极化过程缓慢,伴随着能量损耗。
电介质的电导
电介质的电导主要是离子电导,随温度的变化规律和与电子电导的金属材料是相反的。
液体固体介质的电导率
γ
\gamma
γ和温度
T
T
T有关系:
γ
=
A
e
−
ϕ
/
k
T
\gamma=Ae^{-\phi/kT}
γ=Ae−ϕ/kT
其中,
A
A
A是常数和介质有关,
T
T
T是热力学温度,
ϕ
\phi
ϕ是电导活化能,
k
k
k是玻尔兹曼常数。
- 固体电介质除了内部流过的电导电流 I V I_V IV外,还有沿着表面流过的表面电流 I S I_S IS。
- 电介质内部电导电流所决定的电阻就是体积电阻 R V R_V RV,电阻率是 ρ V \rho_V ρV。
- 电介质表面电导电流所决定的电阻就是表面电阻 R S R_S RS,电阻率是 ρ S \rho_S ρS。
- 液体和气体只有体积电阻。
电介质的能量损耗
一种是极化引起的损耗,一种是电导引起的损耗。
给戒指两端加上电压,流过电路的电流是包含无功(感性)和有功成分: I ˙ = I r ˙ + I c ˙ \dot{I}=\dot{I_r}+\dot{I_c} I˙=Ir˙+Ic˙,介质的损耗就是 P = Q tan δ = U 2 ω C tan δ P=Q\tan\delta=U^2\omega C\tan\delta P=Qtanδ=U2ωCtanδ。
用介质的损耗角正切 tan δ \tan\delta tanδ来判断介质的品质,它仅取决于材料的特性。
- 气体介质的损耗:当电场不足以产生碰撞电离时,主要损耗是电导产生的,损耗极小。但外加电场大于起晕电场,就会局部放电,损耗急剧增加,这被称为电晕损耗。
- 液体介质的损耗:中性或若极性液体介质损耗主要是因为电导,所以损耗很小。
极性液体介质的损耗有电导和极化两种,所以损耗很大,而且和温度与频率都有关系。- 温度低,电导和极化损耗都很小,温度升高,液体粘度减小,偶极子转向极化增强,使得损耗增加,电导损耗也随温度而上升。
- 在 T = T 1 T=T_1 T=T1时达到极大值,随后由于分子热运动加快,阻碍了规律排列,削弱了极化,极化损耗下降,整体也下降。
- 在
T
>
T
2
T>T_2
T>T2时,电导损耗随着温度升高而急剧上升,整体损耗显示出急剧上升
频率升高时,损耗曲线向右移,极大值出现在更高温。因为频率过高,电偶极子来不及转动,只有升高温度减小粘度,才能让转动进行充分。
下图就是极性液体介质 tan δ \tan\delta tanδ和温度的关系,1是频率较低的曲线,2是频率较高的曲线。

- 固体介质的损耗:中性介质损耗主要由电导引起,且这些介质电导率极其小,所以介质损耗很小。极性介质的 tan δ \tan\delta tanδ和温度、频率关系和极性液体相似。不均匀介质的损耗取决于各成分性能和数量间的比例。
液体介质的击穿
纯净的液体击穿和气体过程很相似,不过其击穿场强比气体要高得多。而工程上的液体介质中有气泡或者是杂质如水分、悬浮固体纤维等,击穿的时候再电场作用下这些气泡杂质会排列成“小桥”引起击穿。
影响液体介质击穿的因素
在极不均匀电场中,击穿前高场强去会出现局部放电,引起介质扰动,使得小桥不易形成。而均匀电场不会扰动,会形成小桥导致击穿。所以检验油的洁净程度,要使用均匀电场。
- 杂质的影响:油中的水滴会在电场的方向拉伸,极化了的水滴和杂质会向着高场强处运动,逐渐形成导电的小桥,导致液体的击穿。气泡也会影响击穿强度。
- 温度的影响:干燥油的击穿强度和温度没有什么关系,但油受潮后就和温度有很大的关系。油的击穿强度随着温度的上升而显著提升,因为水在油中的溶解度随着温度的升高而升高,当温度在高于约80°C时,由于油中的水汽化,使得击穿强度下降,但仍然比室温高。极不均匀电场中温度影响不大。
- 油体积的影响:油的击穿强度随着间隙中油的体积的增大而明显减小,因为间隙中杂质和水的出现会随着体积的增大而增多。
- 电压形式的影响:杂质形成小桥所需的时间比气体放电的时间要长,所以油间隙的冲击击穿场强比工频击穿场强要大。
减小杂质影响的措施
- 过滤:滤纸可以过滤掉纤维等固体杂质,水分等也会被滤纸吸收。
- 防潮:使用绝缘油前必须烘干,在呼吸器的空气入口防上干燥剂。
- 祛气:将油加热,喷成雾状,并抽真空。
- 用固体介质减小油中杂质的影响:常用油覆盖层、绝缘层和屏障。
固体介质的击穿
固体的固有击穿强度要比液体和气体高,击穿的影响都是永久性破坏,即固体时非自恢复绝缘。
下图是击穿场强和电压作用时间的关系。

电击穿
固体介质的电击穿和气体中类似,由碰撞电离形成电子崩,电子崩足够强时破坏介质晶格结构导致击穿。
击穿的分散性很大,与材料的不均匀性有关。加大面积或体积,使得材料弱点出现得多,使得击穿强度下降,这就是击穿体积效应。
固体介质在冲击电压多次作用下,击穿电压有可能低于一次冲击作用时的击穿电压,因为固体介质是非自恢复绝缘,每次冲击都会有损伤,这就是累计效应。有机材料有明显的累计效应。
热击穿
电场下会有电导电流和介质极化引起的损耗,使得介质发热。介质的电导率随着温度的升高而增大,因此介质发热随着温度的升高而增加。如果发热大于散热,那么就会一直提高温度到热破坏而击穿。
热击穿是一个热不平衡的过程,击穿所需的时间较长。绝缘实验中需要加长施加电压的时间。
直流电压下正常未受潮的绝缘很少发生热击穿,因为直流下没有极化损耗只有微小的电导电流。而交流随着频率的升高极化损耗也在增加。
电化学击穿
介质长期加电压会引起介质的劣化而导致击穿场强下降。
绝缘劣化主要因为介质内气隙的局部放电,工作电压下气隙的场强要大于固体介质的场强,而气隙的击穿场强又小于固体介质的击穿场强,介质中会长期存在局部放电但是不会击穿。局部放电产生的活性气体也会腐蚀介质。另外带电粒子对于介质的碰撞,也会使得其受到机械的损伤和局部过热。

如图所示为局部放电的等效电路图。其中 C g C_g Cg是空气间隙的电容, C b C_b Cb是和空气间隙串联的介质电容, C m C_m Cm是除了前两个电容外其他绝缘完好部分的电容,一般 C m ≫ C g ≫ C b C_m\gg C_g\gg C_b Cm≫Cg≫Cb。
由于电容 C g C_g Cg在较低的电压 U g U_g Ug时候就开始放电,所以等效的用放电间隙g和 C g C_g Cg并联来表示。
交流下的间隙放电
当介质两极加上瞬时值为u的交流电压时,
C
g
C_g
Cg上的电压瞬时值
u
g
u_g
ug可以根据电容分压求得:
u
g
=
u
C
b
C
g
+
C
b
u_g=u\frac{C_b}{C_g+C_b}
ug=uCg+CbCb
当 u g u_g ug达到空气间隙的放电电压 U g U_g Ug时,气隙开始击穿,相当于短路,气隙上的电压急剧下降。如图所示, C g C_g Cg上的电压达到 U g U_g Ug时电压开始急剧下降到 U r U_r Ur,才停止击穿,然后再次给 C g C_g Cg充电,当 C g C_g Cg上的电压再次达到 U g U_g Ug时开始第二次放电,直到外施加电压达到峰值, C g C_g Cg上的电压也开始改变极性,直到另一极性上的电压达到放电电压。
下图就是发生局部放电时气隙上的电压变化。

气隙击穿时的放电电荷量
现在计算气隙击穿时的放电电荷量。间隙g两端的电压变化为
U
g
−
U
r
U_g-U_r
Ug−Ur,而间隙g两端的电容量就是
C
g
+
C
m
C
b
C
m
+
C
g
C_g+\frac{C_mC_b}{C_m+C_g}
Cg+Cm+CgCmCb,所以可以得到间隙放电带你和量
Δ
q
r
\Delta q_r
Δqr,即真实放电量就是:
Δ
q
r
=
(
C
g
+
C
m
C
b
C
m
+
C
g
)
(
U
g
−
U
r
)
≈
(
C
g
+
C
b
)
(
U
g
−
U
r
)
\Delta q_r=\left( C_g+\frac{C_mC_b}{C_m+C_g}\right)(U_g-U_r)\approx(C_g+C_b)(U_g-U_r)
Δqr=(Cg+Cm+CgCmCb)(Ug−Ur)≈(Cg+Cb)(Ug−Ur)
实际中
C
g
,
C
b
,
U
g
,
U
r
C_g,C_b,U_g,U_r
Cg,Cb,Ug,Ur是无法测量的,所以真实放电量
Δ
q
r
\Delta q_r
Δqr也无法通过测量这些量计算出。
局部放电时经常使用视在放电量
Δ
q
\Delta q
Δq,根据的是放电时两级之间的电压变化
Δ
U
\Delta U
ΔU和被测试品的整体电容来确定的放电电荷量:
Δ
q
=
Δ
U
(
C
m
+
C
b
C
g
C
b
+
C
g
)
\Delta q=\Delta U\left( C_m+\frac{C_bC_g}{C_b+C_g}\right)
Δq=ΔU(Cm+Cb+CgCbCg)
电压变化 Δ U \Delta U ΔU和被测试品的整体电容都是可以测量出的,所以视在放电量 Δ q \Delta q Δq可以通过测量计算出。但是视在放电量 Δ q \Delta q Δq比起真实放电量 Δ q r \Delta q_r Δqr要小的很多。原因是:
上式可以近似的写为
Δ
q
≈
Δ
U
C
m
\Delta q\approx\Delta UC_m
Δq≈ΔUCm。可以利用分压公式写出
Δ
U
\Delta U
ΔU和
U
g
−
U
r
U_g-U_r
Ug−Ur的关系:
Δ
U
=
C
b
C
b
+
C
m
(
U
g
−
U
r
)
≈
C
b
C
m
(
U
g
−
U
r
)
\Delta U=\frac{C_b}{C_b+C_m}(U_g-U_r)\approx\frac{C_b}{C_m}(U_g-U_r)
ΔU=Cb+CmCb(Ug−Ur)≈CmCb(Ug−Ur)
带入得: Δ q = C b ( U g − U r ) \Delta q=C_b(U_g-U_r) Δq=Cb(Ug−Ur)。
把真实放电量 Δ q r \Delta q_r Δqr的式子和上式比较,得到: Δ q = C b C g + C b Δ q r \Delta q=\frac{C_b}{C_g+C_b}\Delta q_r Δq=Cg+CbCbΔqr。一般有$ C_g\gg C_b ,所以有 ,所以有 ,所以有\Delta q \ll \Delta q_r$。
局部放电的能量
利用电容储能的公式,得到放电的能量:
W
=
1
2
(
C
g
+
C
m
C
b
C
m
+
C
b
)
(
U
g
2
−
U
r
2
)
W=\frac{1}{2}\left( C_g+\frac{C_mC_b}{C_m+C_b}\right)(U_g^2-U_r^2)
W=21(Cg+Cm+CbCmCb)(Ug2−Ur2)
因为
C
m
≫
C
b
C_m \gg C_b
Cm≫Cb,所以上式可以近似写成:
W
=
1
2
(
C
g
+
C
b
)
(
U
g
+
U
r
)
(
U
g
−
U
r
)
=
1
2
Δ
q
r
(
U
g
+
U
r
)
=
1
2
Δ
q
C
g
+
C
b
C
b
(
U
g
+
U
r
)
W=\frac{1}{2}(C_g+C_b)(U_g+U_r)(U_g-U_r)=\frac{1}{2}\Delta q_r(U_g+U_r)=\frac{1}{2}\Delta q\frac{C_g+C_b}{C_b}(U_g+U_r)
W=21(Cg+Cb)(Ug+Ur)(Ug−Ur)=21Δqr(Ug+Ur)=21ΔqCbCg+Cb(Ug+Ur)
设空气间隙放电的时候,加在电介质的两外电极的电压为
U
i
U_i
Ui,可以得到
U
i
U_i
Ui和
U
g
U_g
Ug的关系:
U
g
=
U
i
C
b
C
g
+
C
b
U_g=U_i\frac{C_b}{C_g+C_b}
Ug=UiCg+CbCb
带入得: W = 1 2 Δ q U i U g ( U g + U r ) W=\frac{1}{2}\Delta q\frac{U_i}{U_g}(U_g+U_r) W=21ΔqUgUi(Ug+Ur)
直流下的局部放电
交流一个周期内会至少发生两次局部放电,且频率越高放电越频繁。而直流情况下,气隙场强大于放电场强时,虽然也有局部放电,但因此生成的正负电荷在移动到气隙壁后,就会产生和原来电场反方向的电场,使得合成电场下降,放电可能停止。直到经过气隙表面的电导的中和之后,才会开始新的放电,但这个时间比较长,达到数秒,所以危害较小。
预防措施
- 尽量消除气隙或设法减小气隙的尺寸:钢管油压电缆用高油压来消除气隙。
- 设法提高空穴的击穿场强:使用油纸绝缘。