结课大作业题目自拟：

利用蒙特卡诺法计算不规则图形的面积，由于题目自拟，所以选择用椭圆来表示待测面积的不规则图形。

代码实现：

%%先绘制一个椭圆
a=5;%长轴
b=2;%短轴
f=@(x,y) x.^2/a^2 + y.^2/b^2-1;%椭圆方程
fimplicit(f,'LineWidth',2)%绘制椭圆 
设置窗口
set(gcf,'units','normalized','position',[0.2 0.2 0.6 0.6]); %设置figure窗口位置和尺寸
grid on
axis equal
axis([-(a+0.5),(a+0.5),-(b+0.5),(b+0.5)])
pause(2)
hold on
绘制椭圆的包络矩形
rectangle('Position',[-a,-b,2*a,2*b],'EdgeColor','r','LineWidth',2)
A=4*a*b;%矩形面积
pause(2)
投放N个均匀分布的随机点
N=500;
xk=-a+(a+a)*rand(1,N);   %x坐标
yk=-b+(b+b)*rand(1,N);   %y坐标
scatter(xk,yk,'g.')
统计落在椭圆里面的随机点个数
r = xk.^2/a^2+yk.^2/b^2;
m=find(r<=1);
n=length(m);
S=(n/N)*A

效果演示：

 

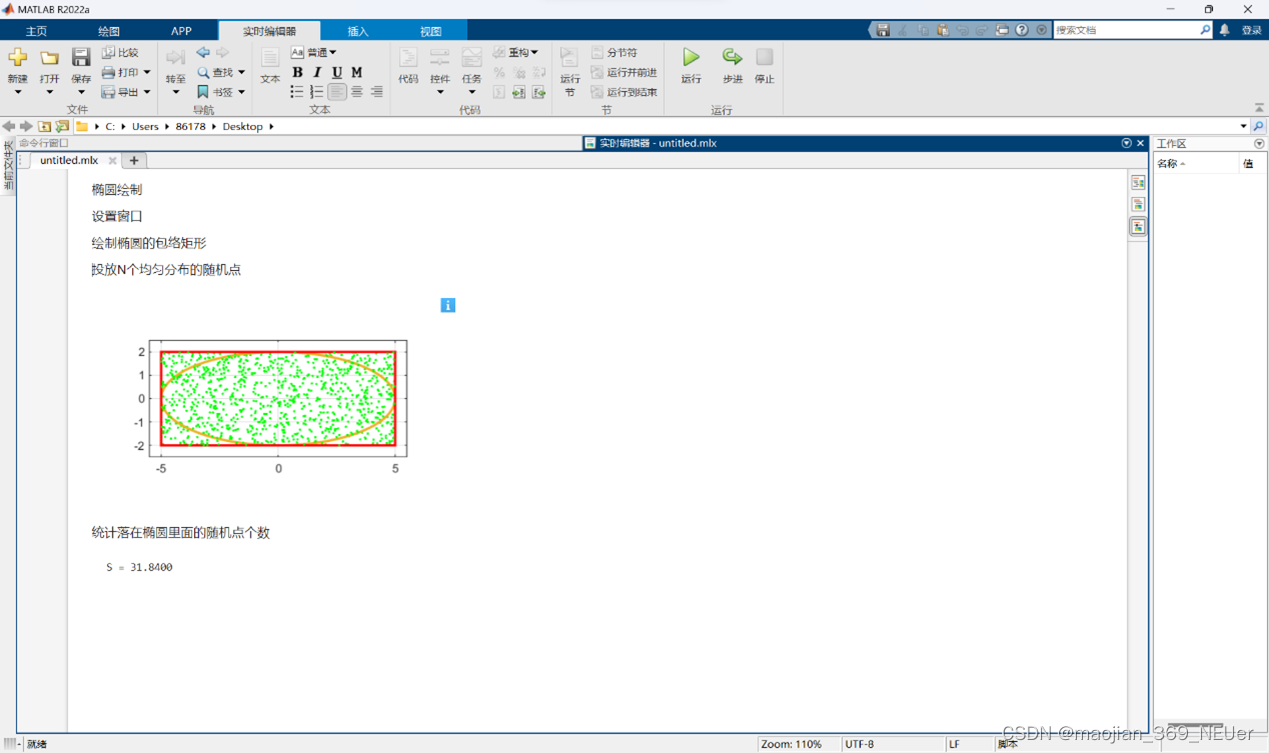
 注：由于计算过程比较复杂，所以我是选择在matlab中的实时脚本里写的。

 注：为了图像效果较好，结果图中只生成了500个随机点，结果不是很准确，增加至1000以上时，随N增大，面积值变化不再明显。

网上也有其他类似的代码，可以多方借鉴。