every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
随机游走
1. 概念
1.1 例1
在你的饮食俱乐部度过了一个富有成效的晚上后,你在不太清醒的状态下离开了。因此,你会醉醺醺地在展望大道上闲逛。首先,你可能会随机向右走一步。然后,忘记你在哪里,你可能会向左转一步。完全迷失了方向,你又随机迈出了一步…例如,对于一些步骤,您可能最终会像这样走
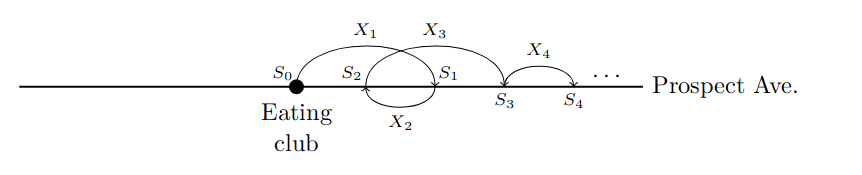
让我们把它当作一个随机过程来建模。饮食俱乐部的位置是S_0(你在零步后的初始位置)。在第k步中,移动的量为 X k X_k Xk,可以是正的,也可以是负的(取决于向左还是向右移动)。n步后的位置 S n S_n Sn由
S n = S 0 + x 1 + . . . + X n S_n = S_0+x_1+...+X_n Sn=S0+x1+...+Xn
当你喝醉的时候,你会完全忘记你每走一步都在哪里。因此,我们对步骤 X 1 X_1 X1, X 2 X_2 X2,…进行建模。为独立同分布(i.i.d)随机变量,与初始位置 S 0 S_0 S0无关。这给了我们第一个随机漫步的例子
1.2 例2
假设你和你的朋友玩下面的游戏。在每一轮中,每个玩家下注1美元,并独立地投掷一枚均匀硬币。如果硬币正面朝上,那么你赢了,也就是说,你拿回你的1美元,同时你也得到你朋友的1美元。如果硬币反面出现,那么你的朋友就赢了钱。你反复玩这个游戏,直到你们中的任何一个人决定是时候减少损失了
为了将你在游戏中的财富建模为一个随机过程,让我们假设你以50美元的初始财富开始游戏。请注意,你在每一轮的净收益是+1或1。让Xi成为你在第i轮的净收益。因为硬币是公平的,你输或赚1美元的概率是一样的
P ( X i = 1 ) = P ( X i = − 1 ) = 1 2 P(X_i =1) = P(X_i=-1) = \frac{1}{2} P(Xi=1)=P(Xi=−1)=21
我们假设, S 0 S_0 S0, X 1 X_1 X1, X 2 X_2 X2,…是独立的。因此,第n轮之后的财富 S n S_n Sn由,
S n = S 0 + x 1 + . . . + X n S_n = S_0+x_1+...+X_n Sn=S0+x1+...+Xn
一个可能的结果如下:
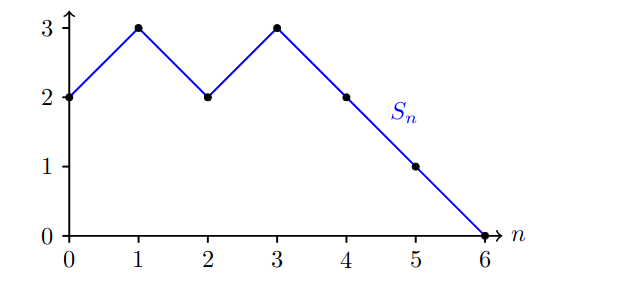
在这两个例子中,我们从起始点S0开始,制作了一系列独立同分布(i.i.d)步骤 X k X_k Xk。这样的过程被称为随机漫步。在第二个例子中,随机漫步只产生大小为1的步的情况特别重要;这叫做简单随机漫步。
1.3 定义
定义如下:
随机游走 S n , n ≥ 0 {S_n},n\geq0 Sn,n≥0为随机过程
S
n
=
S
0
+
x
1
+
.
.
.
+
X
n
S_n = S_0+x_1+...+X_n
Sn=S0+x1+...+Xn
其中,
X
1
,
X
2
,
.
.
.
X_1,X_2,...
X1,X2,...是独立同分布(i.i.d)随机变量,与
S
0
S_0
S0无关。
2. 边界
2.1 会达到边界吗?
我们必须研究的第一个问题是,随机漫步是否真的会碰到边界 { a , b } \{a, b\} {a,b},也就是说,是否 T < ∞ T< \infin T<∞ 。当然,到达边界的概率原则上可能取决于起始点S0。因此,让我们引入函数:
f ( i ) : = P ( T = ∞ , S 0 = i ) , a ≤ i ≤ b f(i) := P(T=\infin, S_0=i) , \qquad a\leq i \leq b f(i):=P(T=∞,S0=i),a≤i≤b
也就是说, f ( i ) f(i) f(i) 是我们从未碰到边界a或b中的任何一个的概率 (换句话说,随机漫步永远严格地停留在这两个边界之间),假设我们从点 S 0 = i S0 = i S0=i 开始。我们想要计算这些概率。为此,我们将引入一个非常有用的工具来研究随机漫步的行为:第一步分析(the first-step analysis)
让我们首先解释一下第一步分析背后的思想。假设我们从点 a < i < b a < i < b a<i<b严格地在边界之间开始。那么我们能到达边界的最早时间是在随机漫步的一步之后。此外,由于这是一个简单的对称随机漫步,在一步之后,我们可能到达的位置只有两个,每个位置出现的概率都是相等的:

因为随机漫步的每一步都是独立同分布的,所以随机漫步在每一步之后都会在当前位置重新开始。举个例子,如果在第一步中我们从 i → i + 1 i \rightarrow i+1 i→i+1开始,那么从这一点开始,随机漫步就像从i+1开始的随机漫步一样。特别地,第一步是 i → i + 1 i \rightarrow i + 1 i→i+1,那么之后不到达边界的概率是f (i + 1),对于其他可能的步骤也是如此
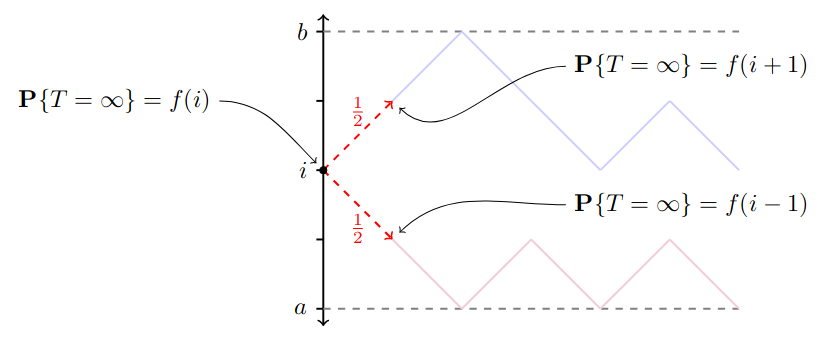
如图,我们可以得到:
f ( i ) = P ( T = ∞ ∣ S 1 = i + 1 , S 0 = i ) P ( S 1 = i + 1 ∣ S 0 = i ) + P ( T = ∞ ∣ S 1 = i − 1 , S 0 = i ) P ( S 1 = i − 1 ∣ S 0 = i ) f(i)= P(T=\infin|S_1=i+1, S_0=i)P(S_1=i+1|S_0=i)+P(T=\infin|S_1=i-1, S_0=i)P(S_1=i-1|S_0=i) f(i)=P(T=∞∣S1=i+1,S0=i)P(S1=i+1∣S0=i)+P(T=∞∣S1=i−1,S0=i)P(S1=i−1∣S0=i)
其中,
P
(
S
1
=
i
+
1
∣
S
0
=
i
)
=
1
2
P
(
S
1
=
i
−
1
∣
S
0
=
i
)
=
1
2
P(S_1=i+1|S_0=i)= \frac{1}{2} \qquad \qquad P(S_1=i-1|S_0=i)= \frac{1}{2}
P(S1=i+1∣S0=i)=21P(S1=i−1∣S0=i)=21
同时,有
P
(
T
=
∞
∣
S
1
=
i
+
1
,
S
0
=
i
)
=
f
(
i
+
1
)
P
(
T
=
∞
∣
S
1
=
i
−
1
,
S
0
=
i
)
=
f
(
i
−
1
)
\begin{align} P(T=\infin|S_1=i+1, S_0=i)=f(i+1) \\ P(T=\infin|S_1=i-1, S_0=i)=f(i-1) \end{align}
P(T=∞∣S1=i+1,S0=i)=f(i+1)P(T=∞∣S1=i−1,S0=i)=f(i−1)
因此,
f ( i ) = 1 2 f ( i + 1 ) + 1 2 f ( i − 1 ) , a < i < b f(i)= \frac{1}{2}f(i+1)+\frac{1}{2}f(i-1),\qquad a < i < b f(i)=21f(i+1)+21f(i−1),a<i<b
另一方面,假设我们从S0 = a或S0 = b开始,那么我们一开始就已经从边界开始了,所以我们从未到达边界的概率为零。特别地,这意味着f (a) = f (b) = 0。因此,我们的第一步分析使我们得到以下等式
{ f ( i ) = 1 2 f ( i + 1 ) + 1 2 f ( i − 1 ) , a < i < b f ( a ) = f ( b ) = 0 \begin{cases} f(i)= \frac{1}{2}f(i+1)+\frac{1}{2}f(i-1),\qquad a < i < b \\ f(a)=f(b)=0 \end{cases} {f(i)=21f(i+1)+21f(i−1),a<i<bf(a)=f(b)=0
通过变换方程我们知道,f(i)位于f(i-1)和f(i+1)中间位置。同时,在一条直线上。
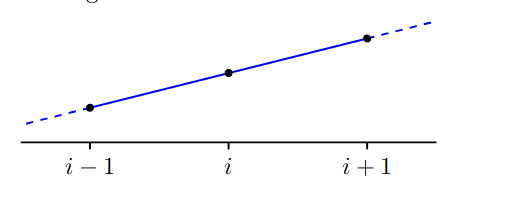
所以,f(i)是直线。又,f(a)=f(b)=0,可得f(i)=0:
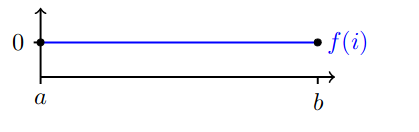
P ( T = ∞ ∣ S 0 = i ) = 0 , f o r a l l a ≤ i ≤ b P(T=\infin|S_0=i)=0, \qquad for all a \leq i \leq b P(T=∞∣S0=i)=0,foralla≤i≤b
所以,随机漫步最终总是到达a或b,而不管它的起点是什么。
2.2 会达到哪一个边界
既然我们知道我们最终总会碰到边界a或b中的一个,我们可能想知道我们先碰到哪一个?例如,在赌博问题中, T < ∞ T <\infin T<∞表示你最终要么赢得100美元要么破产。在实践中,您可能对这些结果中哪一种更有可能发生非常感兴趣。
为了深入了解这个问题,让我们用数学术语来表达它。在我们到达a或b的第一时间T,值 S T S_T ST显然必须是a或b。我们感兴趣的是计算 S T = b S_T = b ST=b的概率,比如(在这种情况下,随机行走在到达a之前到达b)。由于这个概率可能再次取决于我们开始随机行走的位置,让我们定义这个函数
r ( i ) : = P ( S T = b ∣ S 0 = i ) r(i) := P(S_T=b|S_0 = i) r(i):=P(ST=b∣S0=i)
为了计算r(i),我们可以再次使用第一步分析。如果a < i < b,那么一步之后我们可以最早到达其中一个边界。一步之后,我们在i + 1或i -1处的概率相等,在a之前到达b的概率分别由r(i + 1)和r(i - 1)给出。正如上文所述,我们因此发现
r ( i ) = 1 2 r ( i + 1 ) + 1 2 r ( i − 1 ) , a < i < b r(i) = \frac{1}{2}r(i+1)+\frac{1}{2}r(i-1), \qquad a < i < b r(i)=21r(i+1)+21r(i−1),a<i<b
这里不同的是边界条件。在这种情况下,如果我们从S0 = b开始,那么我们显然会在a之前到达b(因为我们已经从b开始了!),所以r(b) = 1。另一方面,如果S0 = a,那么显然a在b之前,所以r(b) = 0。因此,我们得到以下线性方程
{ r ( i ) = 1 2 r ( i + 1 ) + 1 2 r ( i − 1 ) , a < i < b f ( a ) = 0 , f ( b ) = 1 \begin{cases} r(i)= \frac{1}{2}r(i+1)+\frac{1}{2}r(i-1),\qquad a < i < b \\ f(a)=0, \quad f(b)=1 \end{cases} {r(i)=21r(i+1)+21r(i−1),a<i<bf(a)=0,f(b)=1
同样,我们可以通过变换方程将r(i)表示为一条直线。同时r(a)=0,r(b)=1,如下:
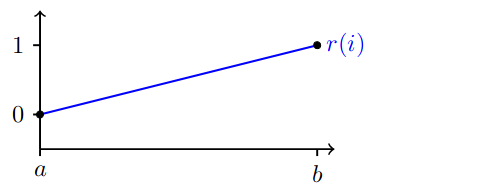
最终公式如下:
P ( S T = b ∣ S 0 = i ) = r ( i ) = i − a b − a , a ≤ i ≤ b P(S_T=b|S_0=i)= r(i) = \frac{i-a}{b-a}, \qquad a \leq i \leq b P(ST=b∣S0=i)=r(i)=b−ai−a,a≤i≤b
我们越接近b,我们越有可能在a之前碰到b,而我们越接近a,我们越有可能在b之前碰到a,这和直觉上一致。
上面的赌博游戏,直到你破产或达到100美元的财富。让它成为游戏结束的时间。我们已经证明了 T < ∞ T <\infin T<∞(游戏最终结束),你获得100美元的概率是:
P ( S T = 100 ∣ S 0 = i ) = i 100 , 0 ≤ i ≤ 100 P(S_T=100|S_0=i) = \frac{i}{100}, \quad 0 \leq i \leq 100 P(ST=100∣S0=i)=100i,0≤i≤100
即,如果你开始有i美元,你最终有100美元的概率是i/100。
让我们计算一下期望,
E ( S T ∣ S 0 = i ) = 0 ∗ P ( S T = 0 ∣ S 0 = i ) + 100 ∗ P ( S T = 100 ∣ S 0 = i ) = i E(S_T|S_0=i) = 0*P(S_T=0|S_0=i)+100*P(S_T=100|S_0=i) = i E(ST∣S0=i)=0∗P(ST=0∣S0=i)+100∗P(ST=100∣S0=i)=i
最终,你的拥有的钱和初始状态一样。