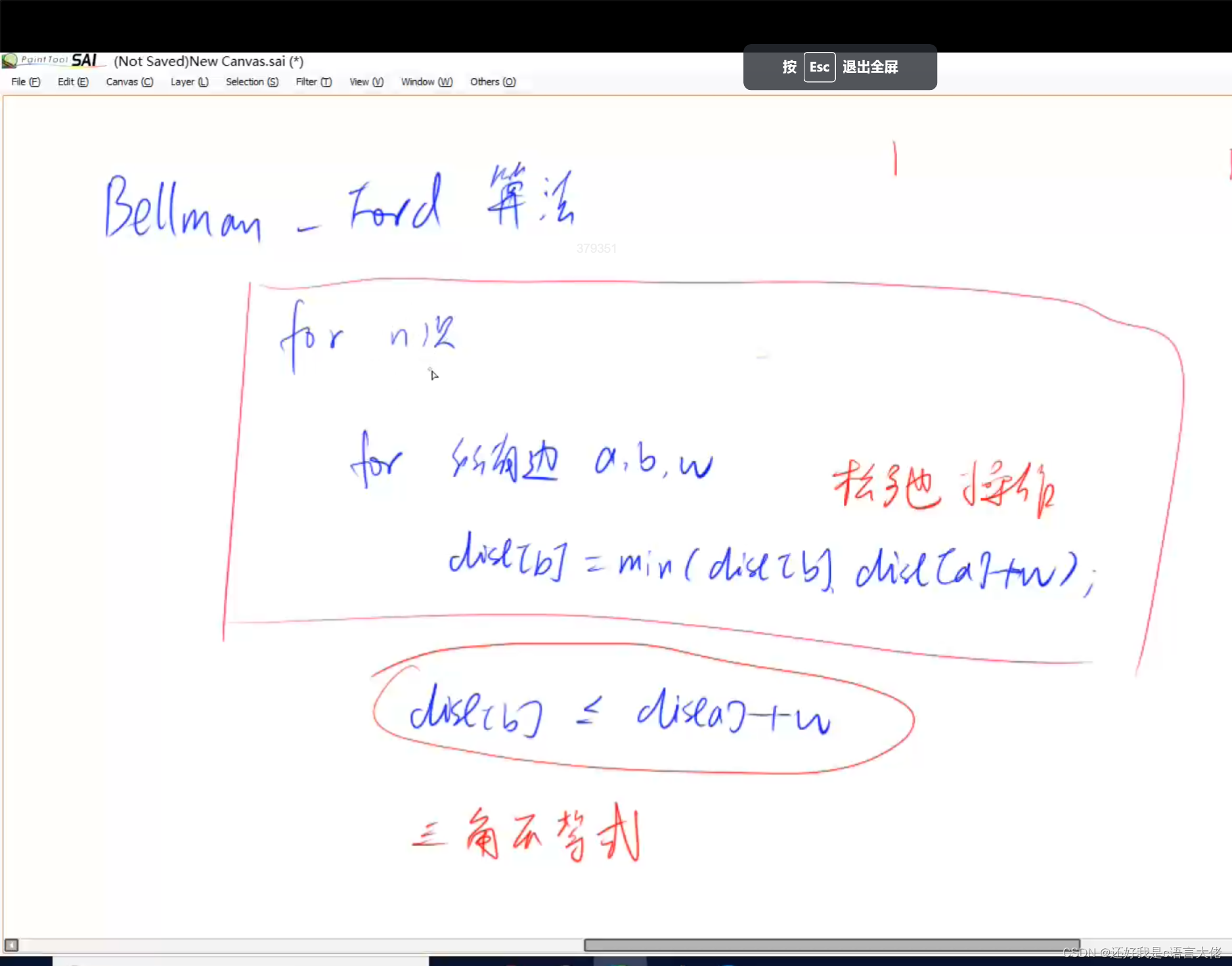
bellman-ford算法 时间复杂度O(nm)
在一般情况下,spfa算法都优于bf算法,但遇到最短路的边数有限制的题时,只能用bf算法
bf算法和dijkstra很像
#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510,M = 10010;
int n,m,k;
int dist[N],backup[N]; //backup备份数组
struct Edge{
int a,b,w;
}Edge[M]; //存所有边
int bellman_ford(){
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
for(int i = 0;i < k;i ++ ){
memcpy(backup,dist,sizeof dist); //备份dist,不会出现串联情况
for(int j = 0;j < m;j ++ ){
int a = Edge[j].a,b = Edge[j].b,w = Edge[j].w;
dist[b] = min(dist[b],backup[a] + w);
}
}
if(dist[n] > 0x3f3f3f3f / 2) return 0;
else return dist[n];
}
int main(){
cin >> n >> m >> k;
for(int i = 0;i < m;i ++ ){
int a,b,w;
cin >> a >> b >> w;
Edge[i] = {a,b,w};
}
int t = bellman_ford();
if(!t) cout << "impossible" << endl;
else cout << t << endl;
return 0;
}spfa算法 时间复杂度一般O(m), 最坏O(nm)
基本上单源最短路都可以用spfa来解决
spfa的核心优化思路是:拿我更新过的点来更新别人。一个点如果没有被更新过的话,拿它来更新别人一定是没有效果的,只有该点变小了,该点后面的点才会变小
spfa代码和堆优化dijkstra特别像
spfa算法求最短路
#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N = 150010;
int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];
bool vis[N];
int add(int a,int b,int c){
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx,idx ++ ;
}
int spfa(){
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
queue<int> q; //队列里存的是变小的a
q.push(1);
vis[1] = true;
while(q.size()){
int t = q.front();
q.pop();
vis[t] = false;
for(int i = h[t];i != -1;i = ne[i]){
int j = e[i];
if(dist[j] > dist[t] + w[i]){
dist[j] = dist[t] + w[i];
if(!vis[j]){
q.push(j);
vis[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return 0;
return dist[n];
}
int main(){
cin >> n >> m;
memset(h,-1,sizeof h);
while(m -- ){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
}
int t = spfa();
if(!t) cout << "impossible" << endl;
else cout << t << endl;
return 0;
}
spfa算法求负环
spfa算法可以求出负环用的是抽屉原理,即把多于n+1个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。
代码在spfa求最短路的模板上稍加改动即可
#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N = 150010;
int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N],cnt[N];
bool vis[N];
int add(int a,int b,int c){
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx,idx ++ ;
}
bool spfa(){
queue<int> q;
for(int i = 1;i <= n;i ++ ){ //由于存在的负环1号点可能走不到,所以要把每一个点都推进队列
vis[i] = true;
q.push(i);
}
vis[1] = true;
while(q.size()){
int t = q.front();
q.pop();
vis[t] = false;
for(int i = h[t];i != -1;i = ne[i]){
int j = e[i];
if(dist[j] > dist[t] + w[i]){
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1; //最重要的一步,如果j被更新了最短路,那么意味着j点的cnt是前一个点t+1条边达到的
if(cnt[j] >= n) return true;
if(!vis[j]){
q.push(j);
vis[j] = true;
}
}
}
}
return false;
}
int main(){
cin >> n >> m;
memset(h,-1,sizeof h);
while(m -- ){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
}
if(spfa()) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}