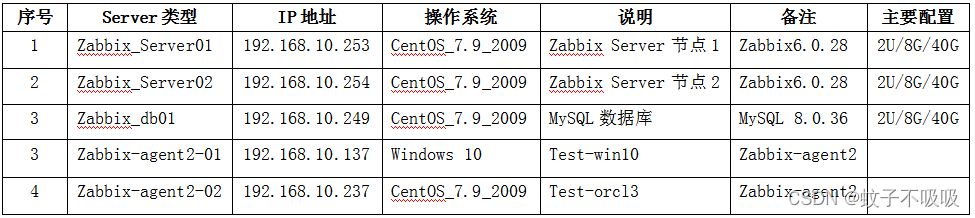
文章目录
- 11.左叶子之和
- 11.1问题
- 11.2解法一:递归
- 11.2.1递归思路
- 11.2.2代码实现
- 11.3解法二:栈
- 11.3.1栈思想
- 11.3.2代码实现
- 12.找树左下角的值
- 12.1问题
- 12.2解法一:层序遍历
11.左叶子之和
11.1问题
给定二叉树的根节点 root ,返回所有左叶子之和。
- 示例一:
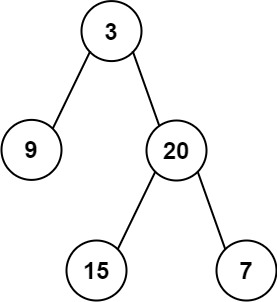
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
11.2解法一:递归
- 题目要求求左叶子之和,那什么是左叶子呢?
- 左叶子即:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
- 因此我们需要根据孩子的父节点来判断,该孩子是否为左叶子节点
11.2.1递归思路
- 递归遍历以root为根节点的树,求其左叶子之和
public int sumOfLeftLeaves(TreeNode root)
- 结束条件:
if(root==null){
return 0;
}
//也可以不用加下面这段代码
//若为叶子节点则不用递归了,因为我们根据父节点来进行递归
if(root.left==null && root.right==null){
return 0
}
- 递归逻辑
- 递归求左节点的左叶子之和
- 若该节点的左孩子为左叶子,即找到了以该节点为根节点的左叶子之和
- 递归求右节点的左叶子之和
- 递归求左节点的左叶子之和
int leftValue=sumOfLeftLeaves(root.left);
if(root.left!=null && root.left.left==null && root.left.right==null){
leftValue=root.left.val;
}
int rightValue=sumOfLeftLeaves(root.right);
int sum = leftValue+rightValue;
return sum;
11.2.2代码实现
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
//递归
if(root==null){
return 0;
}
int leftValue=sumOfLeftLeaves(root.left);
if(root.left!=null && root.left.left==null && root.left.right==null){
leftValue=root.left.val;
}
int rightValue=sumOfLeftLeaves(root.right);
int sum = leftValue+rightValue;
return sum;
}
}
11.3解法二:栈
11.3.1栈思想
- 使用栈模拟实现递归
- 思想为中左右/中右左
11.3.2代码实现
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
//栈
Stack<TreeNode> stack=new Stack<>();
int sum=0;
if(root==null){
return sum;
}
stack.push(root);
while(!stack.isEmpty()){
TreeNode node=stack.pop();
if(node.left!=null && node.left.left==null && node.left.right==null){
//该node节点的左孩子为左叶子
sum+=node.left.val;
}
if(node.left!=null){
stack.push(node.left);
}
if(node.right!=null){
stack.push(node.right);
}
}
return sum;
}
}
12.找树左下角的值
12.1问题
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
- 示例一:
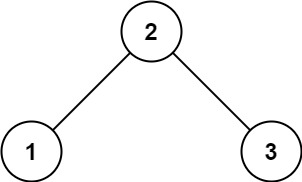
输入: root = [2,1,3]
输出: 1
12.2解法一:层序遍历
- 只需在每层遍历的时候,标记最左边的元素即可
- 注意,节点的左右孩子的放入队列顺序:左孩子先(先进先出)
class Solution {
public int findBottomLeftValue(TreeNode root) {
//层序遍历
int leftValue=0;
if(root==null){
return 0;
}
Queue<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int size=queue.size();
for(int i=0;i<size;i++){
TreeNode node=queue.poll();
if(i==0){
//每一层的最左边
leftValue=node.val;
}
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
}
return leftValue;
}
}