源自：航空尖兵

作者：康冰冰  姜涛 曹建  魏晓晴 

“人工智能技术与咨询”  发布

摘 要

针对以特定角度攻击面目标的制导律设计问题,采用深度确定性策略梯度算法构建强化学习制导律模型,设计了模型状态、奖励规则及制导环境。通过设定不同的初始条件和攻击角度,训练强化学习制导律模型,获得了稳定的制导律。强化学习制导律能够使导弹以设定的落角命中固定目标,以较小的落角误差命中低速运动面目标。仿真结果表明,与带落角约束的最优制导律相比,带落角约束的强化学习制导律的约束角度收敛速度更快,加速度变化更加平滑,制导末时刻的加速度值更小,适应战场环境的能力更强。

关键词

制导律, 强化学习, 深度确定性策略梯度, 落角约束, 马尔可夫, 智能算法

引 言

毁伤目标首先考虑的因素是武器弹药能否命中目标或者脱靶量是否在一定的毁伤范围内。与非制导武器相比, 制导武器极大的提高了命中目标的精度, 保证了毁伤效果。制导律是制导武器提高命中精度的核心之一, 制导律一般通过最优控制、 李雅普诺夫稳定性理论、 滑模控制等算法[1]设计, 最常用的制导律是比例导引律及其偏置形式[2]。

在实际作战中, 弹目交会情形和目标易损特性等也极大的影响作战使用效率, 如攻击混凝土结构、 钢制结构等坚硬目标时, 弹着角过小容易发生跳弹; 攻击舰船、 建筑物等目标时, 导弹以一定的方向攻击目标的易损部位, 可以增加毁伤效果。因此, 针对特定目标, 尤其是地面、 海面目标, 制导武器以一定的角度攻击目标, 可以达到更好毁伤效果。

针对固定目标, 文献[3]利用计算几何学设计了制导律, 调整终点碰撞线, 导弹能以指定落角攻击目标, 通过调整轨迹长度控制导弹飞行时间; 文献[4]利用直线飞行的虚拟领弹建立几何关系, 采用最优控制使跟踪弹飞行轨迹与虚拟领弹同步, 实现了特定落角攻击目标; 文献[5]利用最优控制推导带落角约束的偏置比例制导律; 文献[6]推导了三维协同制导律, 制导过程分为协同、 比例导引两个阶段, 基于此研究了导弹以不同的落角攻击目标的协同制导律[7]; 文献[8]利用李雅普诺夫稳定性定理, 设计制导误差并进行收敛设计, 实现了具有固定落角的协同制导; 文献[9]以比例制导律为基础设计了具有固定落角约束的制导律, 且收敛时间固定。

针对具有约束的制导问题, 传统的设计方法一般计算比较复杂, 有的还需要做一些近似处理。近年来, 随着人工智能的发展, 智能算法开始进入武器领域, 文献[10]综述了智能航迹规划算法, 对强化学习、 神经网络、 深度学习等算法进行了分析; 文献[11]利用深度神经网络预测导弹撞击目标的时间, 实现导弹协同攻击固定目标; 文献[12]针对机动目标采用DDPG设计了制导律, 与比例制导律、 改进的比例制导律相比, 脱靶量更小, 拦截效果更好; 文献[13]采用Q-learning、 EBDQN设计了导航比具有自适应特性的末制导律, 与传统方法相比, 脱靶量更小, 更加稳定; 文献[14]设计了DQN与神经网络结合的制导律, 与DQN制导律相比, 脱靶量更小; 文献[15]设计了基于TD3算法的制导律, 制导律的泛化特性较好; 文献[16]设计了基于TRPO的强化学习制导律, 与比例制导律相比, 具有更好的拦截效果; 文献[17]设计了基于蒙特卡洛和Q-learning的两种强化学习的导航比, 与传统比例制导律相比, 具有更好的拦截效果; 文献[18]基于分层强化学习算法研究了空战决策, 结果表明训练的模型能有效提高辅助决策效率; 文献[19]利用DDPG算法构建了制导、 控制一体化框架, 算法直接输出舵偏量, 该算法的能耗更低。

比例制导律及其变型是应用广泛的制导律, 当弹目交会状态有一定约束时, 尤其是目标存在一定的速度时, 传统制导律能否适应复杂的战场环境值得分析。由于强化学习在制导律设计上展现出了独特的优势, 受此启发, 本文采用强化学习算法, 针对具有落角约束的制导问题展开研究, 并与传统的最优制导律(扩展比例制导律)对比分析, 验证了强化学习制导律的有效性和对战场环境的适应性。

1 问题描述

如图1所示, 采用二维平面图描述空面导弹攻击固定目标的情形, 导弹简化为平面上的一个点, 并假定导弹速度恒定, 加速度只能改变速度的方向。图中, T为要攻击的固定目标, 坐标在原点为(0,0); 空面导弹M末制导初始时刻位于(xM, yM); 速度是恒定值为vM; 加速度为aM; LOS为弹目视线; l为弹目距离; η为弹道倾角; θ为弹目视线角; θF为终端落角; ζ为方向误差角。由于末制导导引头需要对目标进行探测, 因此, 假定方向误差角

。

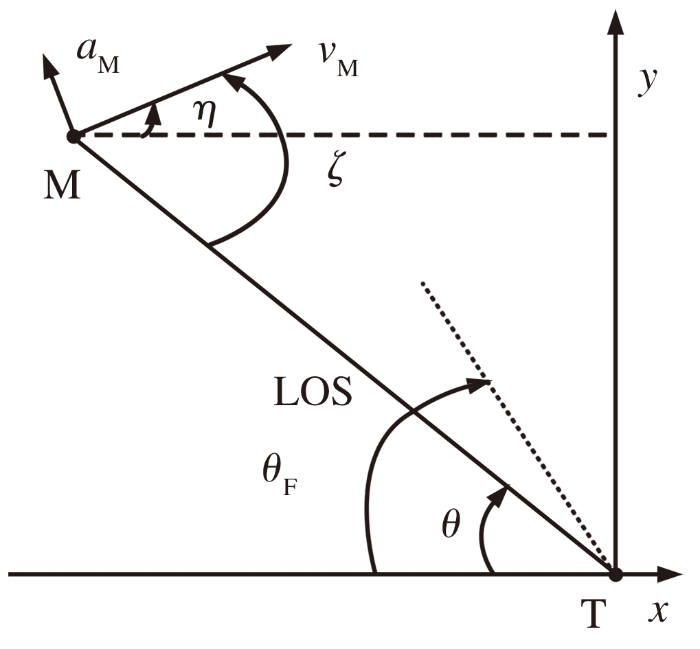
图1   弹目几何关系

弹目几何关系可以用下式表示:

(1)

(2)

(3)

(4)

整理式(2)~(4)得

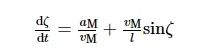
(5)

2 最优制导律

最优制导律(Optimal Guidance Law, OPL)是传统成熟的制导律, 设初始弹目距离l=l0, 终端弹目交会时弹目距离接近0, 令lF=0, 终端落角约束为θF。

在以上约束条件下, 性能指标函数设定为

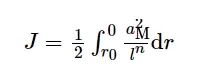
(6)

式中:n≥0。

根据最优制导律的求解方法得到加速度[2]:

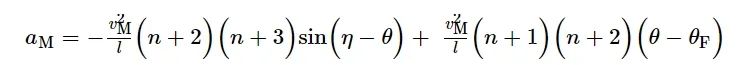
(7)

式(7)是扩展比例制导律的形式, 考虑到空面导弹的过载限制, 本文令加速度满足-90≤aM≤90。

3 强化学习制导律

3.1 强化学习

在机器学习中, 各种学习算法通常需要批量的输入数据和对应的输出数据或标签数据, 这些数据集还应满足独立同分布。通过对数据的训练, 机器学习寻得数据的内在规律, 训练好的模型可以对一个输入数据进行输出预测, 并且预测值与观测值一致或预测误差很小。但是在一些情况下, 数据是序列的, 不满足独立同分布。例如导弹制导问题, 前一时刻与后一时刻的制导飞行数据间有强相关关系, 需要连续的制导飞行数据才能确定制导律的好坏, 一个特定时刻的加速度值无法做出正确的判断。这就是强化学习要解决的问题。

强化学习基本原理如图2所示, 智能体是做出决策的机器, 智能体感知环境状态st计算出相应决策动作at, 动作at作用于环境产生了奖励r, 环境进入下一个状态st+1, 智能体根据新的状态做下一个决策。依照一定的算法, 可以计算出使累计奖励最大的决策动作序列, 这就是强化学习的思想。

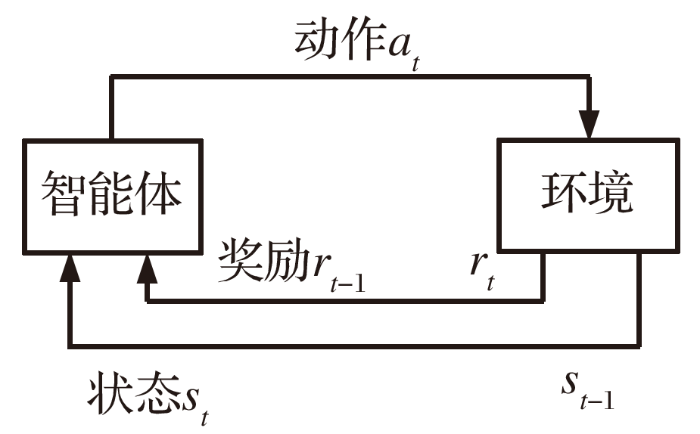
图2   强化学习

强化学习的核心是马尔科夫决策过程, 马尔科夫决策过程可由一个五元组[S, A, P, r, γ]表示。S为由状态构成的集合, 状态可以是离散的, 也可以是连续的; A为由动作构成的集合, 动作集合可以是有限的, 也可以是无限的; r为奖励函数, 通常表示为r(s,a), r的值由状态s及动作a共同确定, 考虑到动作a影响状态s, 在某些情况下r也可表示为r(s); P(s'|s,a)为状态转移的概率函数, 即在状态s下采取动作a进入下一个状态s'的概率; γ为折扣参数, 通常是介于0到1之间的数。

为了判断智能体决策的优劣, 将t时刻以后的奖励相加得到Gt, 并称为回报:

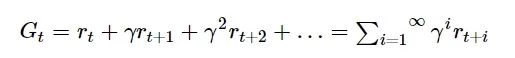
(8)

考虑到马尔科夫决策过程可能处于无限循环,折扣参数γ<1可以避免回报无限的大。rt 是现时刻得到的奖励值,而t+1时刻以后的奖励r(t+i)是对未来的估计值,存在一定的不确定性。降低折扣参数可以提高现时刻奖励的重要程度,同时降低未来时刻的不确定性。

这样智能体以最大化回报的期望为目标,以当前状态为输入,输出一个动作。智能体选择动作的规则或者函数称为策略π,可表示为

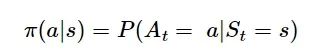
(9)

式中:P为概率函数,表示智能体根据输入状态s输出动作a的概率。如果P是在输入状态s输出动作集A的概率分布,则这个策略是随机性策略,策略根据概率采样输出一个动作a; 如果在输入状态s下输出一个确定的动作,即输出该动作的概率,P=1,则这个策略就是确定性策略。

判断策略的好坏是通过贝尔曼期望方程实现的:

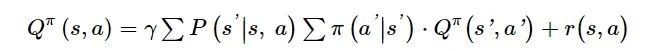
(10)

(11)

式中: Qπ(s,a)为策略π下的动作价值函数; Vπ(s)为策略π下的状态价值函数。

3.2 深度确定性策略梯度(DDPG)算法

DDPG算法是可以处理连续动作空间的离线学习策略。DDPG算法框架如图3所示, 策略网络和评价网络均使用神经网络结构。策略网络用于拟合状态s与动作a的函数关系a(s), 策略网络在动作价值的评判下, 通过训练寻找最优策略。估计网络用来拟合状态s、 动作a与奖励r的函数关系r(s,a), 通过离线的数据进行训练。策略网络、 评价网络和环境构成了一个完整的马尔可夫决策过程。估计策略网络和目标策略网络具有相同的神经网络结构, 神经网络参数分别为σ和σ'。估计评价网络和目标评价网络具有相同的神经网络结构, 神经网络参数分别为ω和ω'。采用两套相同评价网络和策略网络是为了防止神经网络参数变化过于剧烈, 解决神经网络训练不稳定的问题。估计网络实时更新参数ω和σ, 目标网络按照下式软更新参数ω'和σ':

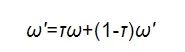
(12)

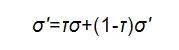
(13)

式中: 0<τ≤1。

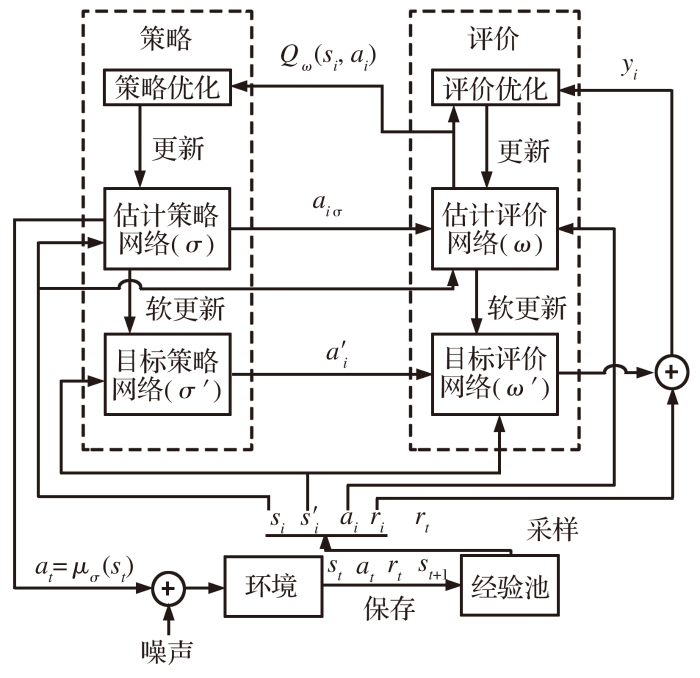
图3   DDPG算法

估计评价网络按照下式, 最小化目标损失更新网络参数ω:

(14)

式中: Qw(si,ai)为估计评价网络的输出; yi为目标评价网络的输出, 

为目标策略网络输出。

估计策略网络采用链式法则最大化Qw梯度策略更新估计策略网络参数σ:

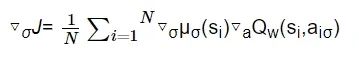
(15)

式中: ai=μσ(si)。

DDPG算法具体流程如下:

• (1) 用随机参数初始化估计策略网络和评价网络;

• (2) 复制估计网络参数至目标网络并初始化;

• (3) 随机初始状态s1和噪声, 利用估计网络循环计算并与环境交互, 保存得到的st, at, rt, st+1至经验池;

• (4) 获得足够的样本后, 采样N个数据组si, ai, ri, si+1;

• (5) 采用式(14)最小化目标函数L, 并更新估计策略网络的参数σ;

• (6) 采用式(15), 通过梯度上升方法最大化Qw, 并更新估计评价网络的参数ω;

• (7) 采用式(12)~(13)软更新目标策略网络参数σ'和目标评价网络参数ω';

• (8) 用更新后的估计网络继续采样、 保存, 重复步骤4~7。训练过程中, 按照一定的规则逐渐降低噪声直至为0。

3.3 制导律训练模型

DDPG算法能否收敛与状态量的选择、 奖励的设计息息相关。状态s参照式(7)选择为θ, 

。为了使空面导弹击中目标, 并且保证弹目视线角θ 收敛到 θF, 奖励r设计为

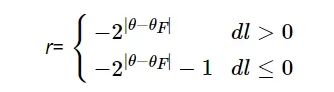
(16)

以上奖励函数的目的是将弹目视线角θ收敛到θF, 并使导弹沿弹目视线(弹目视线θF)飞行。此时, 导弹可能飞向目标, 也可能远离目标, 因此当导弹远离目标时进行惩罚。只要能保证导弹沿弹目视线角为θF的弹目视线飞向目标, 导弹能够命中目标。

式(1)~(4)构成环境, 在初始条件下DDPG算法与环境交互。

动作a是加速度, 考虑空面导弹的过载限制, 令动作满足-90≤a≤90。

为了保证训练模型的泛化能力, 末制导初始时刻导弹M在服从中心为(-5 000 m, 5 000 m), 方差为500的正态分布的随机位置; 导弹速度vM=300 m/s; 终端落角θF为服从均匀分布[-1.4,-0.3]的随机位置; 弹道倾角η为服从以0为中心, 方差为0.2的正态分布的随机位置。在不同初始条件下对模型训练, 得到稳定的强化学习制导律。

4 仿真分析

为分析强化学习制导律的特性, 设置3种不同初始条件进行分析, 如图4~8所示。

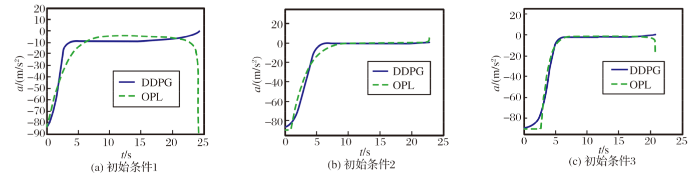
图4   加速度变化情况

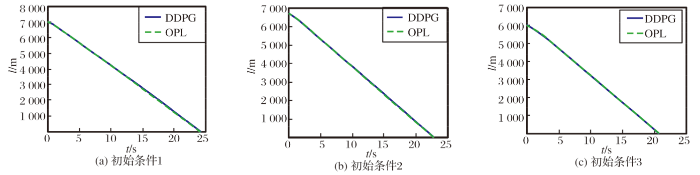
图5   弹目距离变化情况

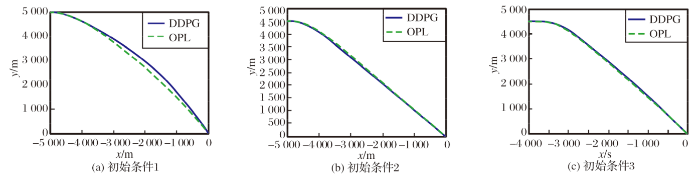
图6   导弹位置变化情况

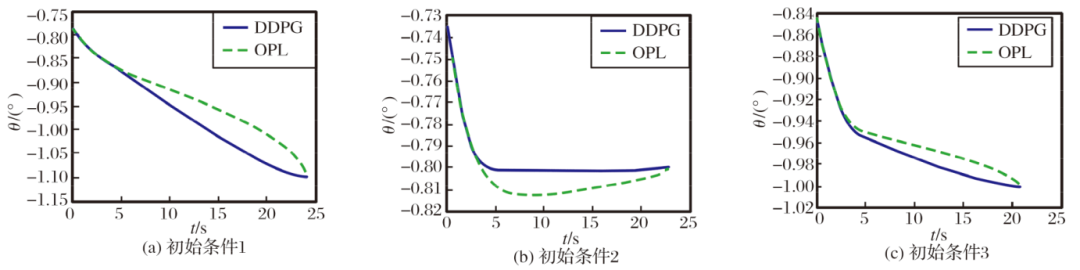
图7   弹目视线角变化情况

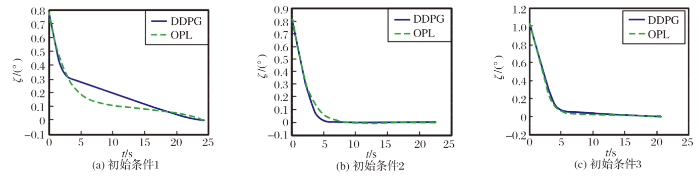
图8   导弹方向误差角变化情况

初始条件1: 导弹位置(-5 000 m, 5 000 m), 终端落角为-1.1, 弹道倾为0, 最优制导律式(7)中n=1。

初始条件2: 导弹位置(-5 000 m, 4 500 m), 终端落角为-0.8, 弹道倾为0.1, 最优制导律式(7)中n=0。

初始条件3: 导弹位置(-4 000 m, 4 500 m), 终端落角为-1.0, 弹道倾为0.2, 最优制导律式(7)中n=2。

从图中可以看出, 在3种不同初始条件下, 强化学习制导律均能以期望的落角命中目标, 且加速度在允许范围内, 弹道平滑。本文训练的模型泛化能力较好, 能够满足制导要求。

通过对比可以发现: 最优制导律在末制导初始时刻加速度值较大, 尤其是图4(c)中以最大过载飞行时间较长; 在制导末时刻加速度的绝对值会有一个增大, 尤其是图4(a)中加速度的绝对值急剧增加。强化学习制导律在末制导初始时刻所需的加速度较小, 在制导末时刻加速度接近0, 加速度变化比较平缓。从图7中可以看出, 与最优制导律相比, 强化学习制导律收敛到固定攻击角度的速度更快。从图8中可以看出, 与最优制导律相比, 强化学习制导律能够使速度更快的指向LOS方向。

为分析目标为低速面目标时的制导律特性, 令动目标匀速直线运动, 以目标速度为15 m/s, 速度方向服从均匀分布[-π,π]为条件, 在训练好的固定目标强化学习制导律的基础上继续进行训练, 得到了稳定的强化学习制导律。

设定初始条件4: 导弹位置(-5 000 m,5 000 m), 终端落角为-1.0, 弹道倾为0.2, 目标速度方向为1, 最优制导律式(7)中n=2。

强化学习制导律和最优制导律均能命中目标, 如图9所示。运动的目标使弹目视线一直在变化, 这致使制导律需要不断的调整导弹的飞行方向, 修正制导误差有一定的滞后性。从仿真结果图9(c)中可以看出, 最优制导律的终端落角为-0.92, 终端落角的误差为0.08; 强化学习制导律的终端落角为-0.97, 终端落角的误差为0.03。强化学习制导律在应对运动目标的多约束制导问题上具有更好的效果, 能更好适应变化的战场环境。

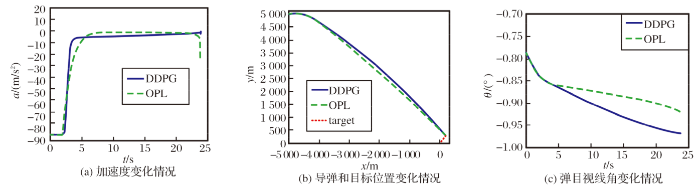
图9   初始条件4

5 结论

针对空面导弹以一定的落角攻击面目标的问题, 本文采用DDPG算法进行了制导律设计并进行训练。DDPG制导律仿真结果表明: 模型的泛化能力较好, 能以期望的落角命中目标, 且加速度在允许范围内, 弹道平滑, 在不同初始条件下均能够满足制导要求。DDPG制导律比最优制导律有更快的收敛速度、 更好的加速度特性。针对低速移动目标, DDPG制导律的终端落角误差比最优制导律小, 能更好的适应制导过程中的变化的战场环境。

声明:公众号转载的文章及图片出于非商业性的教育和科研目的供大家参考和探讨，并不意味着支持其观点或证实其内容的真实性。版权归原作者所有，如转载稿涉及版权等问题，请立即联系我们删除。

“人工智能技术与咨询”  发布