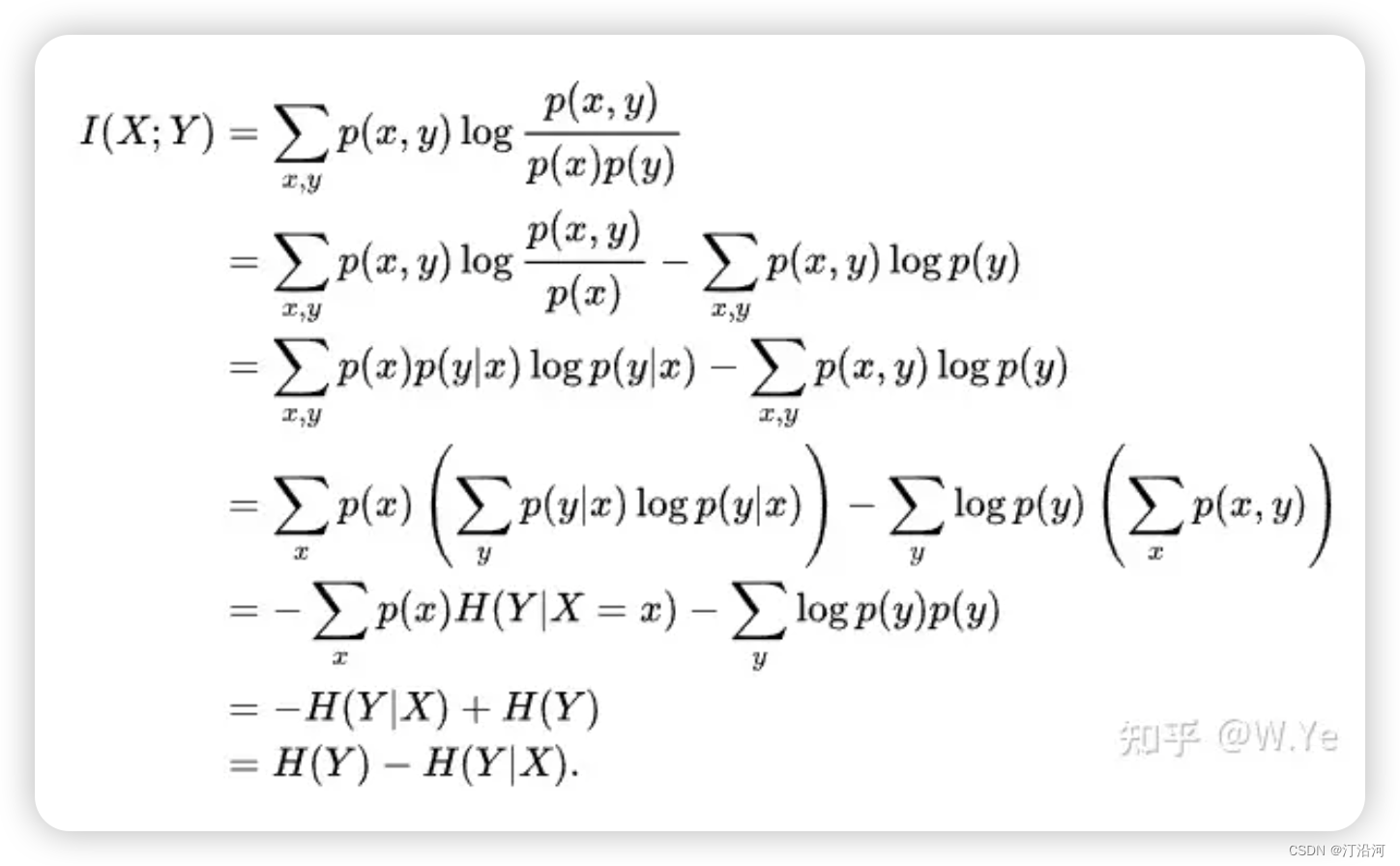文章目录
- 一、计算机中的数据存储
- 二、十进制
- 1、十进制加法
- 2、十进制减法
- 三、什么是二进制?
- 二进制的运算过程
- 四、常见的进制
- 五、计算机为什么要用二进制存储数据?
- 六、进制之间的转换
- 1、任意进制转十进制
- 1)二进制101转十进制
- 8421快速转换法
- 2)八进制101转十进制
- 3、十六进制abc转十进制
- 2、十进制转其他进制
- 1)十进制转二进制
- 2)十进制转八进制
- 总结
- 七、字母在计算机中的存储
- 八、汉字在计算机中的存储
- 计算机的存储规则
- 九、图片数据在计算机中的存储
- 1)黑白图
- 2)灰度图
- 3)彩色图片
- 三原色小结
- 解释彩色图片
- 十、声音在计算机中的存储
- 十一、计算机的存储规则小结
一、计算机中的数据存储
在计算机中,只有以下三类数据(文本、图片、声音),而视频是很多图片的组合体。
其中文本又包括了数字、字母、汉字。

在计算机中,任意数据都是以二进制的形式来存储的。
二、十进制
在现实生活中使用的是十进制,十进制就是由0123456789 这十个数字组成,它的计算规则是:逢十进一,借一当十。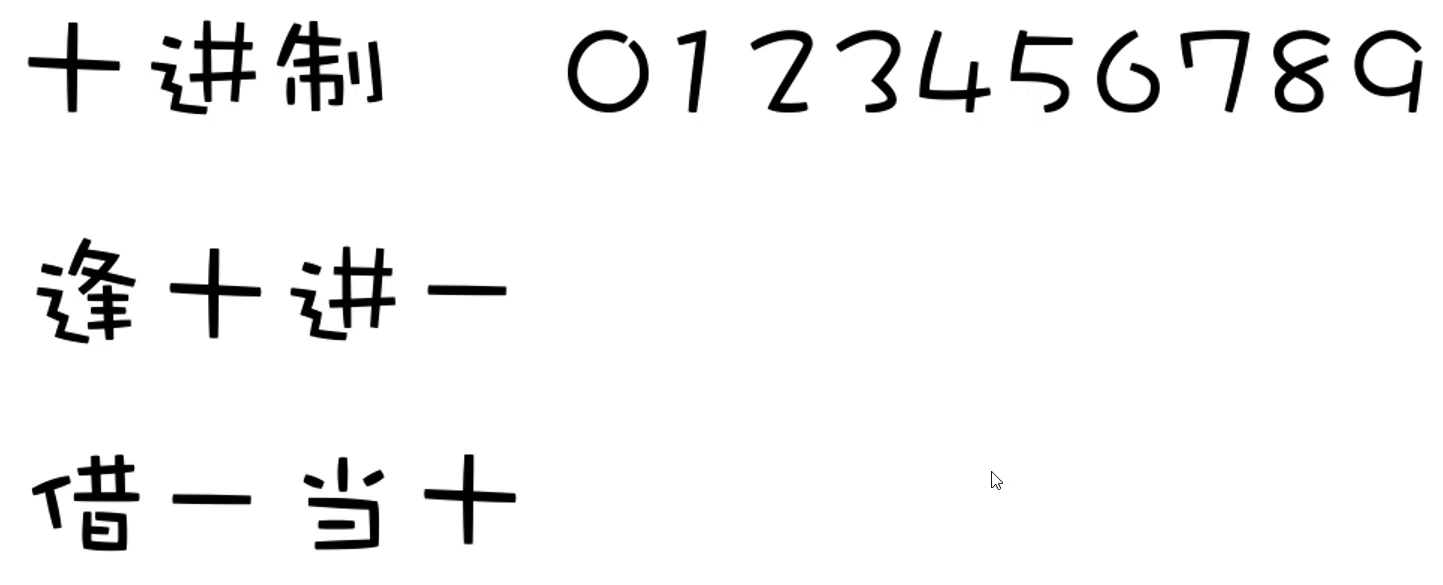
例如:
1、十进制加法
1 + 1,在小学的时候,一般都是竖过来计算的,由于1 + 1是没有超过十的,直接计算即可。
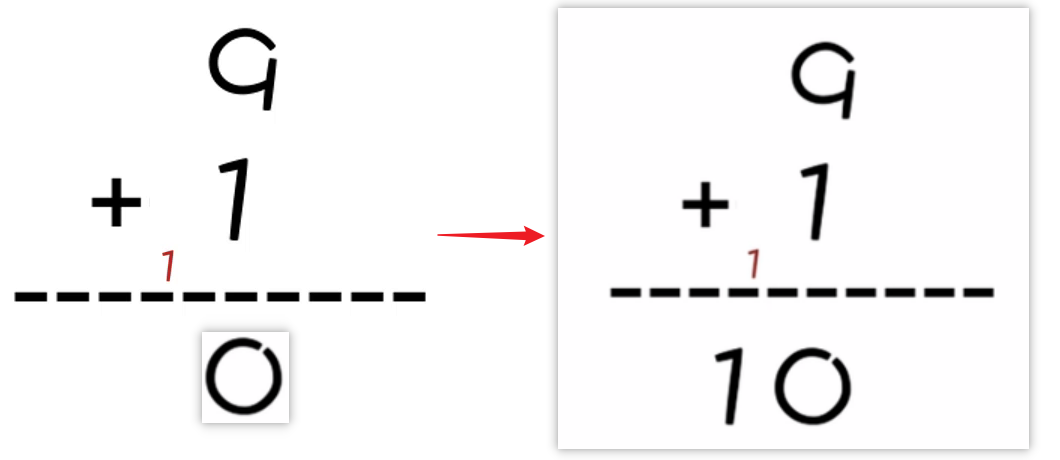
但当数字变成 9 + 1的时候,此时就需要进一了,一旦进一了,个位就变成0了,而十位上没有任何的数字跟进上去的1相加,所以1直接落下来变成1,个位和十位组合在一起,就是个10。
如果是 99 + 1 呢?首先还是从右边的第一位跟下面的1相加,个位变成0,然后逢十进一;然后十位上的 9 跟进上来的 1 相加,结果还是10,然后再往百位进一,十位就变成了0;继续计算百位,百位只有进上来的1,所以百位最终就是1。个位、十位、百位组合在一起,最终的结果就是 100。
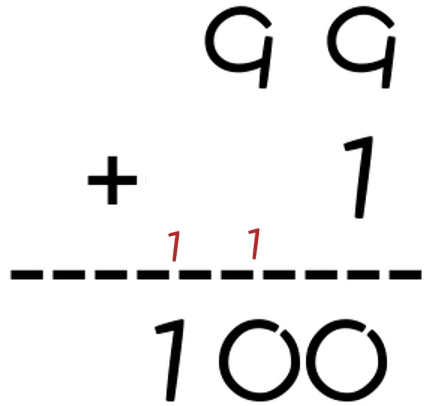
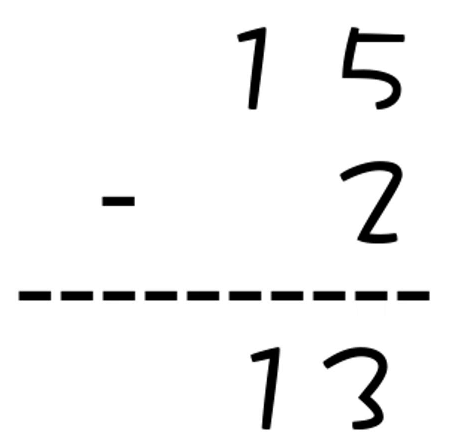
2、十进制减法
例如:15 - 2,个位的5跟2相减,变成3;十位的1下面没人跟它减,直接落下来,最终的结果就是 13。
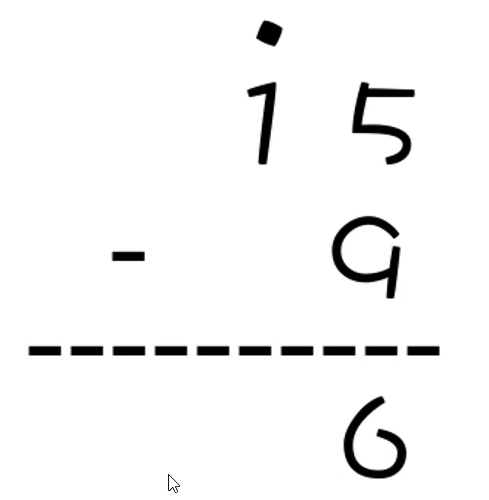
但如果现在数字变成了 15 -9 呢?在一开始,还是个位跟个位减,但是这里 5 - 9 不够,不够就往前借,借过来的1当做10来处理,并且在借的时候,要在被借的地方打个点,因为十位上的1被借走了,所以十位上是没有数字能最终落下来的,所以最终的结果就是 6。
三、什么是二进制?
二进制就是由 0 和 1 这两个数字来组成的,它的计算规则是:逢二进一、借一当二。

二进制的运算过程
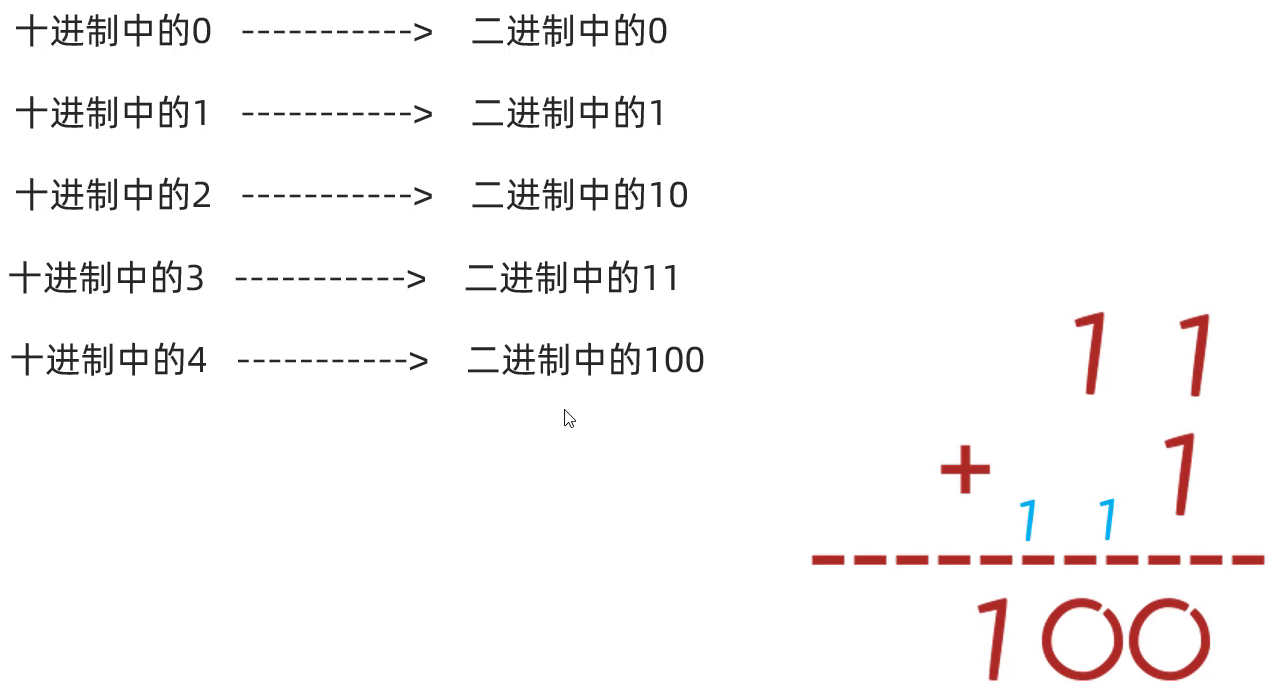
有个梗:1 + 1 在什么样的情况下不等于2?在二进制的时候不等于 2,而是等于 10,因为逢二进一。

十进制中的3就是在2加一,变成 11,十进制中的4,就是 11 + 1,在计算的时候也是从右往左计算的,个位1 + 1,逢二进一,一旦进位了,那么原来位置上就变成了0,前面的位置上会有个进一(蓝色的数字);进一后,跟原来的位置上的数相加加完后,又变成了2,此时继续进1,最终的结果就变成了 100。
四、常见的进制
除了十进制和二进制外,还有八进制和十六进制。八进制和二进制是类似的,它是由 0-7 组成的,缝八进一。十六进制就是缝十六进一,它是由 0-9 和 a - f 组成。
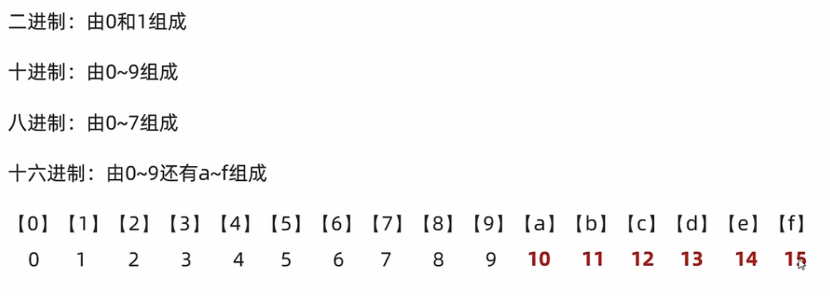
这么多进制就有可能会出问题,比如说我在代码中书写一个 1,那你怎么知道这个1是多少进制呢?因此,Java给这些进制还做了一些规定,这种规定是在JDK7的时候才提出来的。
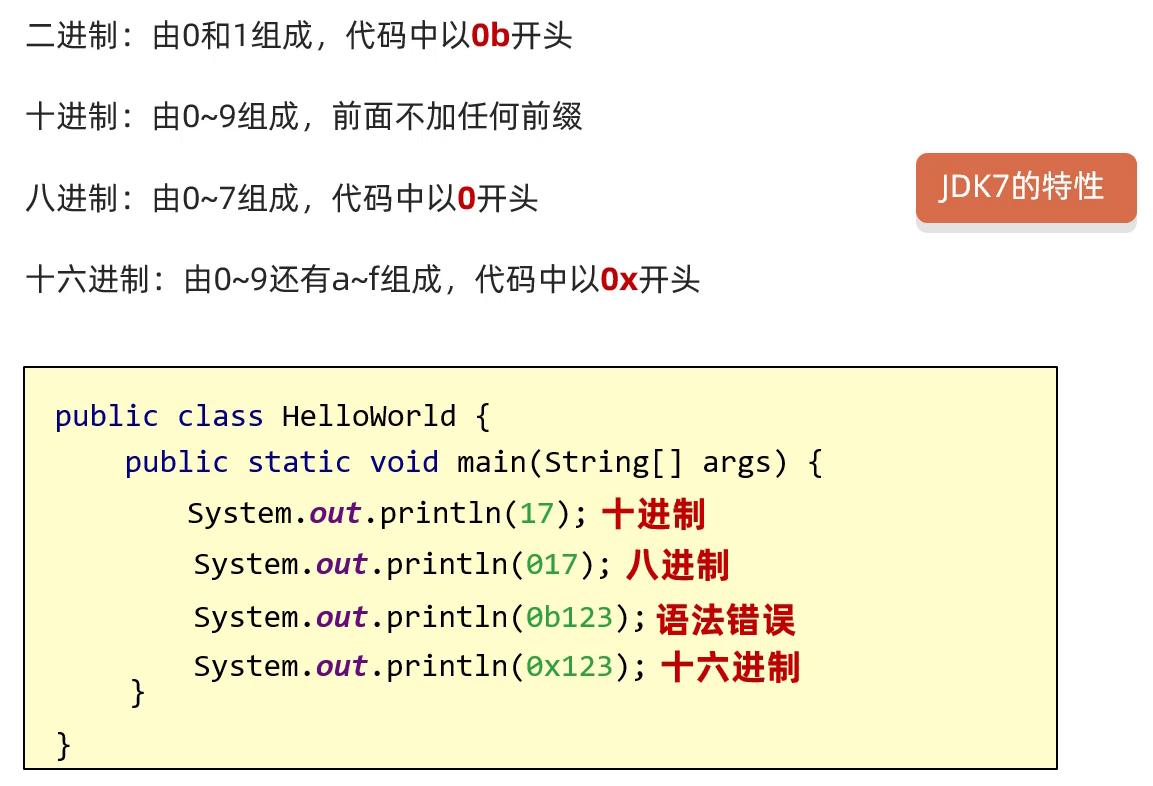
五、计算机为什么要用二进制存储数据?
下图是上个世纪计算机所用到的打孔纸带,这个纸带其实就是我们自己书写的代码,其中打了孔是0,没打孔是1。感兴趣的朋友可以搜索一下 IBM 29卡打孔机 相关视频,看完视频会理解更加通透。

如果我现在想让计算机去执行代码,就得把这个纸带去给计算机。

计算机一遍读取程序,一遍在纸带上打孔,然后在计算机上方会打印出程序运行的结果,例如下图就是一台1958年的电脑顺着纸带打印的程序运行的结果。

在以前,想要编程,必须先准备一个很长很长的纸带,然后用打孔器去打孔。但是如果手抖,打错了怎么办?所以在以前,程序员有两个神奇:胶水、改正纸,如果一不小心多大了一个孔,就用胶水和改正纸把孔给补上,但是如果错的太多,就只能重新打孔。这个就是上个世纪60年代的计算机,因为在纸带上面,只有两种状态:有孔和没孔,所以说在当时,计算机就使用二进制的形式来表示的。
那你想,如果当时用十进制去表示,那怎么在纸带上去表示十个完全不一样的状态呢?如果有人说将一个圆只打1 / 2、1 / 4等去表示不同的状态,这肯定不行,因为看左右图纸带上的孔,它只有一丢丢打,在当时计算机也没有那么精密,是区分不了孔的大小的,它只能区分有孔和没孔这两个状态。

而这个习惯在我们现在计算机中也延续了下来,例如右图的这种电路板,平时在计算机里,用的更多的是那种5V的电路板,所以说就有个规定,会把大于3.3v的定为1,小于3.3V的定为0,这个就是2进制的由来。

所以说计算机为什么使用二进制去存储数据,就是因为只要两种状态就可以表示二进制,在以前是有孔和没孔,在现在是高压电流和低压电流。那如果在计算机里要用十进制去表示,就需要十个完全不一样的状态,这个就太麻烦了。
六、进制之间的转换
进制之间的转换可以分成两种:1、任意进制转十进制;2、十进制转任意进制
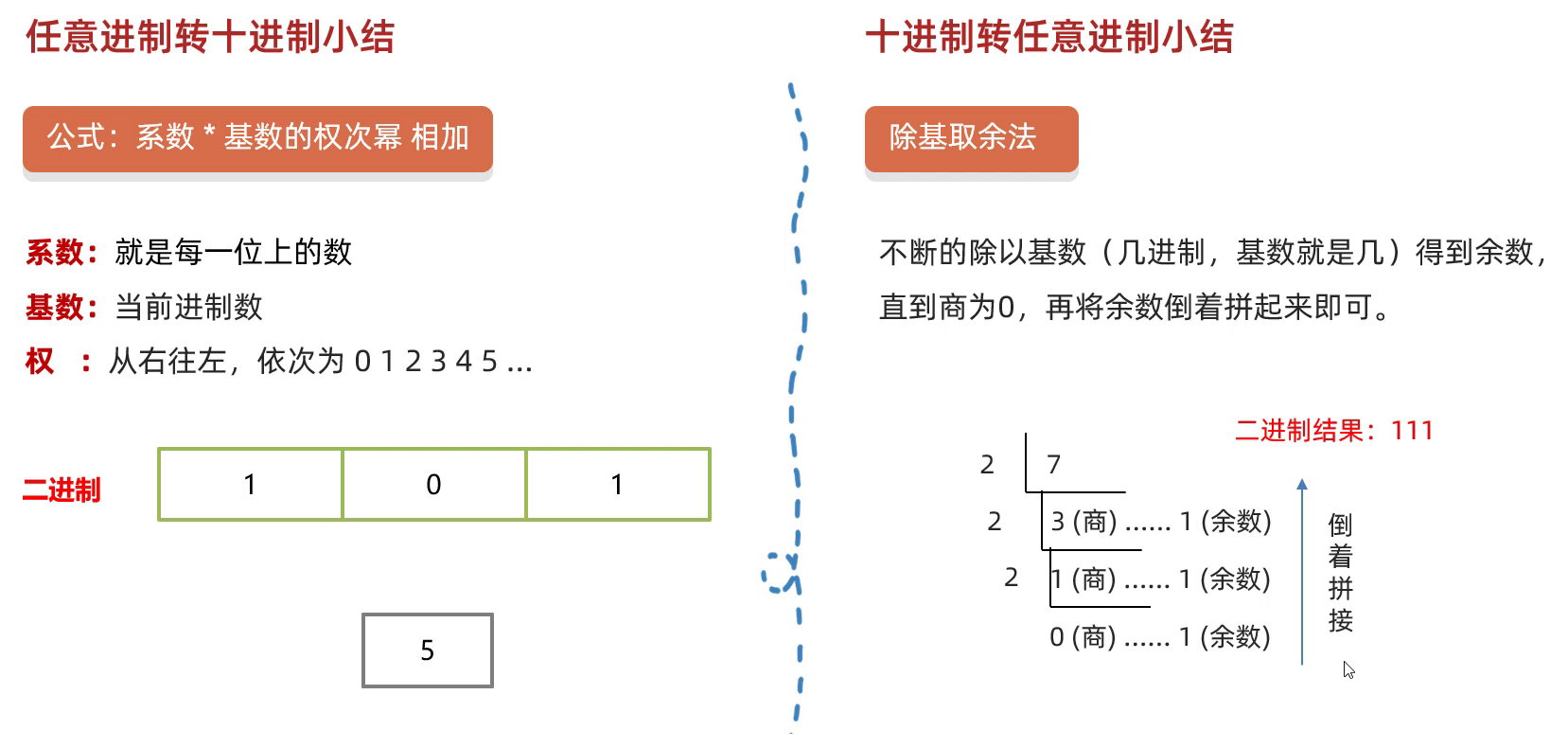
1、任意进制转十进制
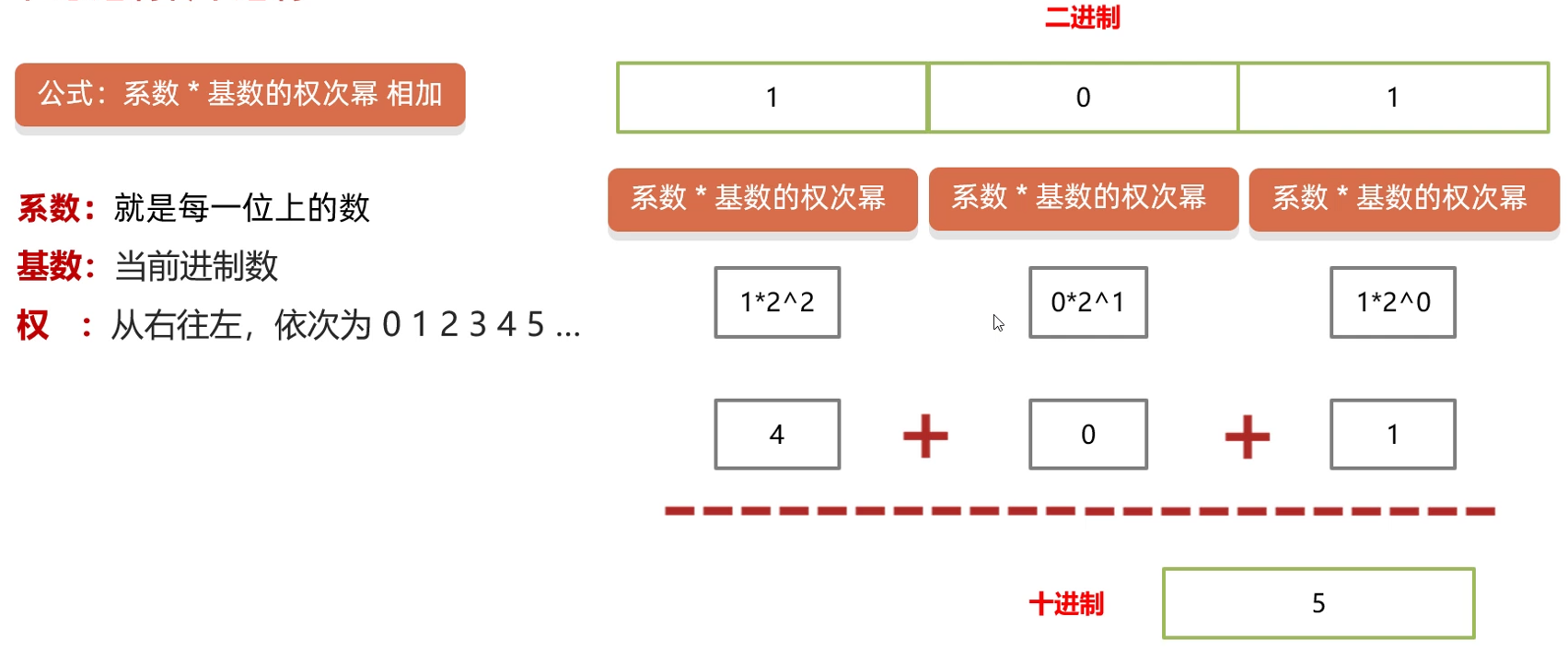
公式:系数 * 基数的权次幂,然后将每一位相加
系数:就是每一位上的数
基数:当前进制数,例如:将2进制转为十进制,基数就是2
权:从右往左,依次为 0 1 2 3 4 5 …依次递增
1)二进制101转十进制
第一步:将每一位都按照系数 * 基数的权次幂算出来,算完后得到三个结果,最终再相加就行。
-
右边的第一个因为右边的数字是1,所以它的系数就是2,又因为当前是二进制,所以基数就是2,权是从右开始,0、1、2…依次递增,所以右边的第一位就是0。
-
同理,再看中间这一位,系数是0,因为当前位置上的数是0,基数是2,因为当前是2进制,权是1,因为它是从右往左是第二位。
-
左边这位,系数是1,基数是2,权是2。
此时我们就可以将上面三个数据分别计算出来,然后相加,得到最后结果5,所以二进制 101 转成十进制后就是 5。
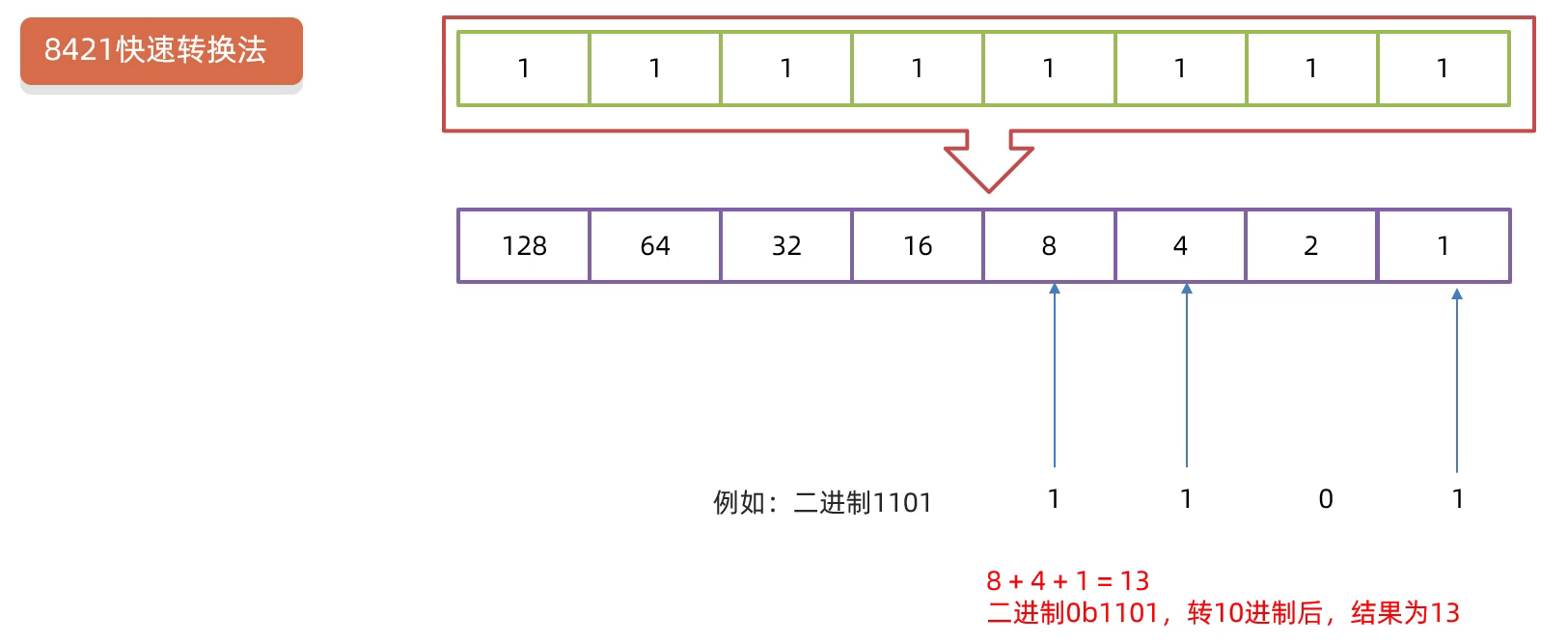
但其实,二进制转十进制有一种快速的转换方法,这种方法叫做8421快速转换法。
8421快速转换法
每一个二进制值的1都是代表一个固定数值。把每一位的1代表的十进制数加起来得到的结果就是它所代表的十进制数。
例如:给二进制 11111111 制定一张表,在这张表中,它每一位所对应的数字从右往左对应的十进制列出来。如果我现在要将二进制的 1101 转为十进制怎么办?解答:拿着 1101 到这张表里去查,有1直接对应它的十进制数,如果该位是0就不用管,然后将对应的数字拿出来,然后相加。所以此时我们就可以认定二进制 1101 转成十进制后,结果为13
2)八进制101转十进制
同样的也是带入公式即可。系数还是每一位当中的数字,基数就是当前的进制,但是当前是八进制了,所以基数就变成了8。权的规则还是和刚刚一样,从右往左,分别是0、1 、2 、3…
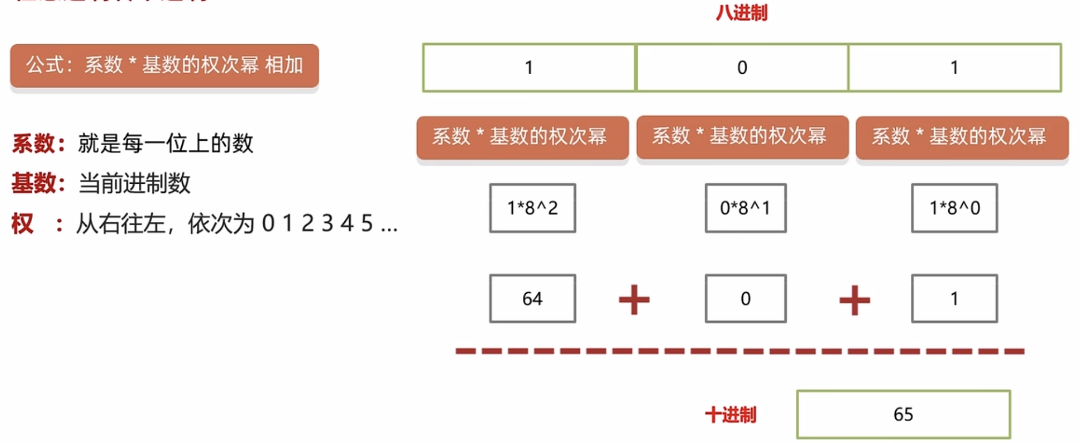
3、十六进制abc转十进制
-
右边位:因为当前位数字是c,所以系数是12。又因为当前数字是十六进制的,所以基数是16。权从右往左开始,它是0。
-
中间位:当前的数字是b,b所对应的数字是11,所以这里的系数就是11。当前是十六进制的,所以基数是16。权从右往左开始,当前是1。
-
左边位:同理,系数是10,因为a所对应的数字是10。基数是16,权是2。
最终将上面计算出的结果相加,十六进制 abc 转十进制得到的结果为 2748。
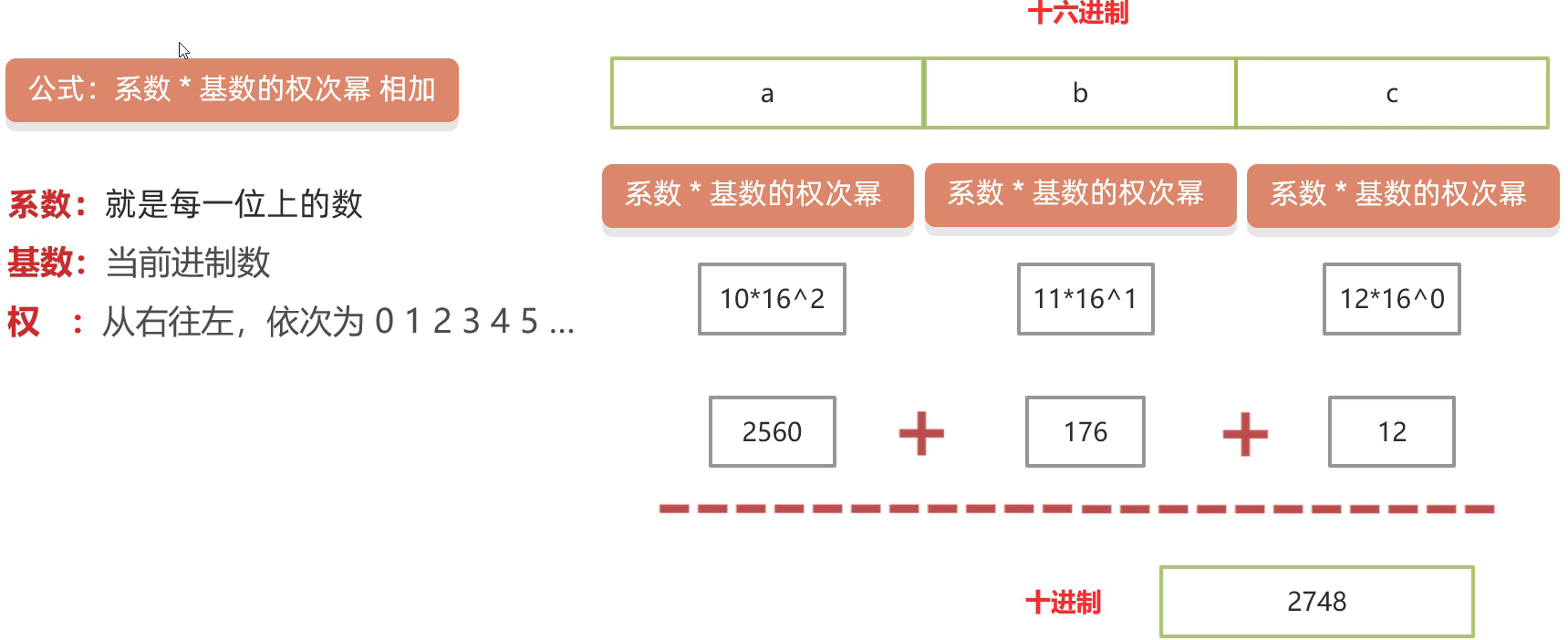
2、十进制转其他进制
解决方案:除基取余法。不断的除以基数(几进制,基数就是几)得到余数,直到商为0,再将余数倒着拼起来即可。
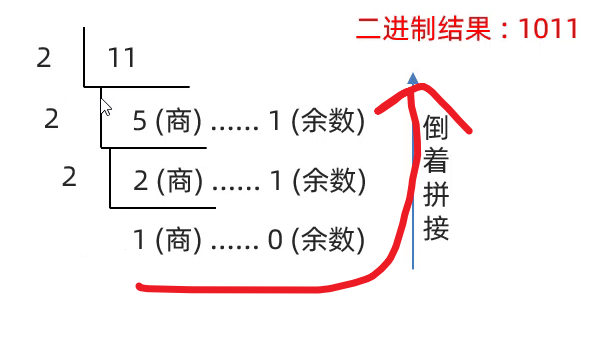
1)十进制转二进制
例如十进制 11 转二进制,直接拿着11不断除以2即可。7转二进制也同理。

在有些资料中在相除的时候不会除到商为0,它偷懒了,商到1就结束了。然后再从商倒着拼接,也是 1011,这种计算方式也是可以的,只不过它是偷懒了,并不是正统的解法。正统应该是一直除,除到0结束,然后所有的余数拼接起来,这个才是最正确的解法。
2)十进制转八进制
跟二进制同理,在除的时候不要除2,除8就行了。
总结
此时,你已经对二进制已经了解了,并且对数字的存储,你也已经了解了,简单一句话就是转成二进制,再进行存储。例如 99 转成二进制就变成 0110 0011,但其实这个东西并不需要你去口算,刚刚说的进制的转换,其实是给大家增加见闻的,真的要算可以使用电脑的计数器。
打开计算器,然后切换到程序员模式,展现的数字从下到上分别为:二进制、八进制、十进制、十六进制,点击需要输入的数字的进制类型,然后输入数字即可。
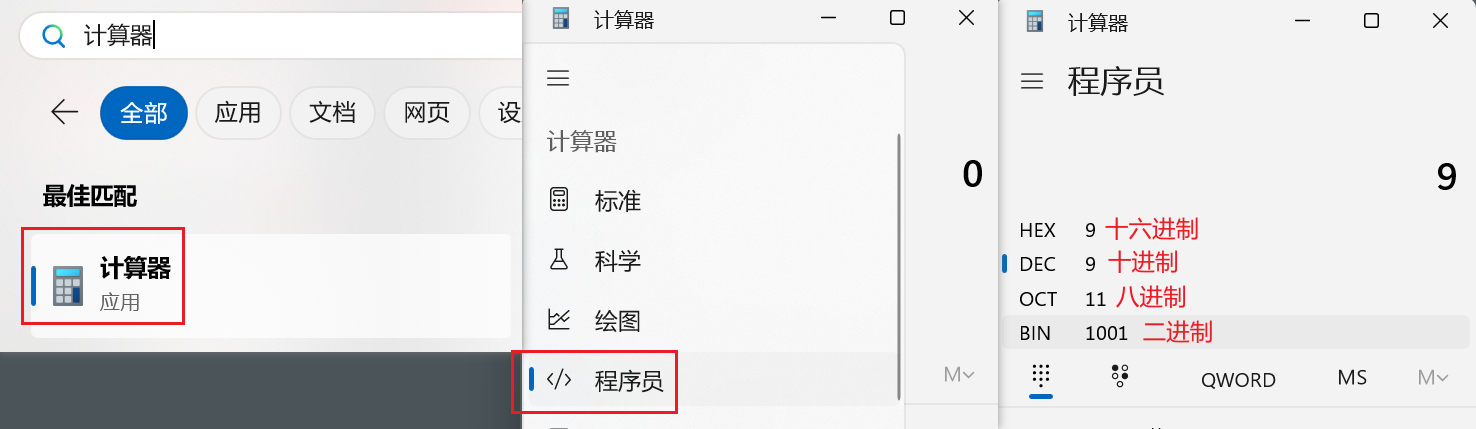
例如计算十进制 99 的二进制是多少:点击DEC,然后输入99,再点击BIN,在最上方出现的就是十进制 99 转二进制后的结果。
七、字母在计算机中的存储
字母跟二进制又是个什么关系,怎么就对应起来的呢?说到这里,我们就要说到一张码表,它的全称叫做 American Standard Code for Information Interchange(没过信息交换标准码表),但我们在说的时候不会说它的全称,太长了,我们会把每个单词的首字母拿出来,进行一个缩写,就变成了 ASCII码表,在 ASCII码表 中,每一个字母都跟一个唯一的数字产生对应关系。
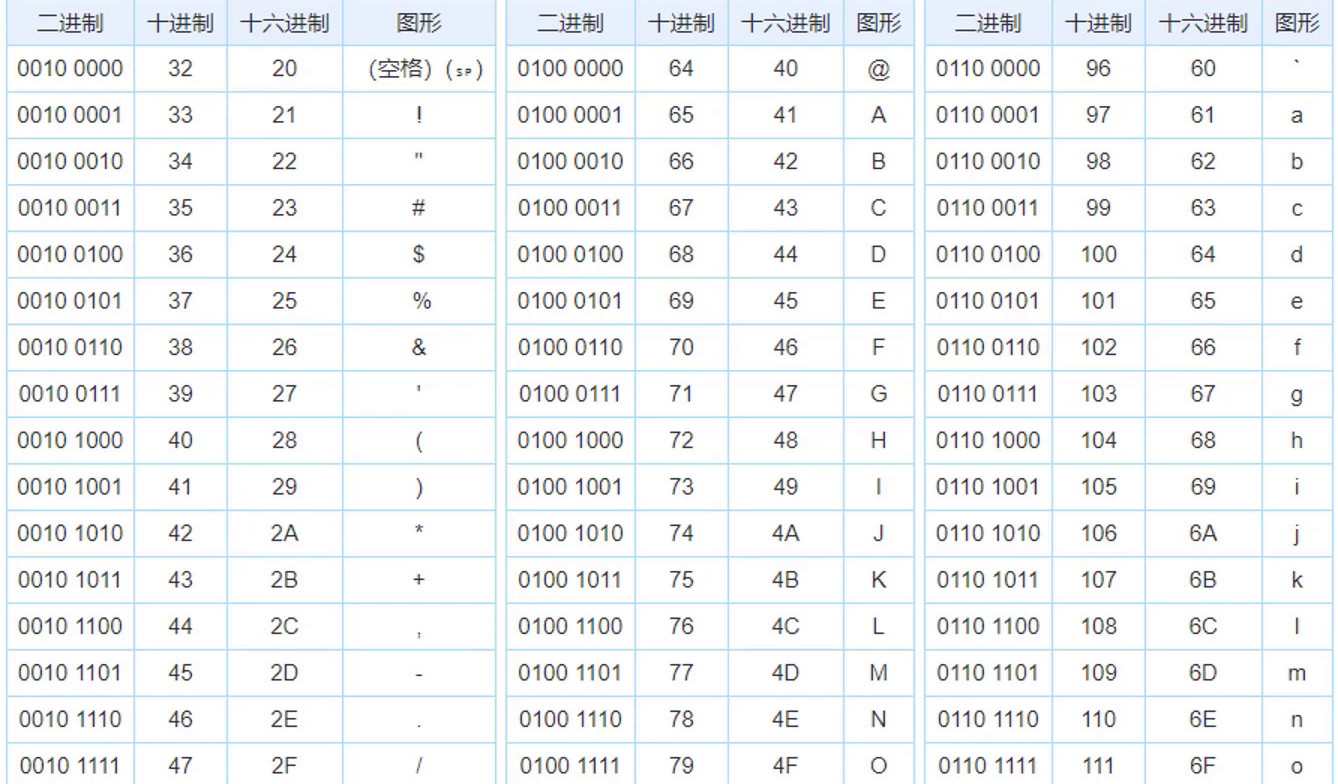
例如字母a,十进制对应的是97。
所以字母在存储的时候,就是通过查询ASCII码表的方式来进行存储的,找到对应的数字之后,再把它变成二进制存储到计算机中。
八、汉字在计算机中的存储
由于ASCII码表是外国人创造的,它在创造ASCII码表的时候并没有考虑到中文。就是因为这,中国的汉字差点就灭了,感兴趣的同学可以自行百度,由于涉及到历史和政治的原因,在这里就不说了。我们一直说的 秀 就是代表人物之一。
为了解决汉字在计算机中的存储问题,在上个世纪80年代,我们国家自己推出了一张 GB 2312。看这个纸它都黄了,我相信比大多数同学的年龄还大。在这张码表当中,它就规定了汉字跟一个唯一的数字会产生一个对应关系,从这个时候开始,汉字才能在计算机中进行存储和运行。

计算机的存储规则
1、GB2312编码:1981年5月1日发布的简体中文汉字编码国家标准。收录7445个图形字符,其中包括6763个汉字。
过了几年,台湾地区也仿照大陆,自己推出了一个BIG5码表,在这个码表当中,它收录的都是一些繁体字,要注意的是,在 GB2312里只有简体中文,是没有繁体的。所以这就出现了一个国家,有两张码表。
2、BIG5编码:台湾地区繁体中文标准字符集,共收录13053个中文字,1984年实施。
但是这可不行,一个国家怎么能有两张码表,都不统一。于是在2000年3月17日推出了一张GBK码表,GBK码表也是目前windows操作系统默认使用的码表。
3、GBK编码:2000年3月17日发布,收录21003个汉字,包含国家标准GB13000-1中的全部中日韩汉字,和BIG5编万码中的所有汉字。
但是还是有点小不足,因为像一些非洲国家,或者是欧洲国家的文字在这张码表里面还是不包含的,因此在后来,有一个国际组织:美国国家标准协会,它提出了一个 Unicode码表,这张码表称之为:万国码,号称一万个国家的码表,这里的万只是一个虚词,它就表示在这个码表当中,包含了世界上大多数国家的文字。
4、Unicode编码:国际标准字符集,它将世界各种语言的每个字符定义一个唯一的编码,以满足跨语言、跨平台的文本信息转换。
正是因为有了这些包含中文的码表,中文才能够在计算机中起飞,而且以后会飞的越来越好,越来越高。
简单来说,数字就是转成二进制,字母跟汉字都是查询对应的码表,先找到对应的数字,再转成二进制进行存储。
接下来我们再来研究,第二类数据:图片数据。

九、图片数据在计算机中的存储
图片数据在计算机中分为三种,从左往右分别是:黑白图、灰度图、彩色图。

要说到图片数据在计算机中的存储,还得来说一说显示器中的三个知识点:分辨率、像素、三原色。
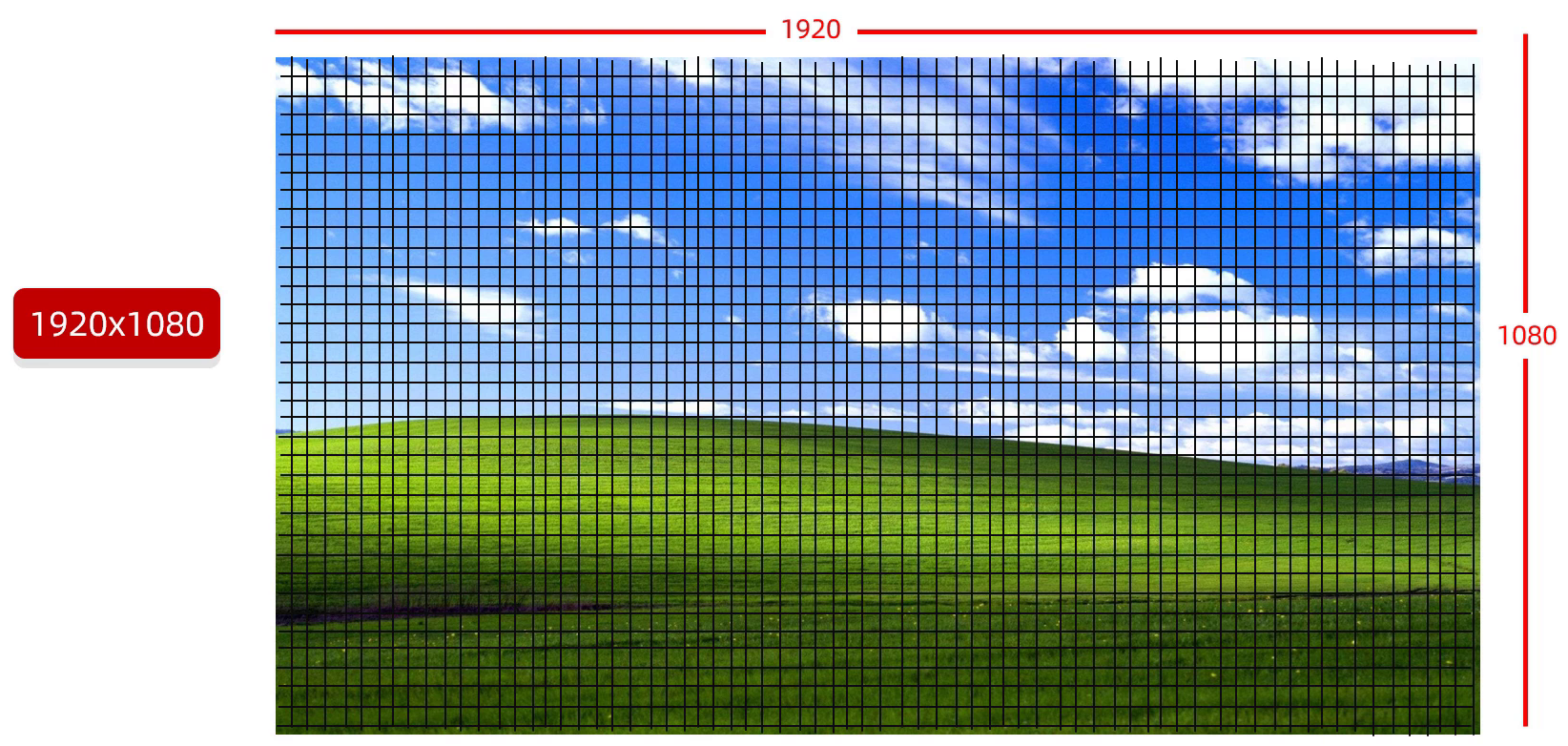
说到像素,就要说到显示器,在平时电脑显示器当中,见到的最多的就是:2K屏、4K屏,但其实这说的是它们的最大分辨率。
2K屏的最大分辨率有:1920 × 1080、1998 × 1080、2048 × 1080、2048 × 858。
而右边的4K屏最大分辨率有:3840 × 2160、3996 × 2160、4096 × 2160、4096 × 1716。
其中最为常见的是2K屏中的 1920 × 1080、3840 × 2160。

下面以1920 × 1080 来讲解一下这些分辨率表示什么意思。
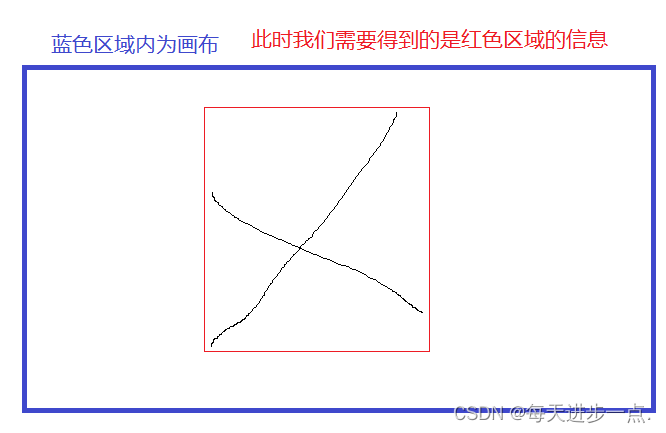
其实就是表示,在显示器中,宽有1920个小格子,高有1080个小格子,整个显示器就是由这么多方形的小格子来组成的,而这里的每一个小方格就称之为一个像素。
我们也可以在屏幕上画一笔,然后再把这一笔放大,此时可以发现这个图片的周围会有锯齿,就是因为显示器是由很多很多方形小格子组成的。

如果说我们以后要写一个软件,我们要设置软件的大小,我们现在会设置软件的宽为514像素,高为595个像素,它差不多占屏幕宽度的1 / 4,高度的1 / 2。如果说我想要这个软件变大一点,就可以将它的宽高调大:宽603个像素,宽可以写680个像素。

在后面,我们会有一个练习,会带着大家去写一个游戏,游戏当中就会用到像素的概念了,所以说当以后,我们开始写游戏的时候,我让你设置宽高为100个像素的时候,我问你这个游戏大概有多大,你不能回答我:大概有这么大,大概有这么宽了。
1)黑白图
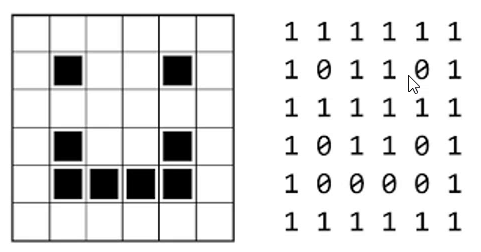
说完像素,就可以来解释黑白图了。在这个黑白图中画了一个笑脸,上面两个黑点表示眼睛,下面一个湾勾,就好比嘴巴。其实在黑白图当中,就是给每个像素点去涂抹了颜色,其中白色就是1,黑色就是0。
2)灰度图
直到灰度图之前,首先需要直到灰度表。在这张表当中,0是纯黑,255是纯白,中间就是一些不同层次的灰。
在下面这张图中,画了一个8,在没有8的地方就视为0,在画了8的地方就显示不同程度的灰色。例如第一排的8就是64、142 、146 、182…组合在一起,就是左边的8。

3)彩色图片
彩色图片是我们平时见过最多的,那这个彩色图片又是怎么记录里面的色彩的呢?其实跟刚刚也是类似的,下面就将图片嘴唇的位置进行放大。

在彩色图中,其实就是我们在给一个像素点里记录不同的颜色就可以了,那这个颜色该怎么记录呢?这时就需要先明白三原色(红黄蓝),通过三原色我们就可以搭配出各种各样五彩缤纷的颜色了。这三种颜色我们也称之为美学三原色。

在计算机当中其实也有三原色的存在,它叫做:红绿蓝,这三种颜色称之为光学三原色。
在计算机里面每个像素点的内部,其实就是由红绿蓝来组成的,我们可以讲左边的屏幕放大来看一下。在这里看见的每一个红绿蓝组成的一个整体就是一个像素点,现在就是由很多很多个像素点组成在一起,就组成了一张完整的图片,在计算机中,就是通过三种颜色的搭配,就可以组合出五彩缤纷的颜色了。

所以在这里我们要知道,计算机中的光学三原色是:红绿蓝!
我们可以去给这三种颜色设置不同的值,值越大表示当前的颜色越浓;值越小,表示当前的颜色越淡。
如果说红色设置为43,绿色设置为123,蓝色设置为194,那我就可以理解:由43份红色的颜料、123份绿色的颜料跟蓝色份194份蓝色的颜料,这么一搅和,就可以搭配出不知道怎么描述,但是还挺好看的蓝色。其他形成的颜色也同理。我们在取值的时候,里面的值是不能乱写的,它是由取值范围的,一定要写在 0 ~ 255之间,包含0也包含255。

如果说,我们在指定颜色的时候,写的是这种:(255,0,0),那就表示不用绿色,不用蓝色,只用红色,最终就是纯红色。其他颜色同理。

上面是用十进制的颜色去表示的,同样我们也可以用十六进制的颜色去表示,十进制的255刚好对应FF。所以在十六进制下最小还是0,最大就是FF。
三原色小结
1、在计算机中,颜色是采用光学三原色
2、一个像素点里有红、绿、蓝三种颜色组成,通过这三种颜色的搭配我们就可以组成各种各样的颜色,这个颜色我们取它英文的首字母R(Red)、G(Green)、B(Blue),称这三种颜色叫RGB三原色。
3、可以讲光学三原色写成十进制的表示形式,每一位有范围0 - 255。(255,255,255)
4、当然也可以写成十六进制的表示形式,最小是0,最大是FF。(FFFFFF)
解释彩色图片
有了像素和三原色的知识点,我们就可以解释彩色图片了,在彩色图片当中,每一个像素点就是搭配了不同的三原色从而组成了各种各样漂亮的图片。所以说,在你手机里存储着各种各样让你舍不得删除的图片,其实就是一组又一组不同数据搭配出来的颜色而已,从计算机的角度来看,左边的美女和右边的美女其实它们两个是一样的。

十、声音在计算机中的存储
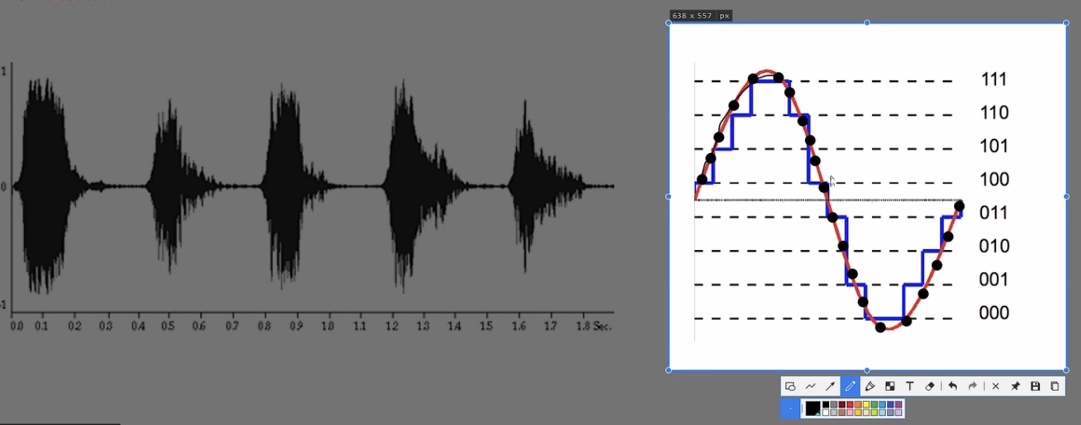
声音的存储会涉及到这种声音的波形图,看右边,这个就是声音的波形图。在波形图中,每一个点都会有每一个数字去跟它对应。
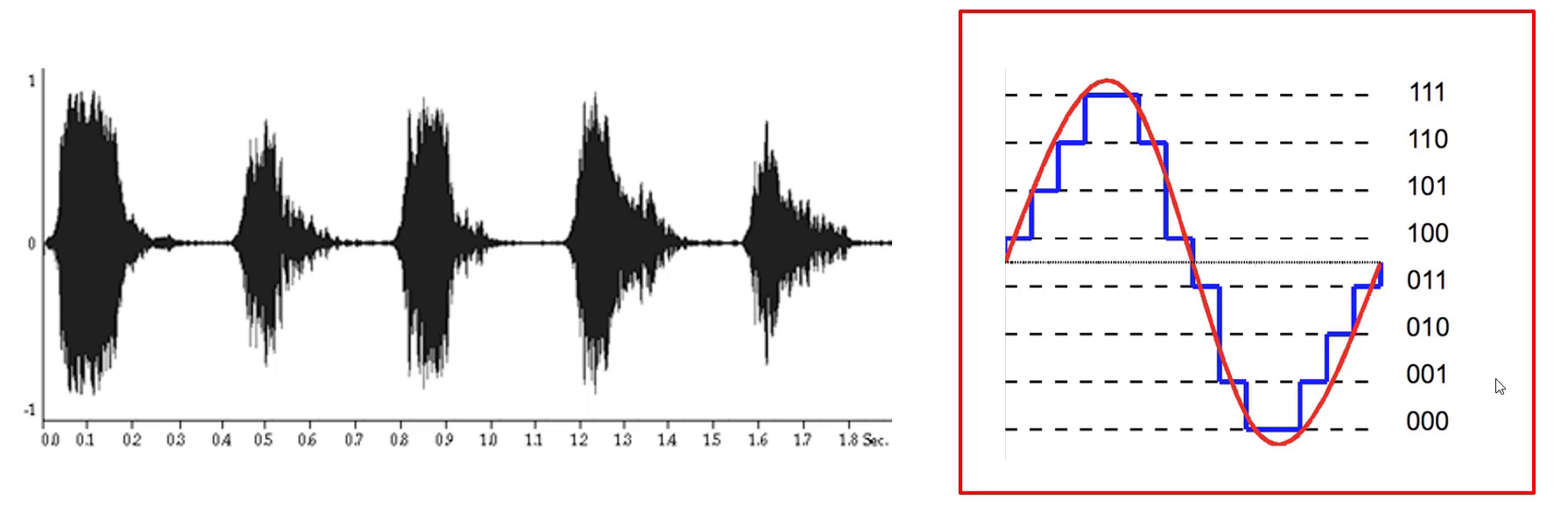
那我们平时在听音乐的时候,如果你氪金了,音质就会非常好,但你的朋友没有氪金,它听的就是全损音乐,那这怎么通过技术来实现呢?其实很简单。
我们在存储声音的时候会对声波进行采样,每个点都会有对应的数字。如果你氪金了,采样的点(比如说下图的黑点)就会比较多,记录的数据也非常的多,在听音乐的时候可以最大程度去还原音乐。
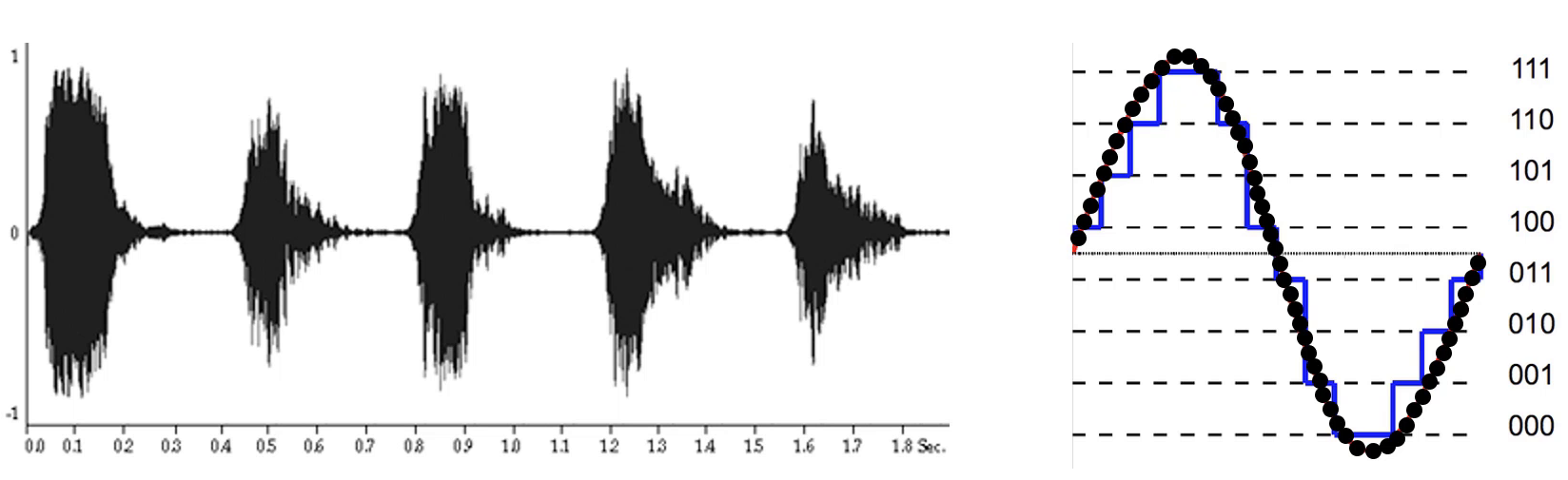
但如果说你的好朋友没有氪金怎么办,此时采样的点就会变的非常的少,那么他在听音乐的时候就是全损音乐,它在还原的时候就不会还原出最原本的声音了。例如在下面这张图中,红色是最原本的声音,但是因为现在没有氪金,采样点比较少,它的还原的时候就不会按照红色的进行还原,而是以你采样的黑点来进行还原。
它在还原的时候就会有这种情况:一直连接黑点,但是在峰值的地方可能无法还原出来,因为在上面是没有对应的采样点的。
十一、计算机的存储规则小结
在计算机中,任意数据都是以二进制的形式来存储的。
在计算机中会有以下的三类数据,分别是:文本、图片、声音。其中文本又包含了数字、字母、汉字。

数字是直接变成二进制来存储的。
字母跟汉字是查询不同的码表,先变成数字,再变成二进制,再来进行存储的,这个码表是不需要你自己去下的,每一个操作系统里都会内置。
图片是通过每一个像素点里的RGB三原色来进行存储的。
声音是对波形图进行采样,然后再变成二进制进行存储的。