＜深度学习入门学习笔记P1＞——《深度学习》

news2024/9/22 9:30:37

一、深度学习概述

1.深度学习入门概念及介绍

在这里插入图片描述
注：
（1）感知机是深度学习网络算法的起源，神经网络是深度学习算法的中心。
（2）损失函数和梯度下降是用来对模型优化和训练的一种方式。
（3）反向传播算法是用来在神经网络中求导用的，用于调整参数和权重。
人工智能划时代事件：
在这里插入图片描述** 深度学习巨大影响：**
在这里插入图片描述

2.什么是深度学习

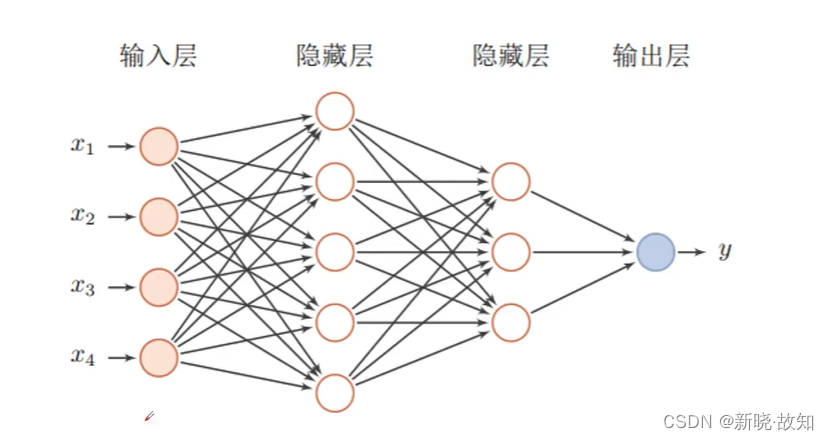
在这里插入图片描述
深度神经网络：
在这里插入图片描述
人工智能、机器学习、深度学习之前的关系：
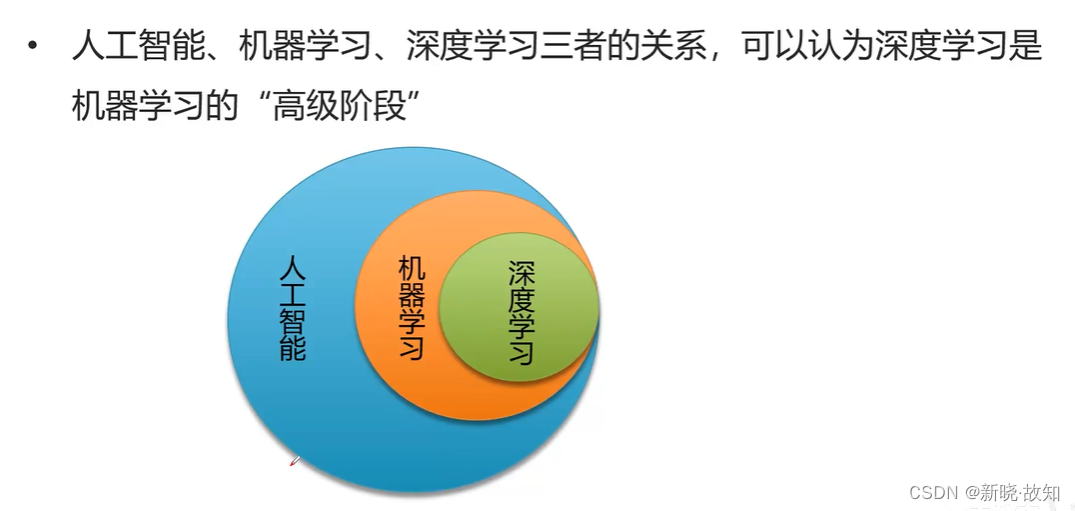
在这里插入图片描述

3.深度学习的特点

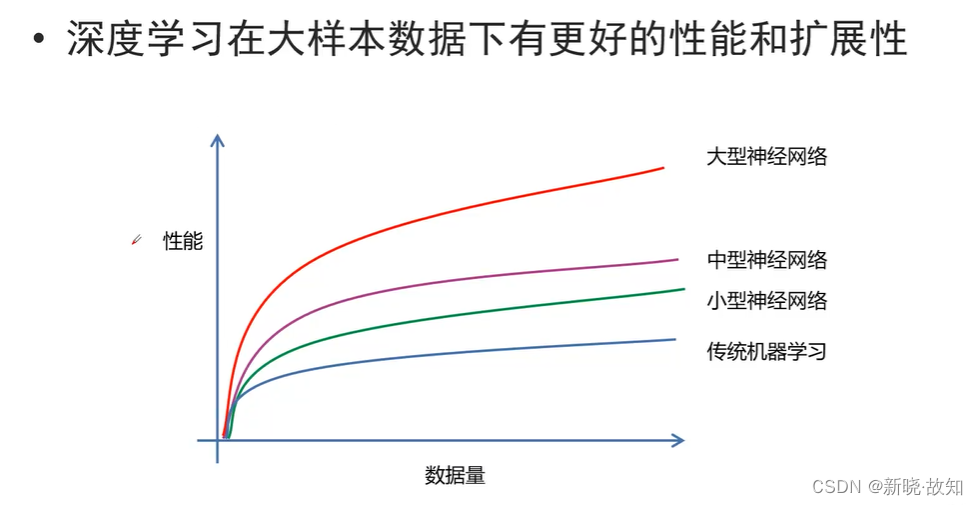
在这里插入图片描述

3.1深度学习的优点

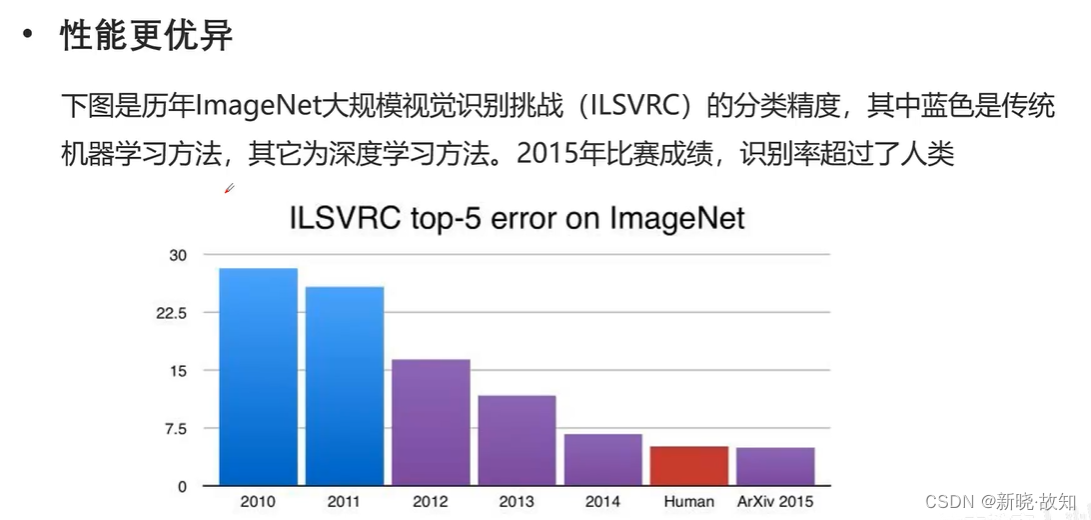
在这里插入图片描述
注：（上图所示的竖轴为错误率）
2011年及之前ImageNet大赛都是采用传统的机器学习模型，2012年之后开始采用深度学习网络模型，如图显示错误率大幅下降。在2015年，深度学习网络模型错误率低于人类平均水平，代表着以机器进行分类的水平已经超越了人类平均水平，直到2017年，ImageNet大赛停办。
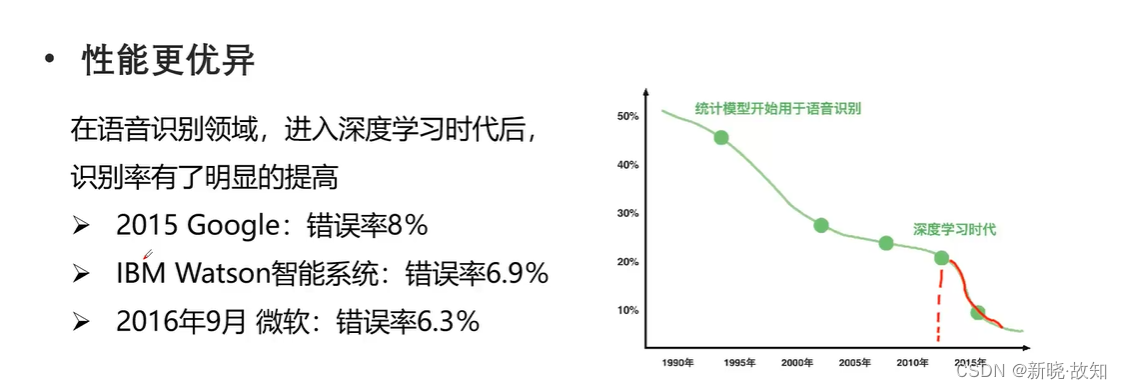
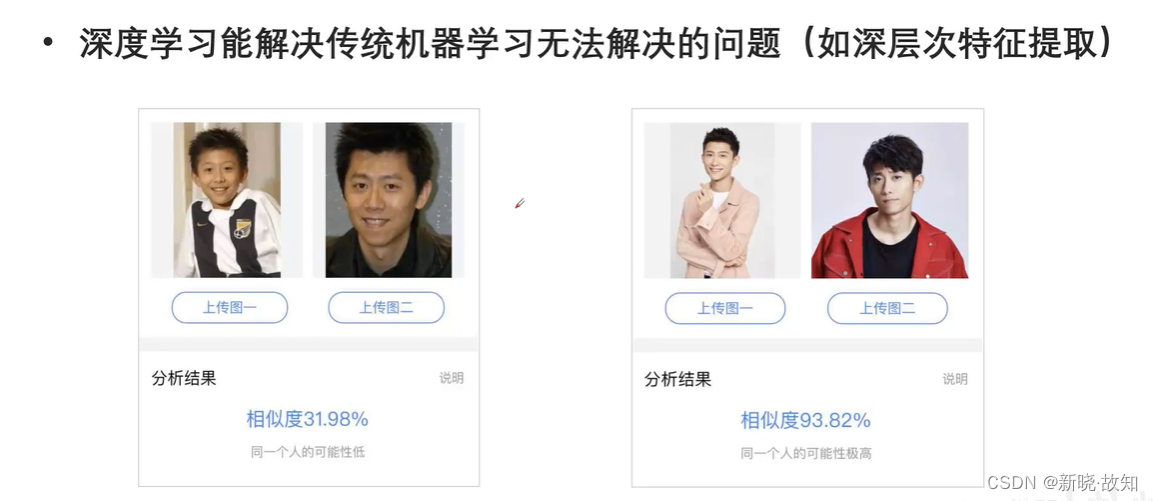
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.2深度学习的缺点

在这里插入图片描述
（1）深度学习需要有大量的数据作为样本进行训练特征提取。
（2）深度学习网络可能会有上千层，构建复杂。
（3）传统的机器学习模型、方程都是自己设计建立的，特征是自己提取的，其过程具有可解释性。而深度学习模型中包含许多隐藏层，有些中间的处理是不可知的。目前，深度学习遇到的一些问题如：通过实验其结果是正确的，而其可解释性较难以解释等，说明其原理比较复杂。类似于量子学等。随着研究的深入，这类问题可能将会得到合理的解释。

4.深度学习与传统机器学习的对比

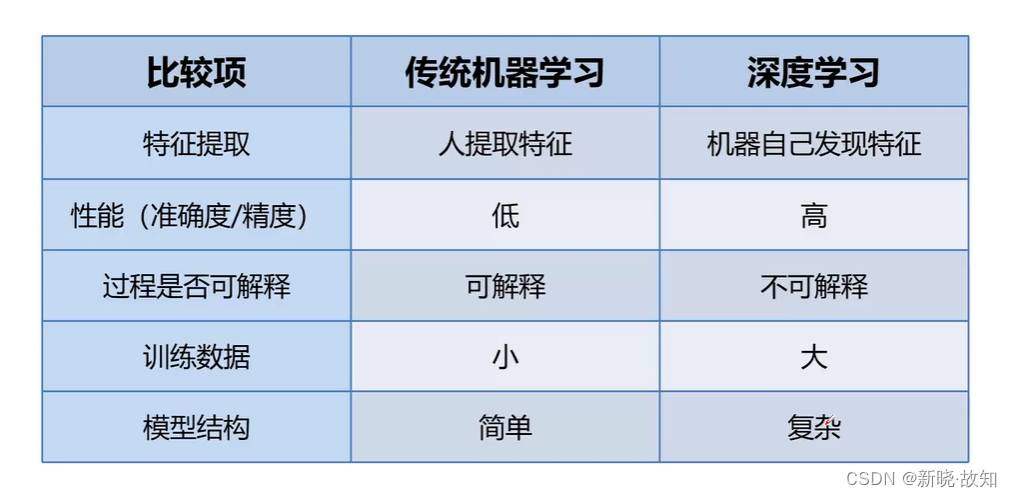
在这里插入图片描述

5.为什么要学习深度学习

在这里插入图片描述

6.深度学习的应用

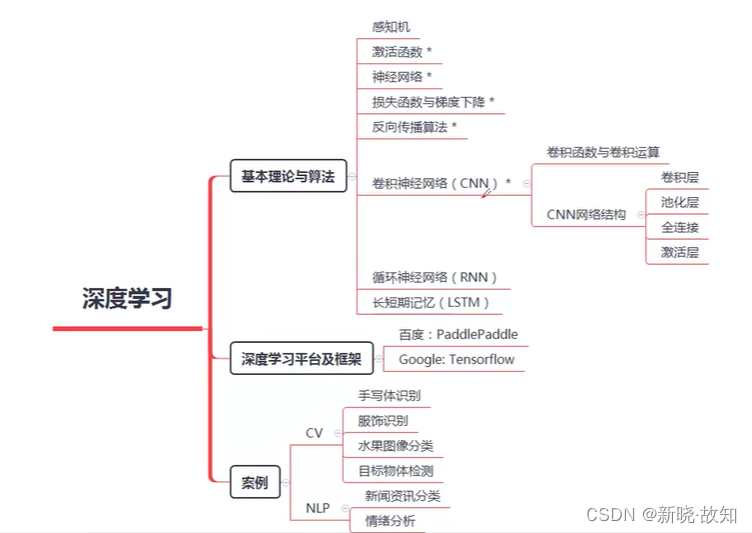
在这里插入图片描述
将要学习的知识：
在这里插入图片描述
课程特点：
在这里插入图片描述

二、感知机和神经网络

1.感知机概述

1.1什么是感知机

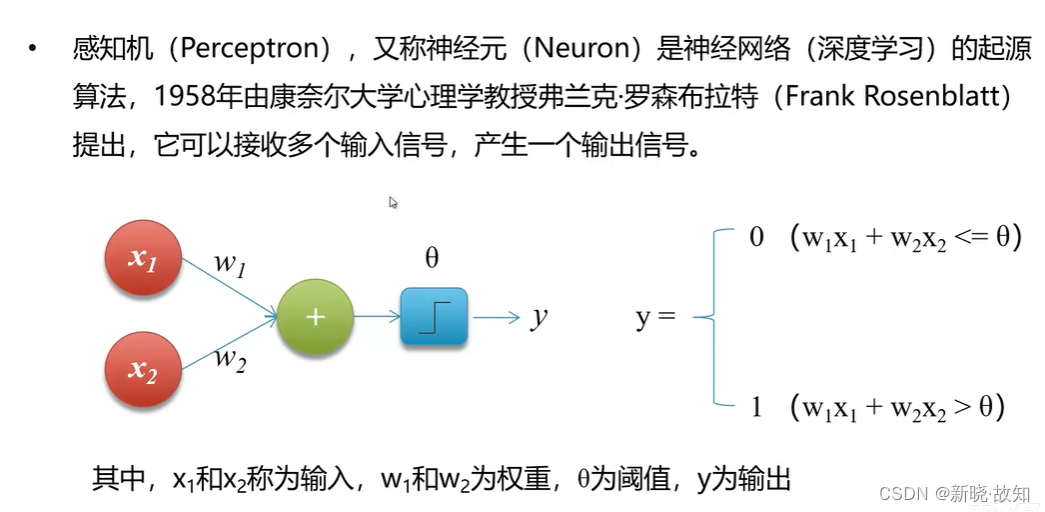
在这里插入图片描述

1.2感知机的功能

在这里插入图片描述
实现逻辑运算：
实现逻辑和：
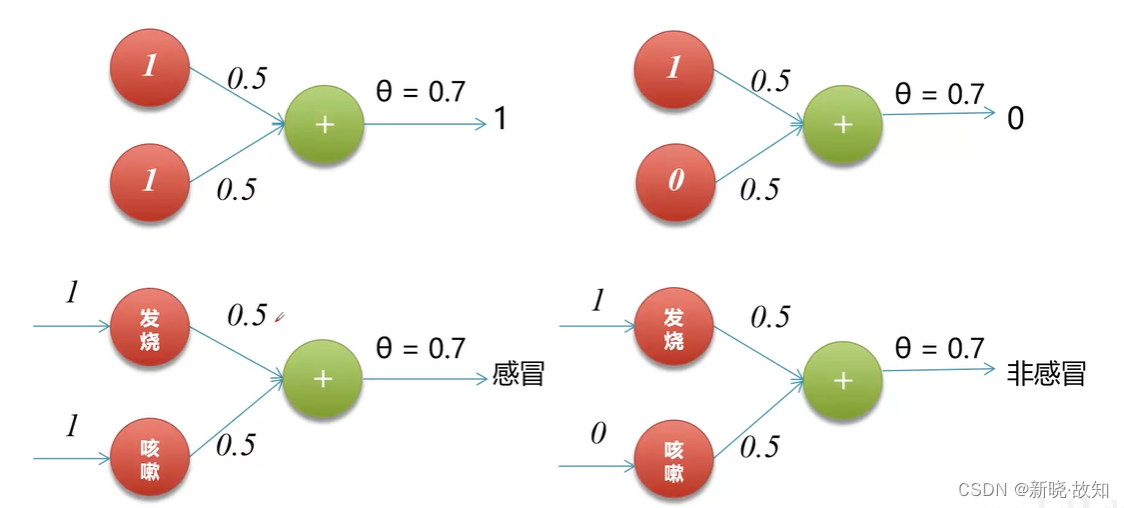
在这里插入图片描述
实现逻辑或：
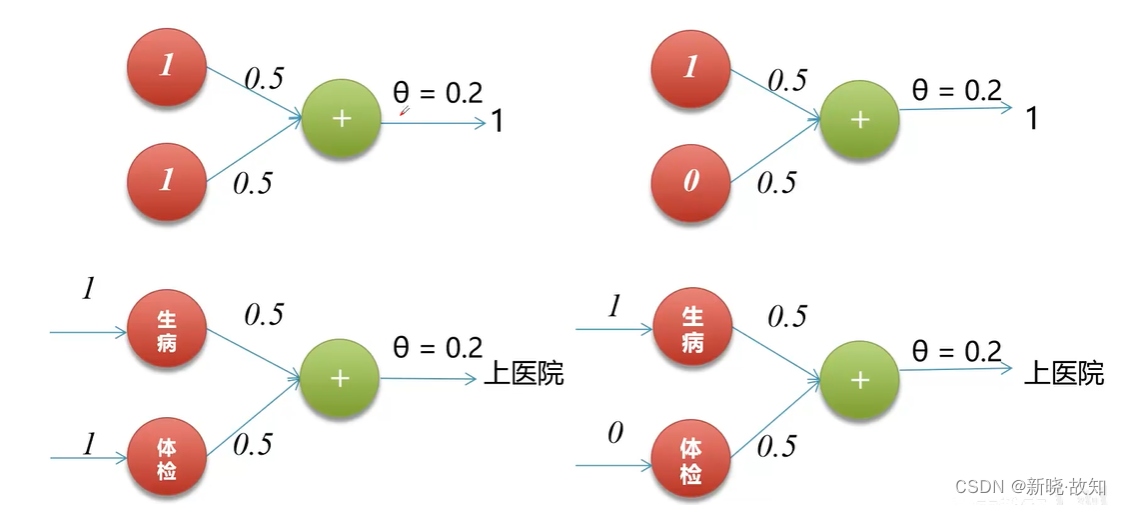
在这里插入图片描述

1.3感知机的缺陷

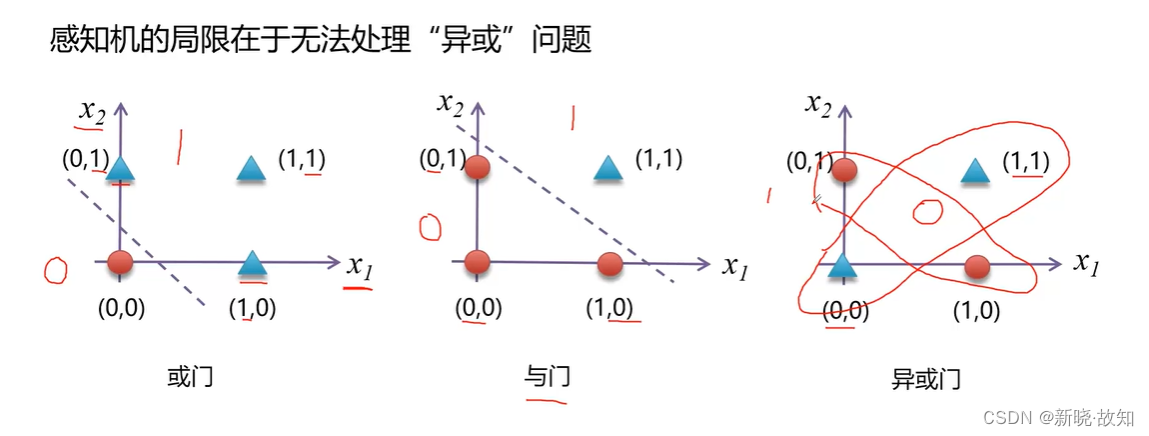
在这里插入图片描述
可以看出，“或”、“与”问题都可以在平面上找到一条直线将其分类，是线性可分问题。而“异或”问题在平面上不是一个线性可分问题，所以通过一个感知机在平面上实现异或问题的处理是无法解决的。

1.4解决方法

多层感知机：
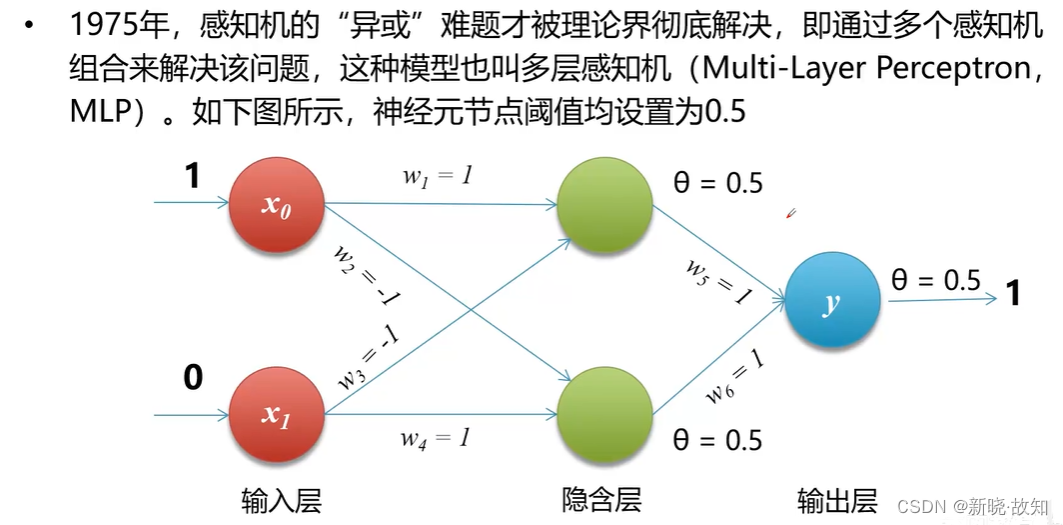
在这里插入图片描述
当输入为1、0演示：
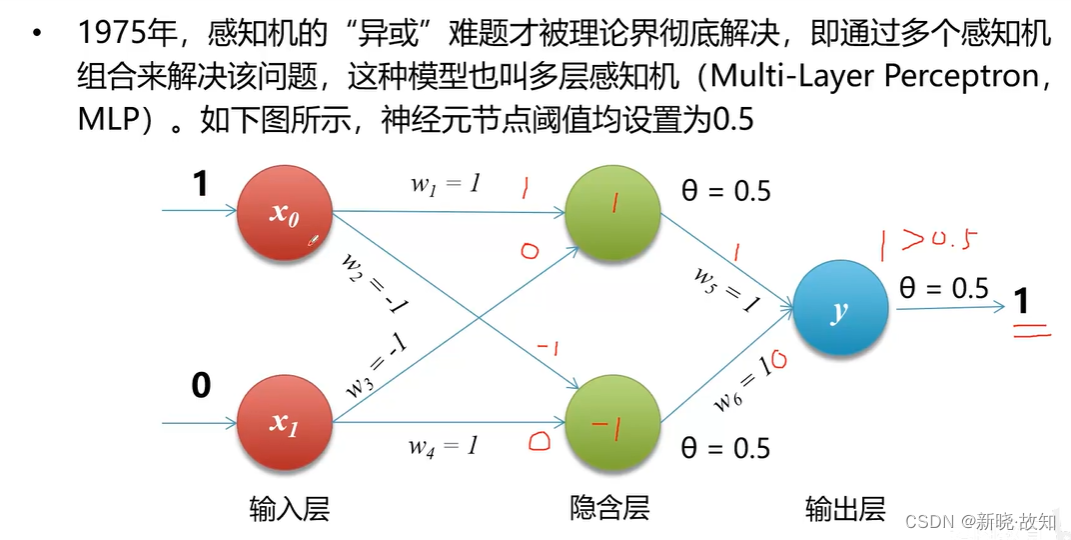
在这里插入图片描述
（因为这个结构是对称的，所以当上面输入0、下面输入1时，也可以输出为1）
当输入为1、1演示：
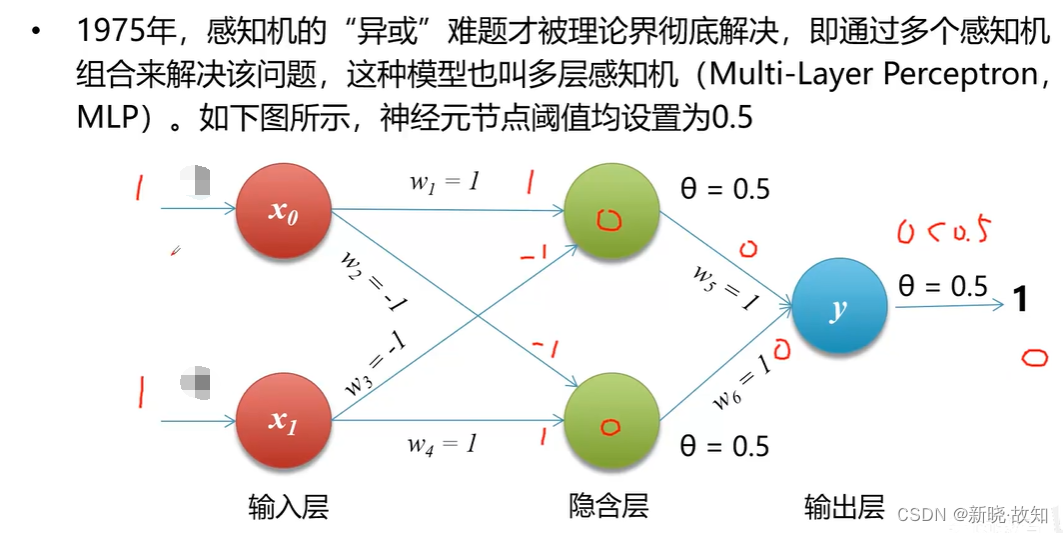
在这里插入图片描述
当输入为0、0易得输出为0，无需演示，即可证明多层感知机解决异或问题。

1.5使用Python模拟实现自定义感知机

# percetron.py
# 自定义感知机

# 实现逻辑和
def AND(x1, x2):
    w1, w2 = 0.5, 0.5  # 两个权重
    theta = 0.7  # 阈值
    tmp = x1 * w1 + x2 * w2

    if tmp <= theta:
        return 0
    else:
        return 1


print(AND(1, 1))  # 1
print(AND(1, 0))  # 0
print(AND(0, 0))  # 0


# 实现逻辑或
def OR(x1, x2):
    w1, w2 = 0.5, 0.5  # 两个权重
    theta = 0.2  # 阈值
    tmp = x1 * w1 + x2 * w2

    if tmp <= theta:
        return 0
    else:
        return 1


print(OR(1, 1))  # 1
print(OR(1, 0))  # 1
print(OR(0, 0))  # 0


# 实现逻辑异或
def XOR(x1, x2):
    s1 = not AND(x1, x2)  # 对x1,x2做逻辑和计算再取非
    s2 = OR(x1, x2)  # 直接对x1,x2做逻辑或计算
    y = AND(s1, s2)
    return y


print(XOR(1, 1))  # 0
print(XOR(1, 0))  # 1
print(XOR(0, 1))  # 1
print(XOR(0, 0))  # 0

2.神经网络

2.1什么是神经网络

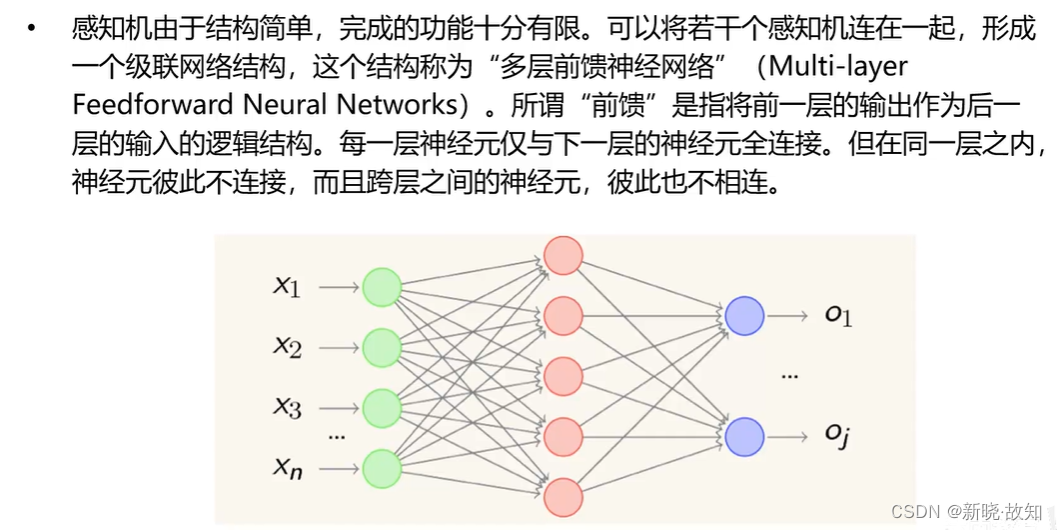
在这里插入图片描述

2.2神经网络的功能

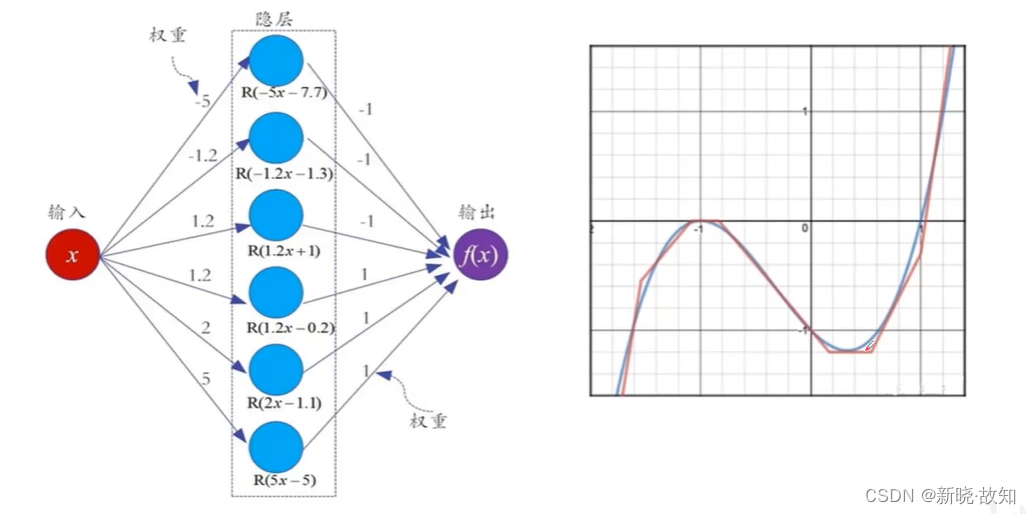
在这里插入图片描述通用近似定理：
在这里插入图片描述
在这里插入图片描述

2.3深层网络的特点

在这里插入图片描述

2.4激活函数

什么是激活函数：
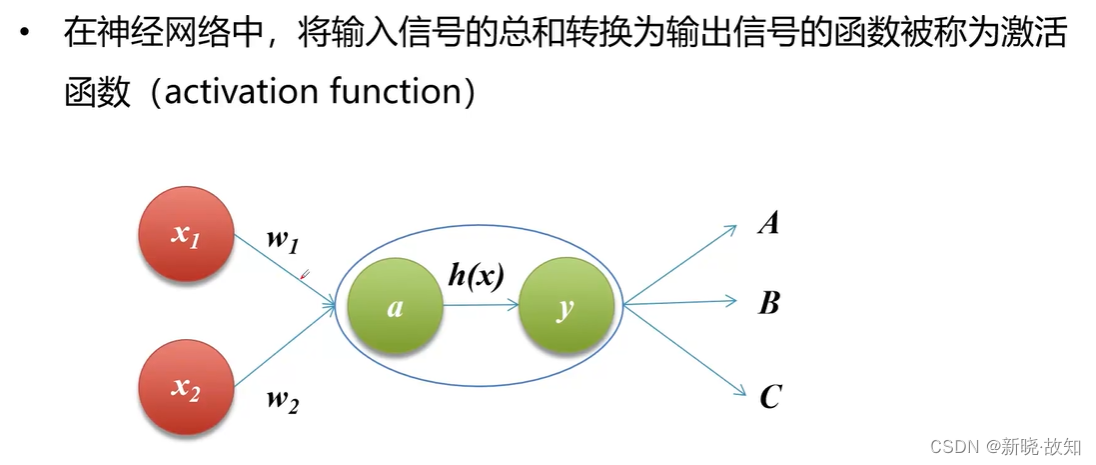
在这里插入图片描述
为什么使用激活函数：
在这里插入图片描述
常用的激活函数——阶跃函数：
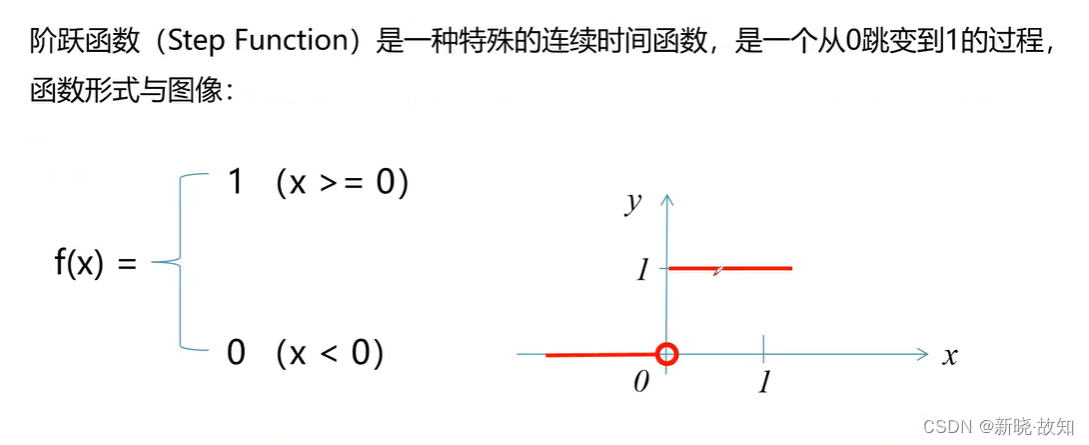
在这里插入图片描述
常用的激活函数——sigmoid函数：
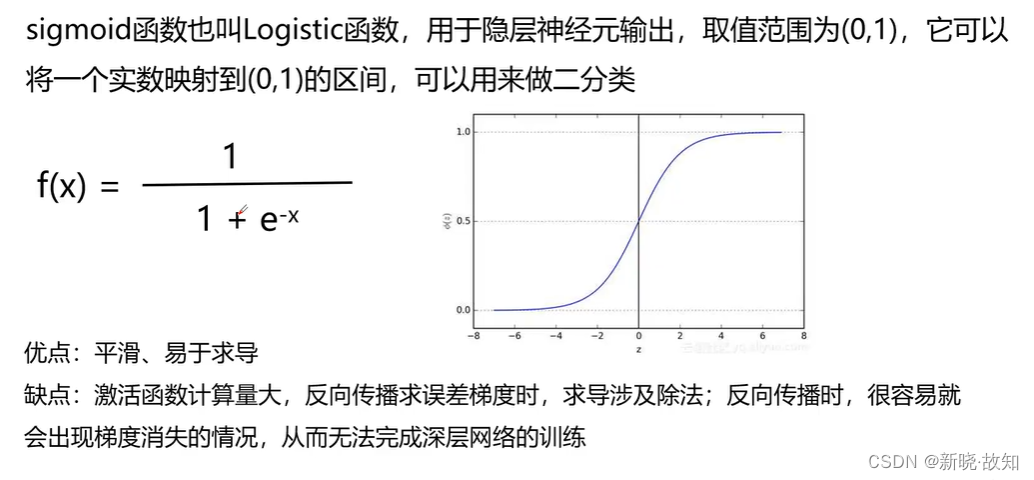
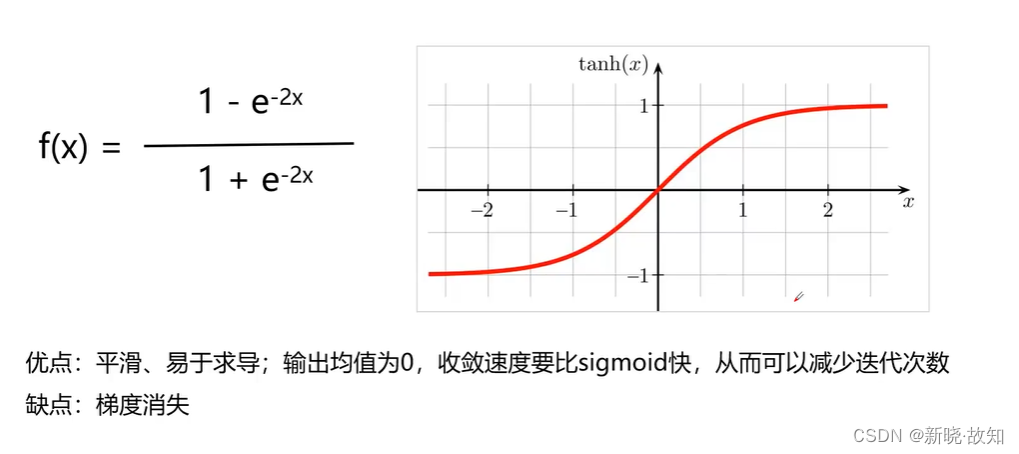
在这里插入图片描述
常用的激活函数——tanh(双曲正切)函数：
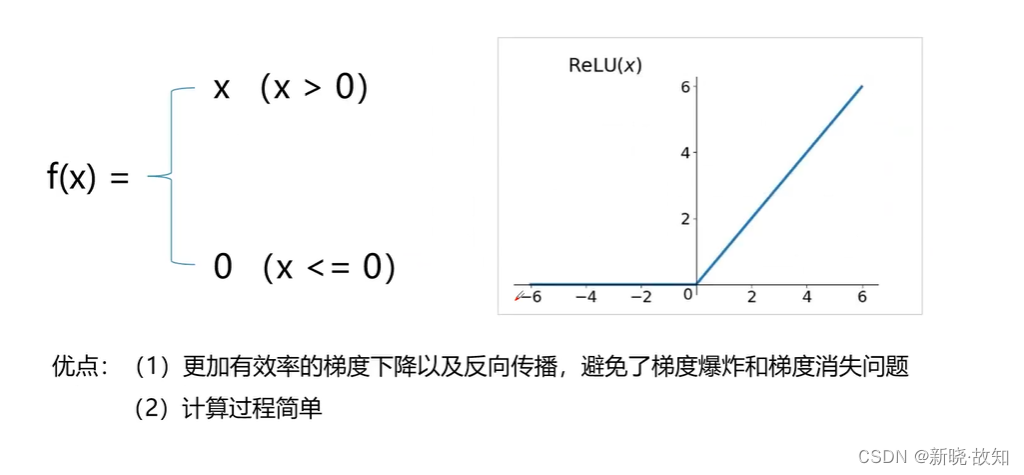
在这里插入图片描述
常用的激活函数——ReLU（修正线性单元）函数：
在这里插入图片描述
常用的激活函数——Softmax函数：
在这里插入图片描述
总结：在这里插入图片描述

三、损失函数与梯度下降

1.损失函数

1.1什么是损失函数

在这里插入图片描述

1.2损失函数的作用

在这里插入图片描述

1.3常用的损失函数

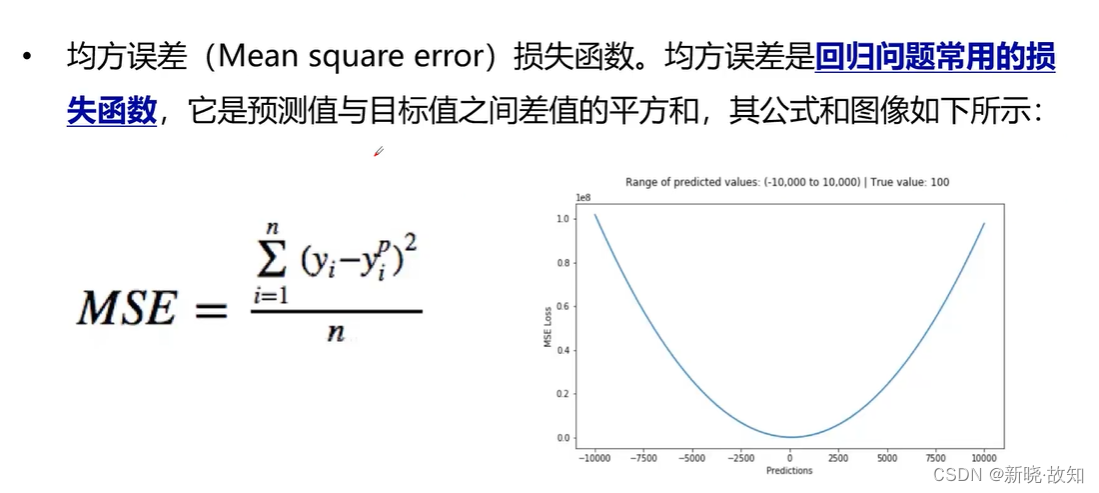
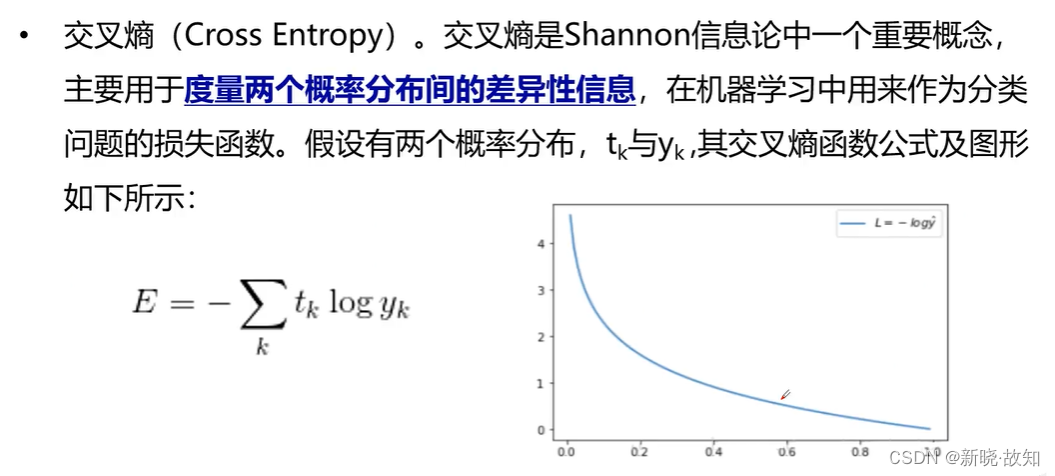
在这里插入图片描述
在这里插入图片描述

2.梯度下降

2.1什么是梯度

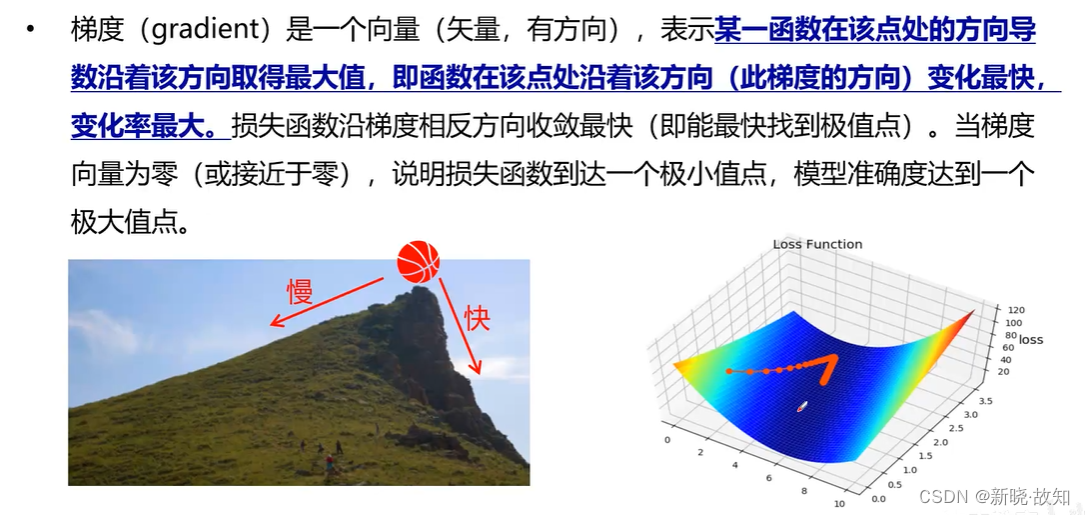
在这里插入图片描述

2.2梯度下降

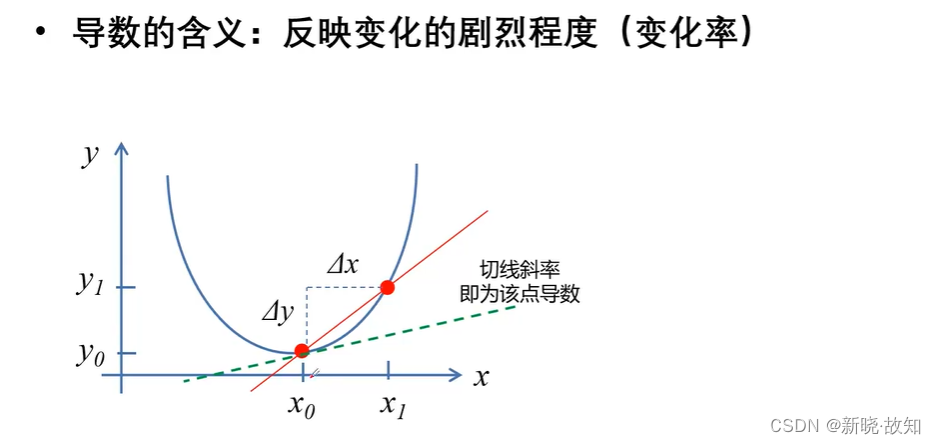
在这里插入图片描述
梯度下降计算：
依赖于导数、偏导数：
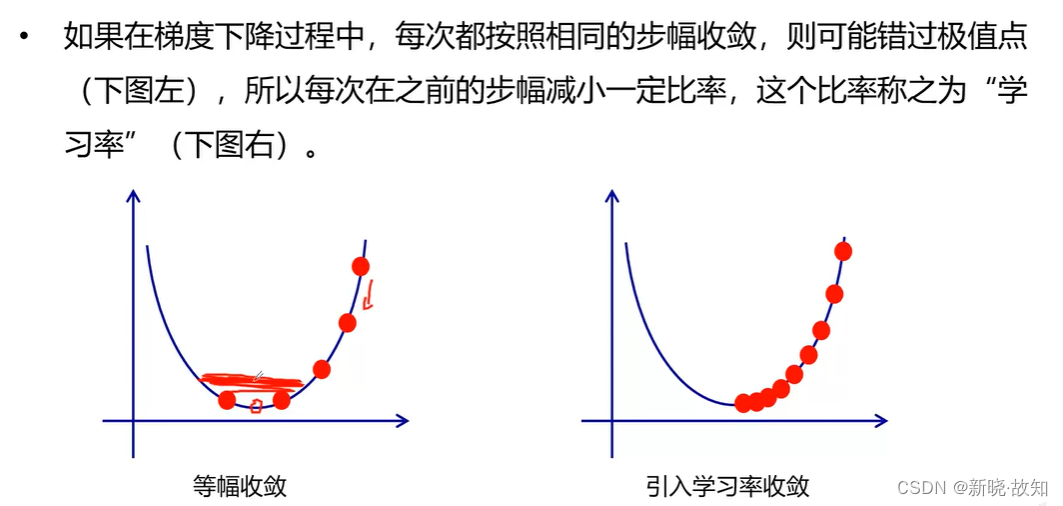
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.3学习率

在这里插入图片描述

2.4梯度递减训练法则

在这里插入图片描述

2.5梯度下降算法

批量梯度下降:
在这里插入图片描述
随机梯度下降：
在这里插入图片描述
小批量梯度下降：
在这里插入图片描述

2.6几种梯度下降算法收敛比较

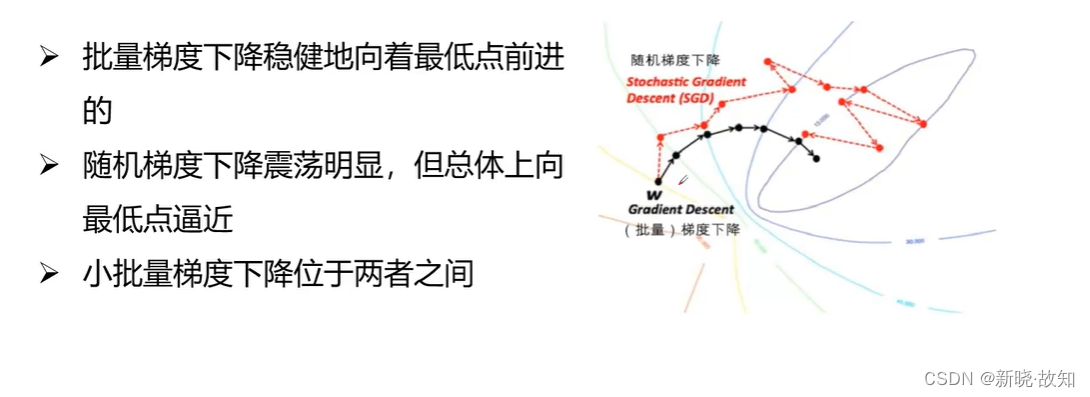
在这里插入图片描述
总结:
在这里插入图片描述

四、反向传播算法

1.什么是正向传播网络

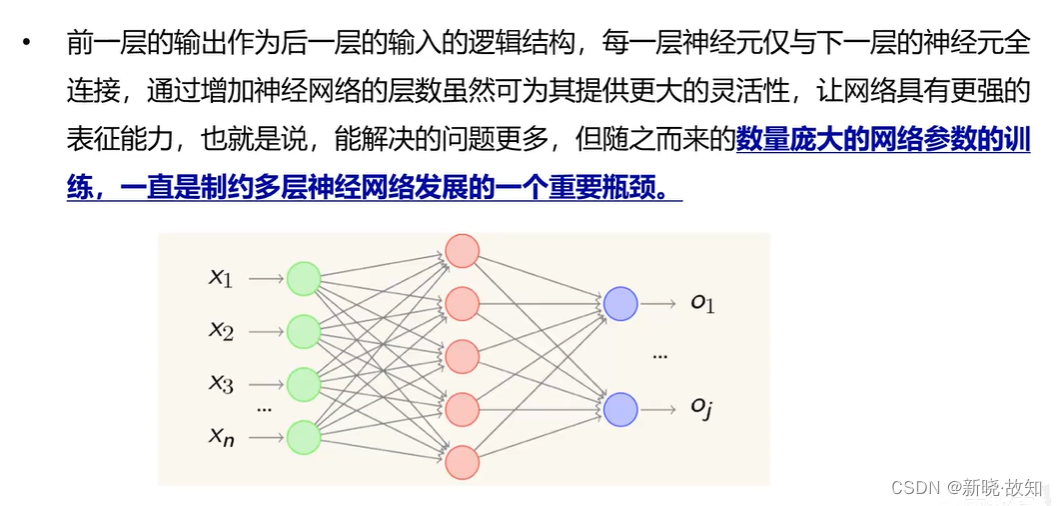
在这里插入图片描述

2.什么是反向传播网络

在这里插入图片描述

2.1为什么需要反向传播

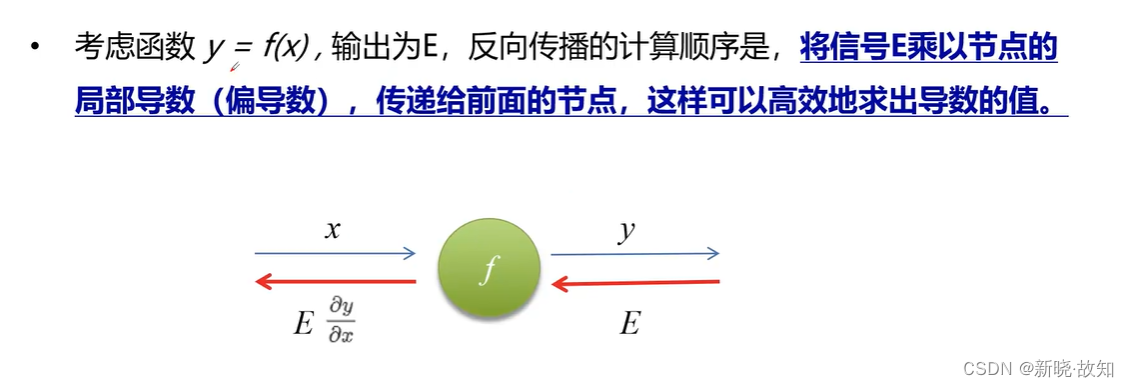
在这里插入图片描述
图解反向传播：
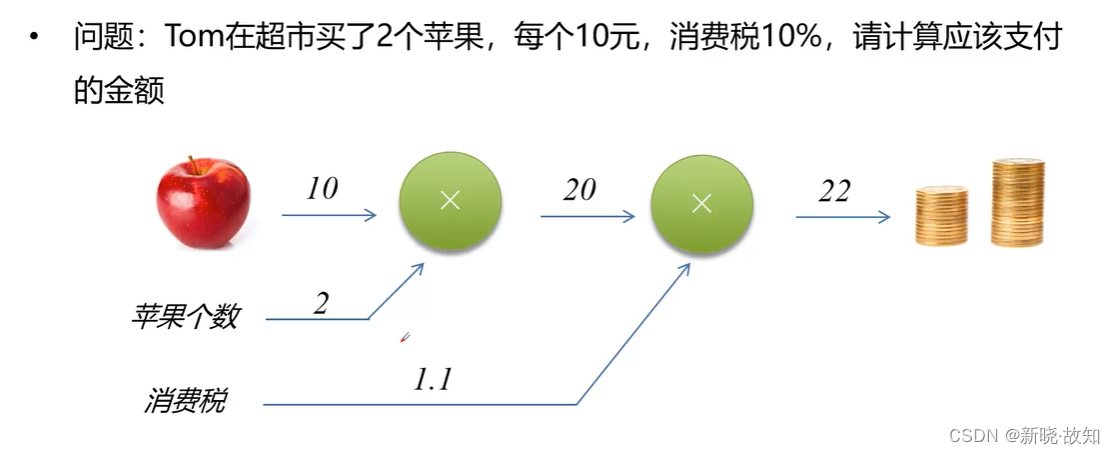
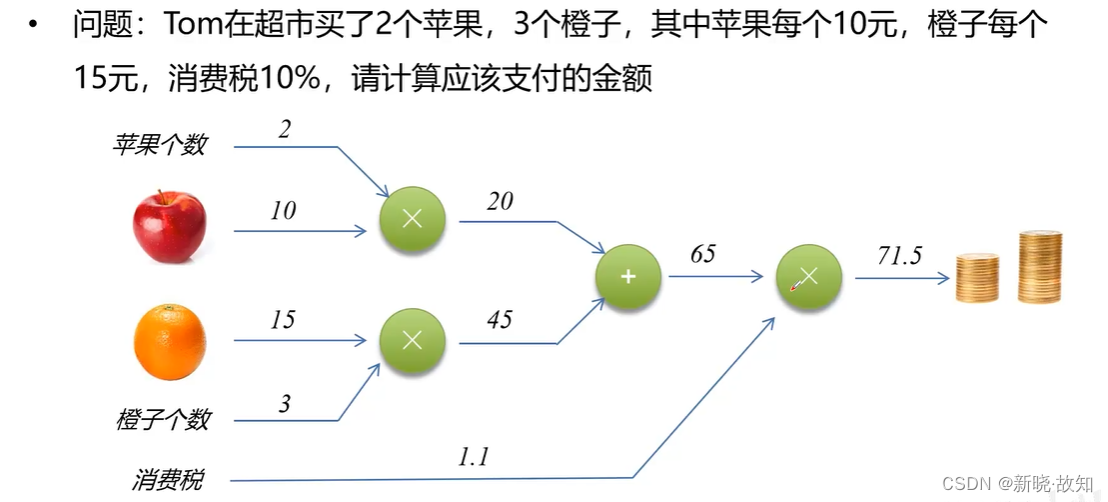
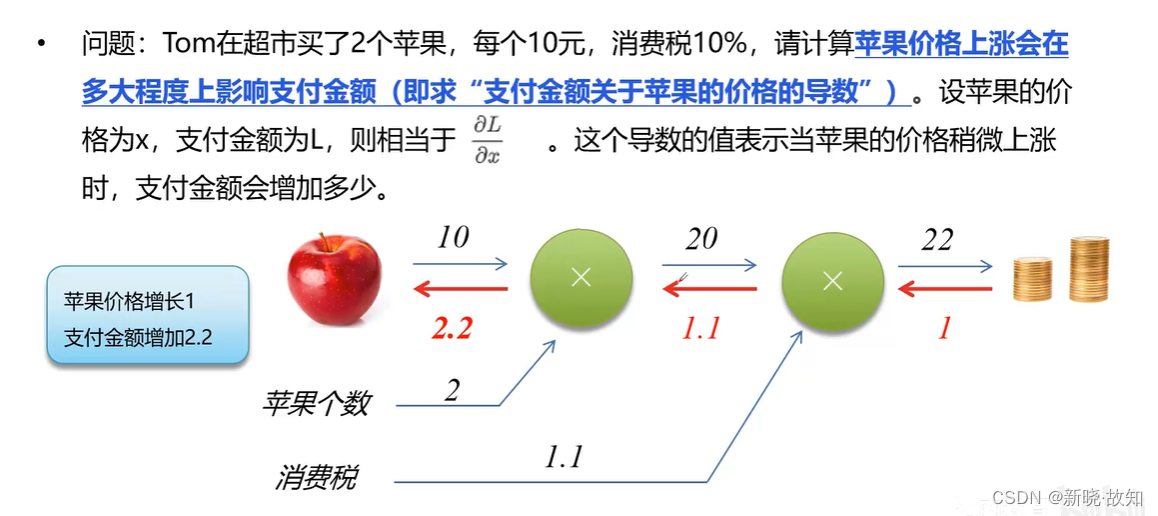
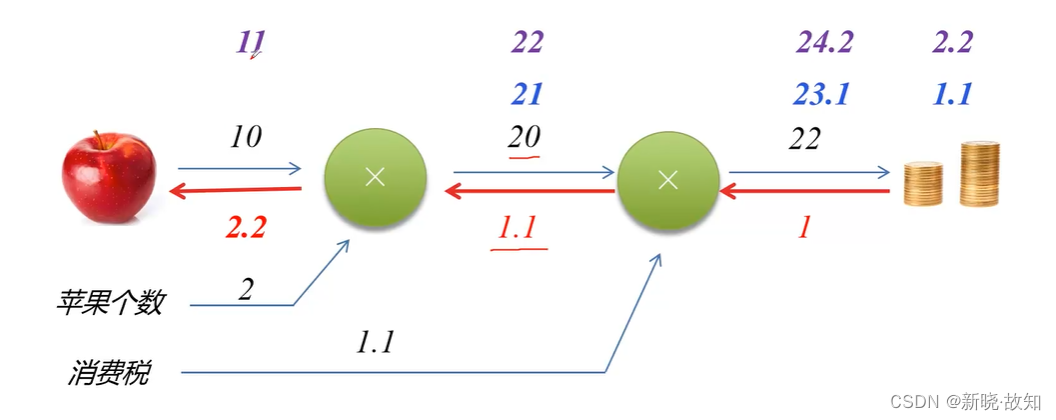
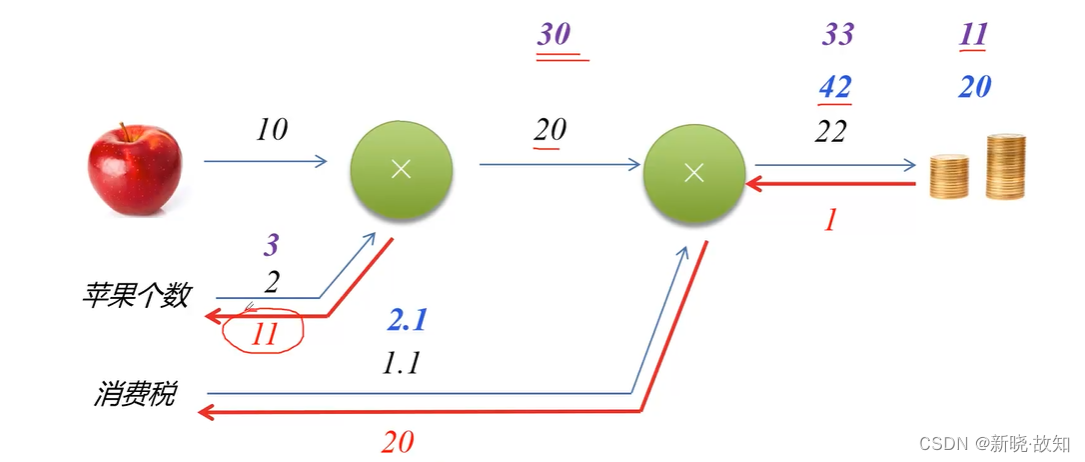
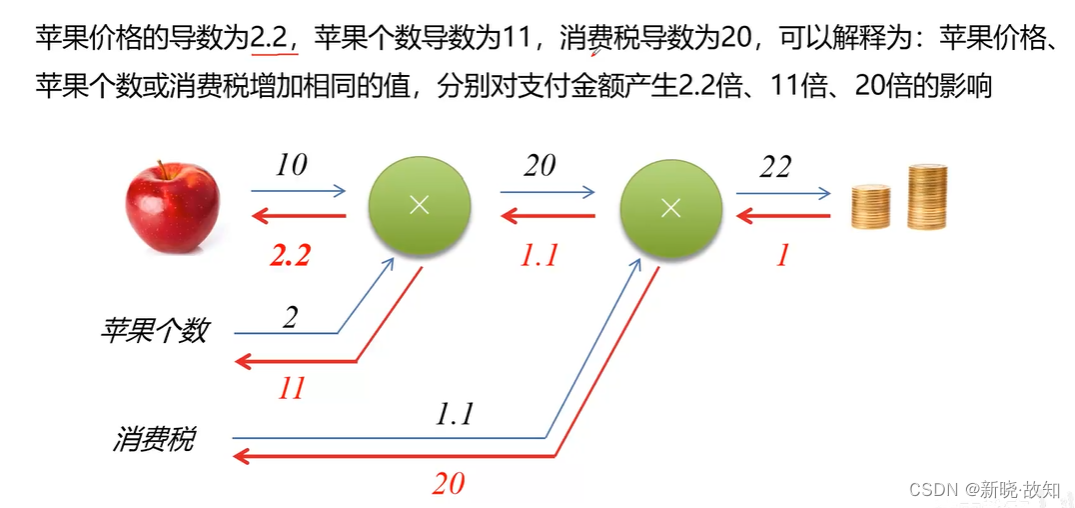
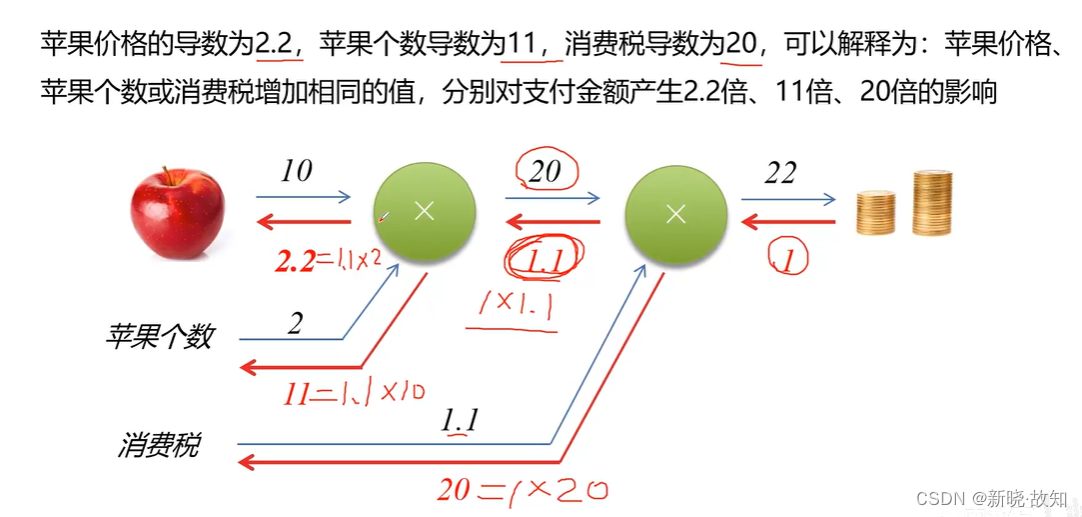
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.2反向传播计算

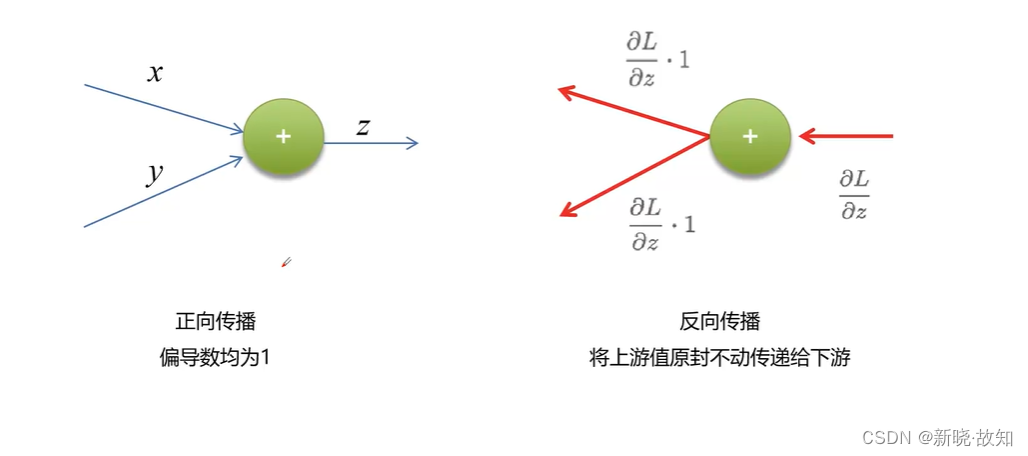
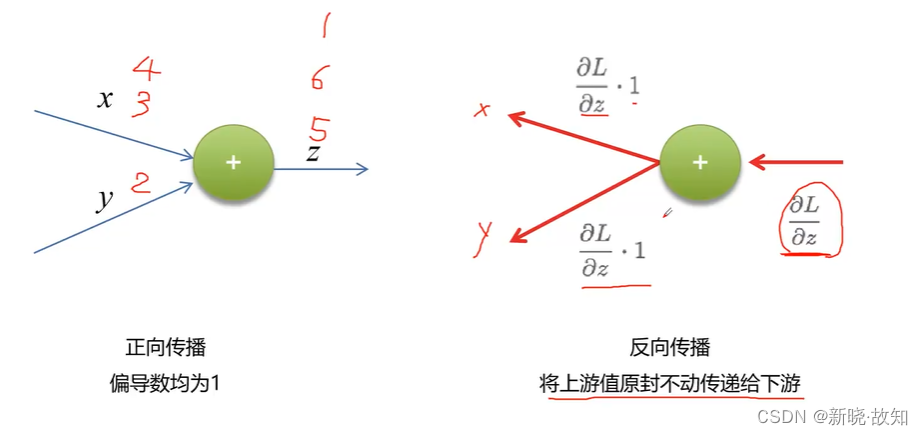
在这里插入图片描述
加法节点反向传播计算：
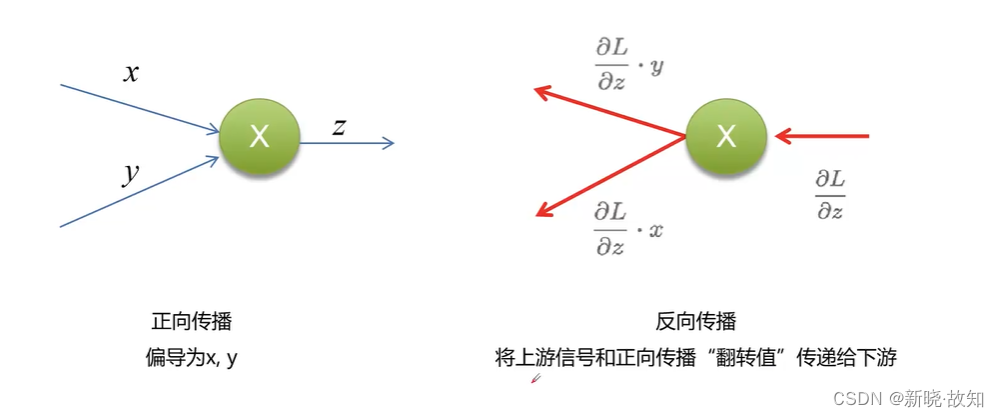
在这里插入图片描述
在这里插入图片描述

乘法节点反向传播计算：
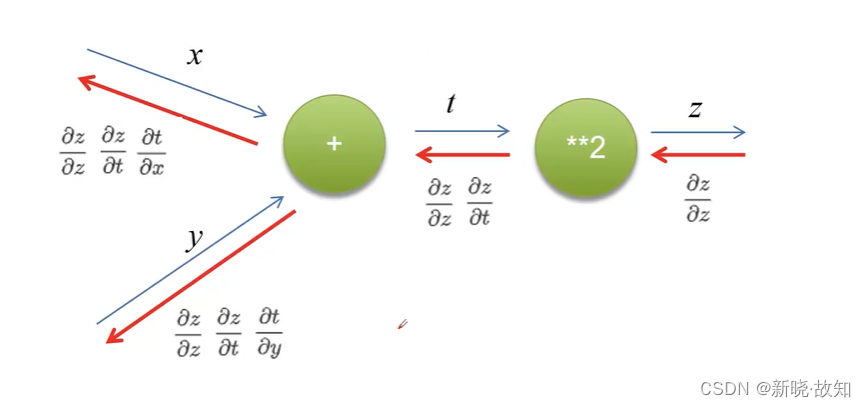
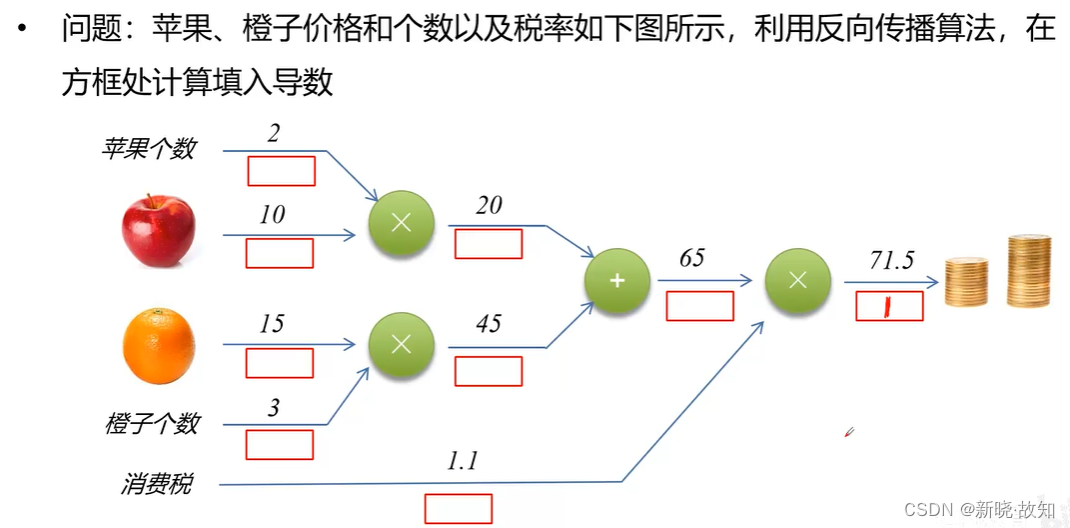
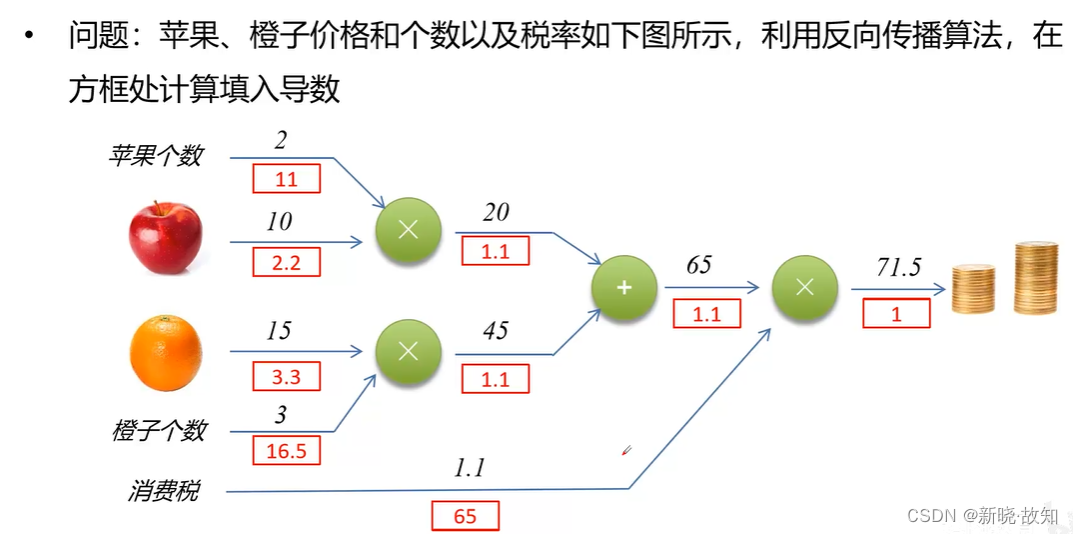
在这里插入图片描述
链式求导法则：
在这里插入图片描述
在这里插入图片描述
练习：
在这里插入图片描述
在这里插入图片描述

五、卷积神经网络

1.什么是卷积

在这里插入图片描述
离散卷积与多维卷积：
在这里插入图片描述
生活中的卷积：
在这里插入图片描述

2. 卷积神经网络

2.1全连接神经网络的局限

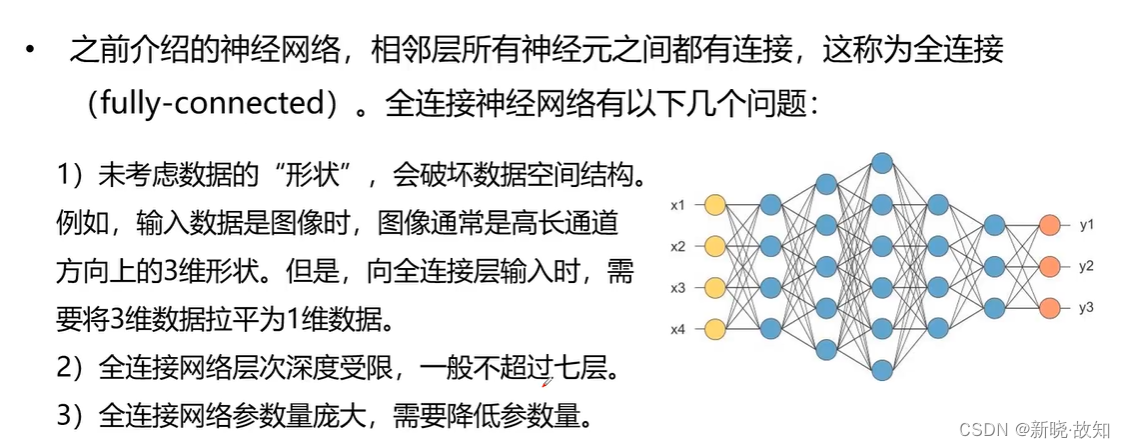
在这里插入图片描述

2.2什么是卷积神经网络

在这里插入图片描述
在这里插入图片描述

2.3卷积运算

单通道、二维卷积：
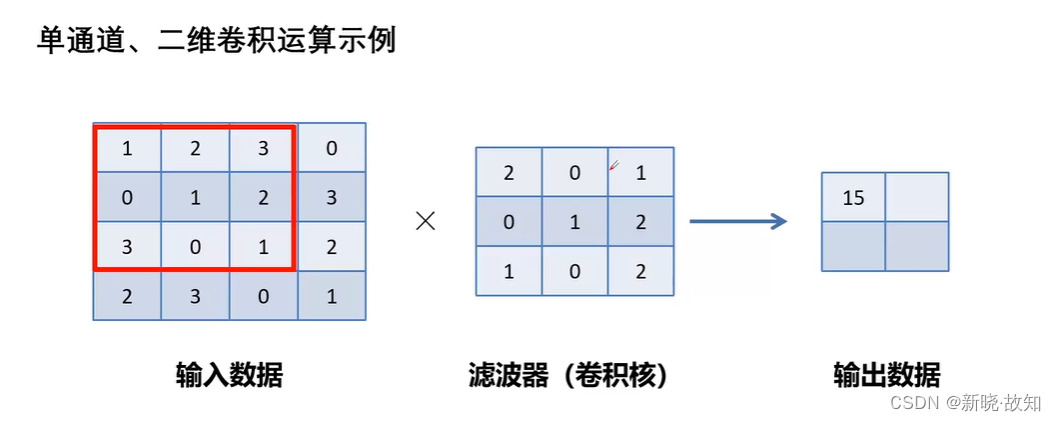
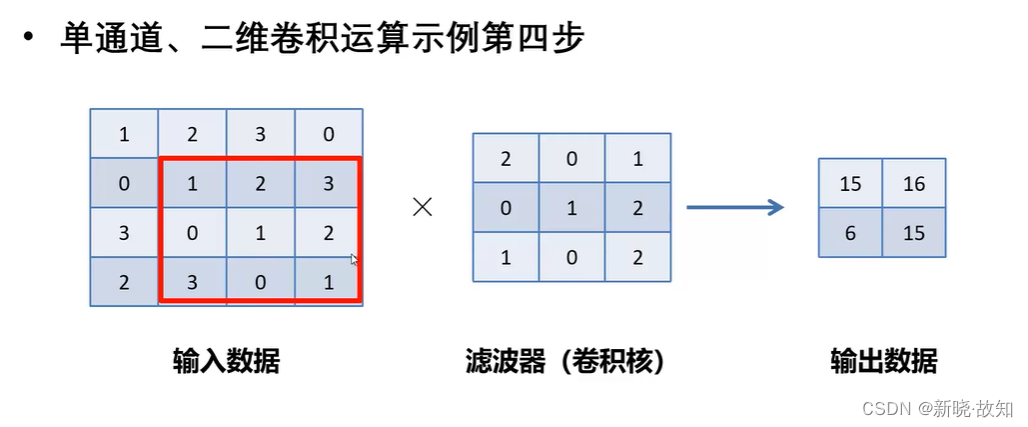
在这里插入图片描述在这里插入图片描述
带填充的卷积运算：
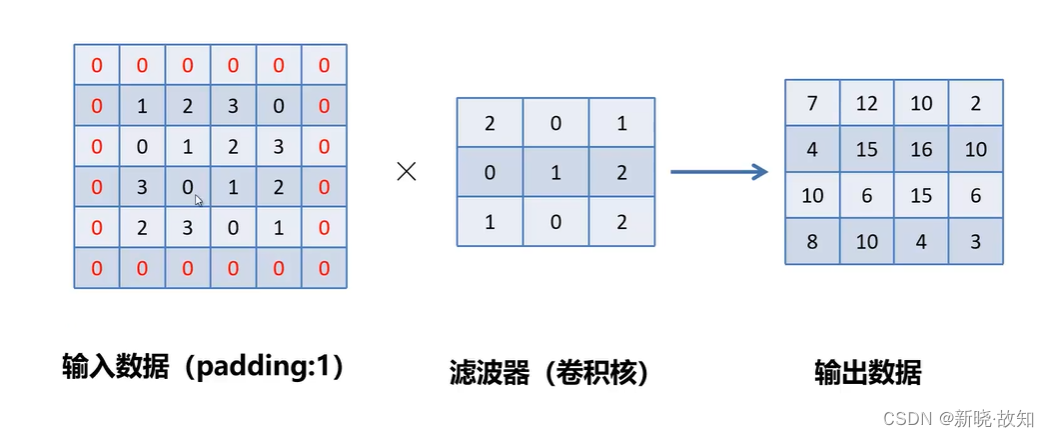
在这里插入图片描述

步符为2的卷积运算：
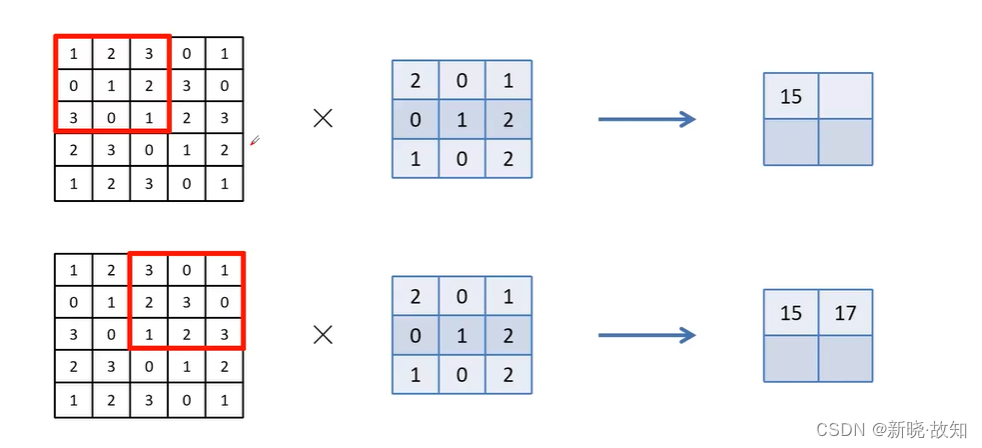
在这里插入图片描述
输入输出大小计算公式：
在这里插入图片描述
多通道卷积计算演示GIF:
卷积计算演示GIF
卷积运算的效果:
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.4使用Python模拟实现卷积运算

# img_conv.py
# 图像卷积示例
from scipy import signal
from scipy import misc
import matplotlib.pyplot as plt
import numpy as np
import scipy.ndimage as sn

im = misc.imread("d:\\tmp\\lily.png", flatten=True)  
# im = sn.imread("d:\\tmp\\lily.png", flatten=True)
#1.以上两种读取函数均可以读取图像，返回的是矩阵数据
#2."d:\\tmp\\lily.png"这个是图片存储的路径

flt = np.array([[-1, 0, 1],
                [-2, 0, 2],
                [-1, 0, 1]])  # 卷积核(过滤器)
flt2 = np.array([[1, 2, 1],
                 [0, 0, 0],
                 [-1, -2, -1]]) # 另一个卷积核(对垂直方向上的色彩变化敏感)
grad = signal.convolve2d(im,  # 输入数据
                         flt,  # 卷积核
                         boundary="symm",  # 边沿处理方式
                         mode="same").astype("int32")  # same表示同维卷积
grad2 = signal.convolve2d(im,  # 输入数据
                        flt2,  # 卷积核
                         boundary="symm",  # 边沿处理方式
                         mode="same").astype("int32")  # same表示同维卷积
# 可视化
plt.figure("Conv2D")
plt.subplot(131)  # 第一个子图, 显示原图
plt.imshow(im, cmap="gray")  # 显示原图
plt.xticks([])
plt.yticks([])

plt.subplot(132)  # 第二个子图, 显示卷积后的图像
plt.imshow(grad, cmap="gray")  # 显示卷积后的图像
plt.xticks([])
plt.yticks([])

plt.subplot(133)  # 第三个子图, 显示flt2卷积后的图像
plt.imshow(grad2, cmap="gray")  # 显示flt2卷积后的图像
plt.xticks([])
plt.yticks([])
plt.show()

在这里插入图片描述
卷积计算后：
在这里插入图片描述

四、经典卷积网络介绍

1.卷积神经网络结构

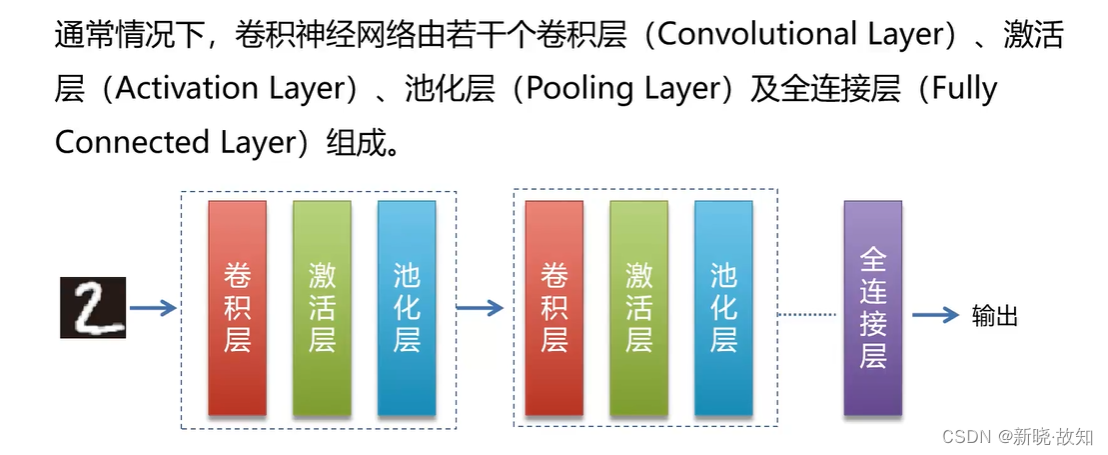
在这里插入图片描述

1.1卷积层

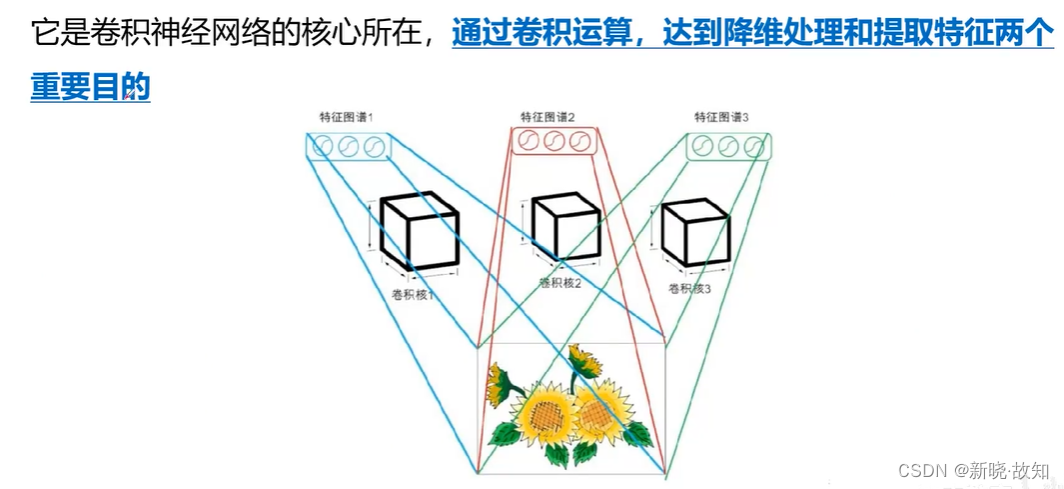
在这里插入图片描述

1.2激活层

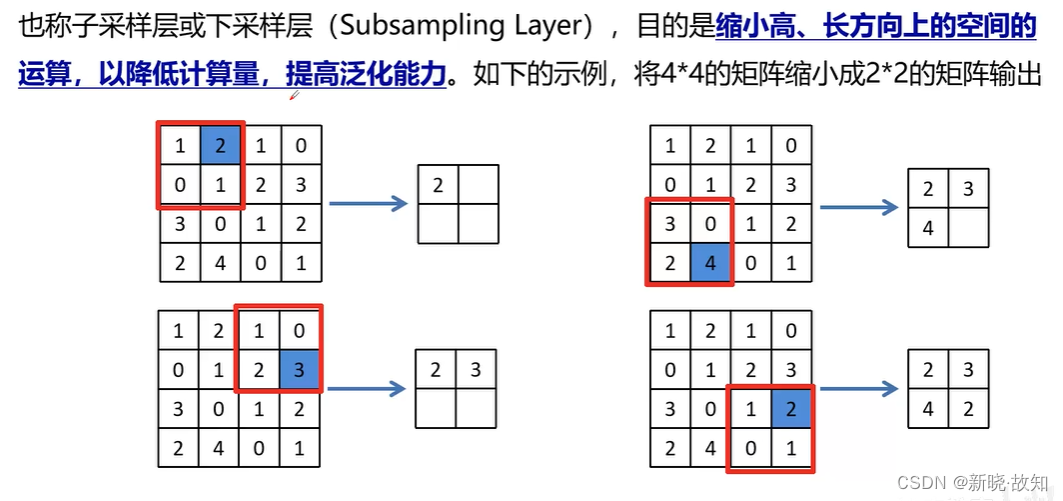
在这里插入图片描述

1.3池化层

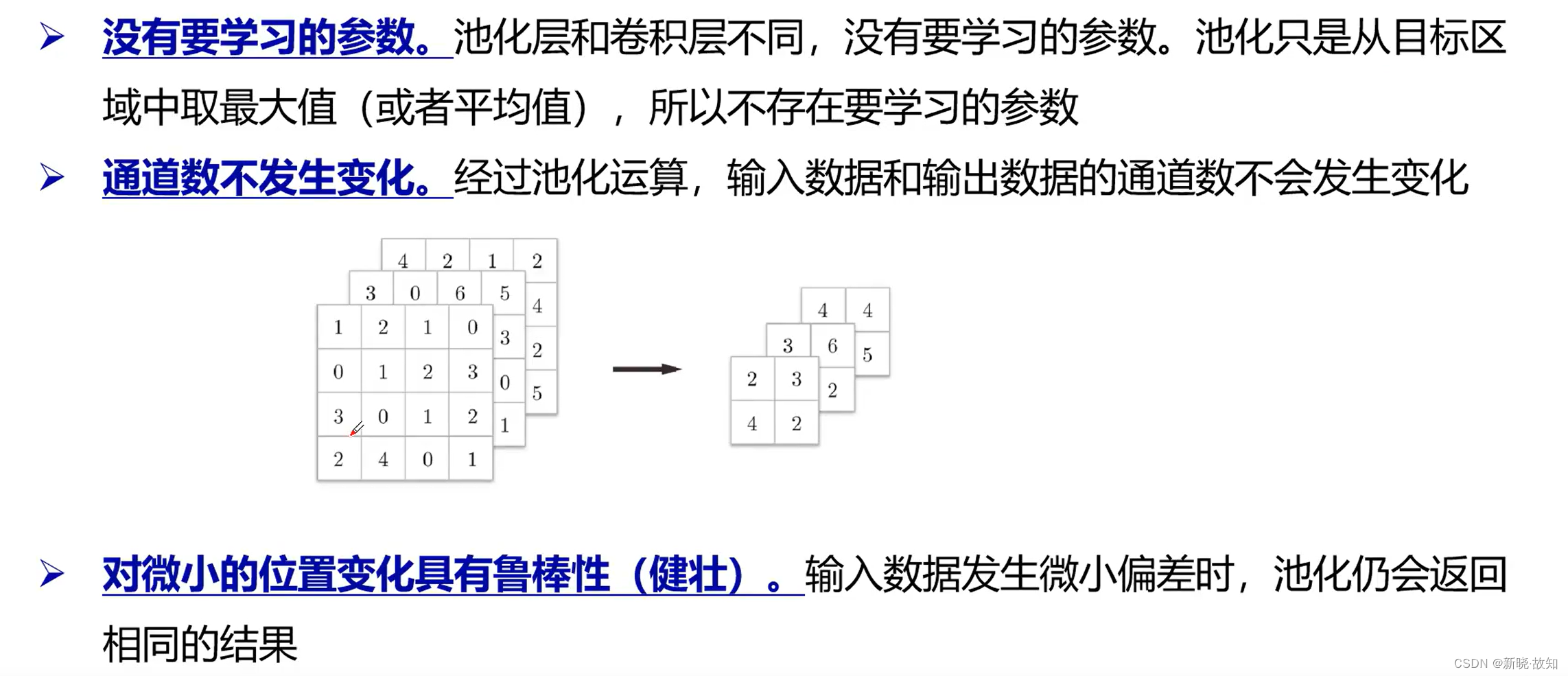
在这里插入图片描述
在这里插入图片描述
池化层的特征：
在这里插入图片描述

1.4全连接层

在这里插入图片描述

2.经典卷积神经网络模型

2.1LeNet

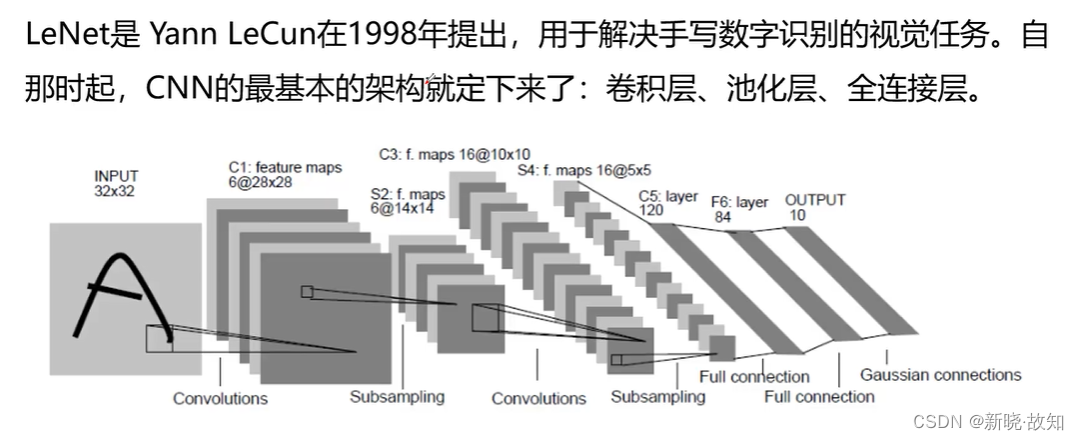
在这里插入图片描述
在这里插入图片描述

2.2AlexNet

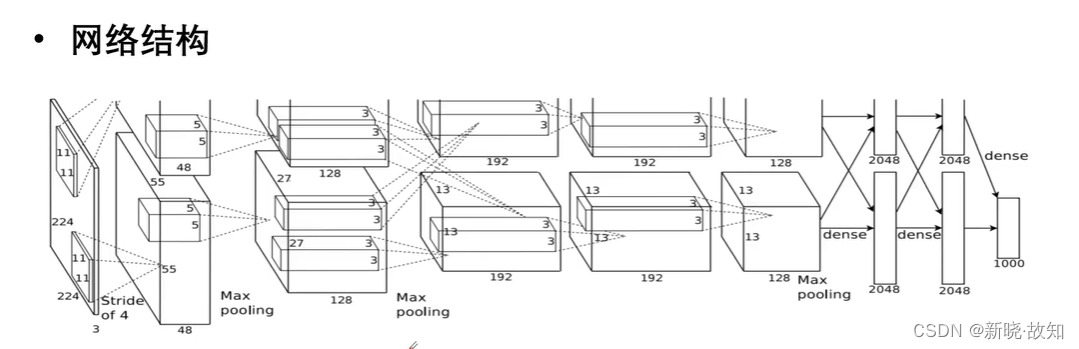
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
AlexNet参考论文地址链接：http://www.cs.toronto.edu/~fritz/absps/imagenet.pdf

2.3VGG

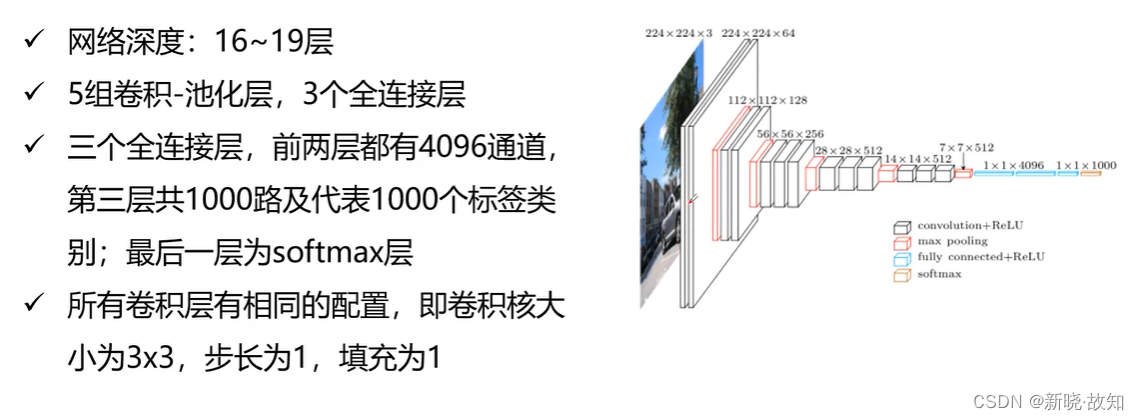
在这里插入图片描述
在这里插入图片描述
总结：
在这里插入图片描述

后记：
●本博客基于B站开源学习资源，是作者学习的笔记记录，仅用于学习交流，不做任何商业用途！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1552792.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

AugmentedReality之路-显示隐藏AR坐标原点（3）

AugmentedReality之路-显示隐藏AR坐标原点（3）

本文介绍如何显示/隐藏坐标原点&#xff0c;分析AR坐标原点跟手机的位置关系 1、AR坐标原点在哪里 当我们通过AugmentedReality的StartARSession函数打开AR相机的那一刻&#xff0c;相机所在的位置就是坐标原点。 2、创建指示箭头资产 1.在Content/Arrow目录创建1个Actor类…
阅读更多...
NanoMQ的安装与部署

NanoMQ的安装与部署

本文使用docker进行安装&#xff0c;因此安装之前需要已经安装了docker 拉取镜像 docker pull emqx/nanomq:latest 相关配置及密码认证 创建目录/usr/local/nanomq/conf以及配置文件nanomq.conf、pwd.conf # # # # MQTT Broker # # mqtt {property_size 32max_packet_siz…
阅读更多...
|行业洞察·趋势报告|《2024旅游度假市场简析报告-17页》

|行业洞察·趋势报告|《2024旅游度假市场简析报告-17页》

报告的主要内容解读&#xff1a; 居民收入提高推动旅游业发展&#xff1a;报告指出&#xff0c;随着人均GDP的提升&#xff0c;居民的消费能力增强&#xff0c;旅游需求从传统的观光游向休闲、度假游转变&#xff0c;国内人均旅游消费持续增加。 政府政策促进旅游市场复苏&…
阅读更多...
对象内存布局

对象内存布局

对象头 对象标记Mark Word 所以New一个对象 没有其他信息 就是16字节 Object obj = new Object();
阅读更多...
设计模式之原型模式讲解

设计模式之原型模式讲解

原型模式本身就是一种很简单的模式&#xff0c;在Java当中&#xff0c;由于内置了Cloneable 接口&#xff0c;就使得原型模式在Java中的实现变得非常简单。UML图如下&#xff1a; 我们来举一个生成新员工的例子来帮助大家理解。 import java.util.Date; public class Employee…
阅读更多...
Git--08--Git分支合并操作

Git--08--Git分支合并操作

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 Git分支合并操作案例流程客户端&#xff1a;GitExtensions操作步骤&#xff1a;A操作步骤&#xff1a;B操作步骤&#xff1a;C操作步骤&#xff1a;D操作步骤&#…
阅读更多...
Ubuntu20.04安装OpenCV并在vsCode中配置

Ubuntu20.04安装OpenCV并在vsCode中配置

1. 安装OpenCV 1.1 安装准备&#xff1a; 1.1.1 安装cmake sudo apt-get install cmake 1.1.2 依赖环境 sudo apt-get install build-essential libgtk2.0-dev libavcodec-dev libavformat-dev libjpeg-dev libswscale-dev libtiff5-dev sudo apt-get install libgtk2.0-d…
阅读更多...
opencv如何利用掩码将两张图合成一张图

opencv如何利用掩码将两张图合成一张图

最近在学opencv&#xff0c; 初学者。 里面有提到如何将两张图合成一张图&#xff0c; 提供了两个方法 一种是直接通过图片透明度权重进行融合 img1 cv.imread(ml.png) img2 cv.imread(opencv-logo.png) dst cv.addWeighted(img1,0.7,img2,0.3,0) cv.imshow(dst,dst) cv.…
阅读更多...
iOS —— 初识KVO

iOS —— 初识KVO

iOS —— 初始KVO KVO的基础1. KVO概念2. KVO使用步骤注册KVO监听实现KVO监听销毁KVO监听 3. KVO基本用法4. KVO传值禁止KVO的方法 注意事项&#xff1a; KVO的基础 1. KVO概念 KVO是一种开发模式&#xff0c;它的全称是Key-Value Observing (观察者模式) 是苹果Fundation框架…
阅读更多...
MySQL ② —— 索引原理

MySQL ② —— 索引原理

1. 索引 1.1 分类 主键索引、唯一索引、普通索引、组合索引、以及全文索引 主键索引 非空唯一索引&#xff0c;一个表只有一个主键索引&#xff1b;在 innodb 中&#xff0c;主键索引的 B 树包含表数据信息。 唯一索引 不可以出现相同的值&#xff0c;可以有 NULL 值。 …
阅读更多...
3.28学习总结

3.28学习总结

java 封装 封装体现了java的面向对象的特点,用户不用知道程序是如何运行的,只用按照所给的格式输入参数,便可得到对应的结果. 一个完整的封装需要每个实例变量都用private来修饰并拥有相应的public getter和setter方法. 代码 public class girl {private int age;public st…
阅读更多...
TABLE使用篇之奇门异术

TABLE使用篇之奇门异术

table使用时候有时候会有下面界面 hover提示框&#xff0c;用element的el-popover可以显示该操作&#xff0c;但是会发现 取消操作的时候&#xff0c;el-popover不会自动消失&#xff0c;虽然失去焦点改框会自动消失&#xff0c;但是看起来对用户不是很友好 解决办法&#xff…
阅读更多...
CDH集群hive初始化元数据库失败

CDH集群hive初始化元数据库失败

oracle数据库操作&#xff1a; 报错如下&#xff1a;命令 (Validate Hive Metastore schema (237)) 已失败 截图如下&#xff1a; 后台日志部分摘录&#xff1a; WARNING: Use “yarn jar” to launch YARN applications. SLF4J: Class path contains multiple SLF4J binding…
阅读更多...
Vite 为什么比 Webpack 快？

Vite 为什么比 Webpack 快？

目录 1. Webpack 的构建原理 2. Script 的模块化&#xff08;主流浏览器对 ES Modules 的支持&#xff09; 3. Webpack vs Vite 开发模式的差异 对 ES Modules 的支持 底层语言的差异 热更新的处理 1. Webpack 的构建原理 前端之所以需要类似于 Webpack 这样的构建工具&…
阅读更多...
vue纯前端过滤嵌套数据，通过关键字搜索过滤嵌套数据

vue纯前端过滤嵌套数据，通过关键字搜索过滤嵌套数据

1.过滤效果&#xff1a; 2. cardList 数据源&#xff1a; [ { "id": 4, "createTime": "2024-03-28 02:47:18", "updateTime": "2024-03-28 02:47:18", "uniqueId": "…
阅读更多...
前端学习-CSS基础-Day3

前端学习-CSS基础-Day3

一、CSS三大特性 1.1层叠性 相同选择器给设置相同的样式&#xff0c;此时一个样式就会覆盖&#xff08;层叠&#xff09;另一个冲突的样式。层叠性主要解决样式冲突的问题 层叠性原则&#xff1a; 1.样式冲突&#xff0c;遵循的原则是就近原则&#xff0c;哪个样式离结构近&a…
阅读更多...
React系列之合成事件与事件处理机制

React系列之合成事件与事件处理机制

文章目录 React事件处理机制原生事件的事件机制事件代理&#xff08;事件委托&#xff09; 合成事件使用合成事件目的合成事件原生事件区别事件池 原生事件和React事件的执行顺序e.stopPropagation() React17事件机制的修改 React事件处理机制 react 事件机制基本理解&#xf…
阅读更多...
Maven配置国内镜像-阿里云仓库镜像

Maven配置国内镜像-阿里云仓库镜像

使用自己安装maven环境时&#xff1a; 打开解压目录下conf/settings.xml文件 使用Idea自带的Maven时&#xff1a; 打开Idea安装路径\plugins\maven\lib\maven3\conf\settings.xml文件 在mirrors节点中加入如下配置&#xff1a; <!-- 加入如下mirror节点 使用国内阿里云仓…
阅读更多...
fastadmin学习05-开启debug以及配置

fastadmin学习05-开启debug以及配置

FastAdmin 框架提供了对 .env 环境变量配置的支持&#xff0c;并附带一个默认示例文件 .env.sample。在安装后&#xff0c;框架并不会自动启用 env 环境变量&#xff0c;需要手动将 .env.sample 复制为 .env 并进行配置。 如果不开启.env会读取database.php中的配置 下面测试…
阅读更多...
鸿蒙OS开发实例：【页面传值跳转】

鸿蒙OS开发实例：【页面传值跳转】

介绍 本篇主要介绍如何在HarmonyOS中&#xff0c;在页面跳转之间如何传值 HarmonyOS 的页面指的是带有Entry装饰器的文件&#xff0c;其不能独自存在&#xff0c;必须依赖UIAbility这样的组件容器 如下是官方关于State模型开发模式下的应用包结构示意图&#xff0c;Page就是…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023