目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2021年,B Abdollahzadeh等人受到大猩猩社会行为启发,提出了人工大猩猩部队优化算法(Artificial Gorilla Troops Optimizer, GTO)。
2.算法原理
2.1算法思想
GTO模拟了大猩猩的种群迁移和求偶行为:
- 探索阶段:种群迁移包括已知位置、未知位置和同伴位置三种
- 开发阶段:求偶行为模拟了雄性大猩猩争夺雌性的行为
2.2算法过程
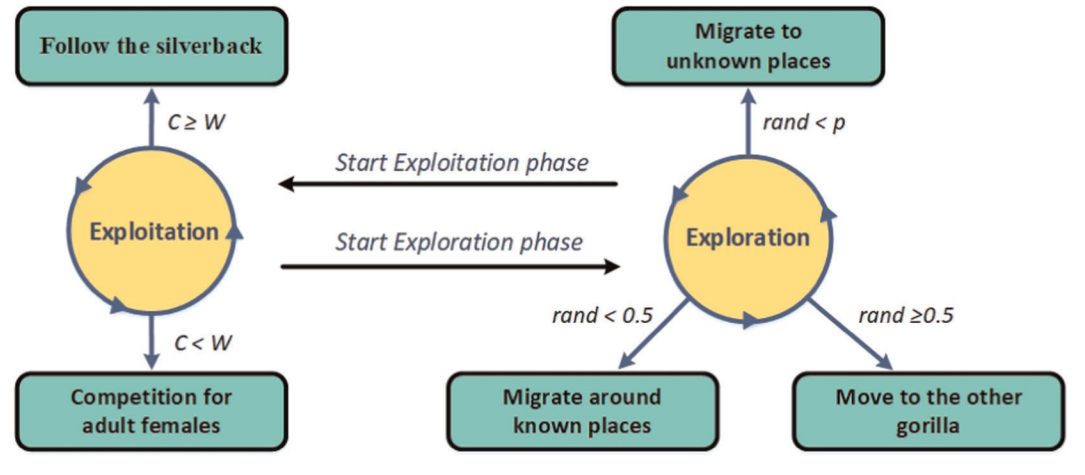
探索阶段:
GTO算法包括三种探索机制,对应大猩猩的三种迁移位置。当随机数小于概率阈值 p(0.03) 时,大猩猩向未知地点迁移;当随机数小于0.5时,大猩猩向已知地点迁移;当随机数大于或等于0.5时,大猩猩向同伴迁移。
G
X
(
t
)
=
{
(
U
B
−
L
B
)
×
r
1
+
L
B
,
rand
<
p
(
r
2
−
C
)
×
X
n
(
t
)
+
L
×
H
,
rand
<
p
X
(
t
)
−
L
×
(
L
×
(
X
(
t
)
−
G
X
n
(
t
)
)
+
r
3
×
(
X
(
t
)
−
G
X
n
(
t
)
)
)
,
rand
<
0.5
(1)
\mathrm{GX}(t)=\begin{cases}(\mathrm{UB-LB})\times r_1+\mathrm{LB},&\text{rand}<p\\(r_2-C) \times X_n(t)+L\times H,&\text{rand}<p\\X(t)-L\times(L\times(X(t)-\mathrm{GX}_n(t))+r_3\times(X(t)-\mathrm{GX}_n(t))),&\text{rand}<0.5\end{cases}\tag{1}
GX(t)=⎩
⎨
⎧(UB−LB)×r1+LB,(r2−C)×Xn(t)+L×H,X(t)−L×(L×(X(t)−GXn(t))+r3×(X(t)−GXn(t))),rand<prand<prand<0.5(1)
Xr 表示上一代种群中任意大猩猩的最优位置,X 表示上一代大猩猩的最优位置,GX 表示当前大猩猩的位置,GXr表示当前种群中任意大猩猩的位置,t 表示大猩猩个体,参数 C、L、H表述为:
C
=
F
×
(
1
−
I
t
M
a
x
I
t
)
L
=
C
×
l
H
=
Z
×
X
(
t
)
F
=
cos
(
2
×
r
4
)
+
1
Z
∈
[
−
C
,
C
]
(2)
\begin{gathered} C=F\times\left(1-\frac{\mathrm{It}}{\mathrm{Max}\mathrm{It}}\right) \\ L=C\times l \\ H=Z\times X(t) \\ F=\cos(2\times r_{4})+1 \\ Z \in [- C,C] \end{gathered}\tag{2}
C=F×(1−MaxItIt)L=C×lH=Z×X(t)F=cos(2×r4)+1Z∈[−C,C](2)
开发阶段:
当 C≥W 时,表示种群跟随银背大猩猩迁移:
G
X
(
t
)
=
L
×
M
×
(
X
(
t
)
−
X
b
)
+
X
(
t
)
M
=
(
∣
1
N
∑
i
=
1
N
G
X
i
(
t
)
∣
g
)
1
g
g
=
2
L
(3)
\begin{aligned}\mathrm{GX}(t)&=L\times M\times(X(t)-X_b)+X(t)\\M&=\Big(\left.\left|\frac1N\sum_{i=1}^N\mathrm{GX}_i(t)\right|^g\right)^{\frac1g}\\g&=2^L\end{aligned}\tag{3}
GX(t)Mg=L×M×(X(t)−Xb)+X(t)=(
N1i=1∑NGXi(t)
g)g1=2L(3)
当 C<W 时,表示雄性大猩猩求偶行为:
G
X
(
t
)
=
X
b
−
(
X
b
×
Q
−
X
(
t
)
×
Q
)
×
A
(4)
\mathrm{GX}(t)=X_b-(X_b\times Q-X(t)\times Q)\times A\tag{4}
GX(t)=Xb−(Xb×Q−X(t)×Q)×A(4)
参数 Q 用来模拟冲击力,参数 A 用来模拟暴力程度:
Q
=
2
×
r
5
−
1
A
=
β
×
E
E
=
{
r
a
n
d
n
(
1
,
d
)
,
r
a
n
d
⩾
0.5
r
a
n
d
n
(
1
,
1
)
,
r
a
n
d
<
0.5
(5)
\begin{gathered} Q=2\times r_{5}-1 \\ A=\beta\times E \\ \left.E=\left\{\begin{matrix}{\mathrm{randn}(1,d),}&{\mathrm{rand}\geqslant0.5}\\{\mathrm{randn}(1,1),}&{\mathrm{rand}<0.5}\\\end{matrix}\right.\right. \end{gathered}\tag{5}
Q=2×r5−1A=β×EE={randn(1,d),randn(1,1),rand⩾0.5rand<0.5(5)
伪代码:

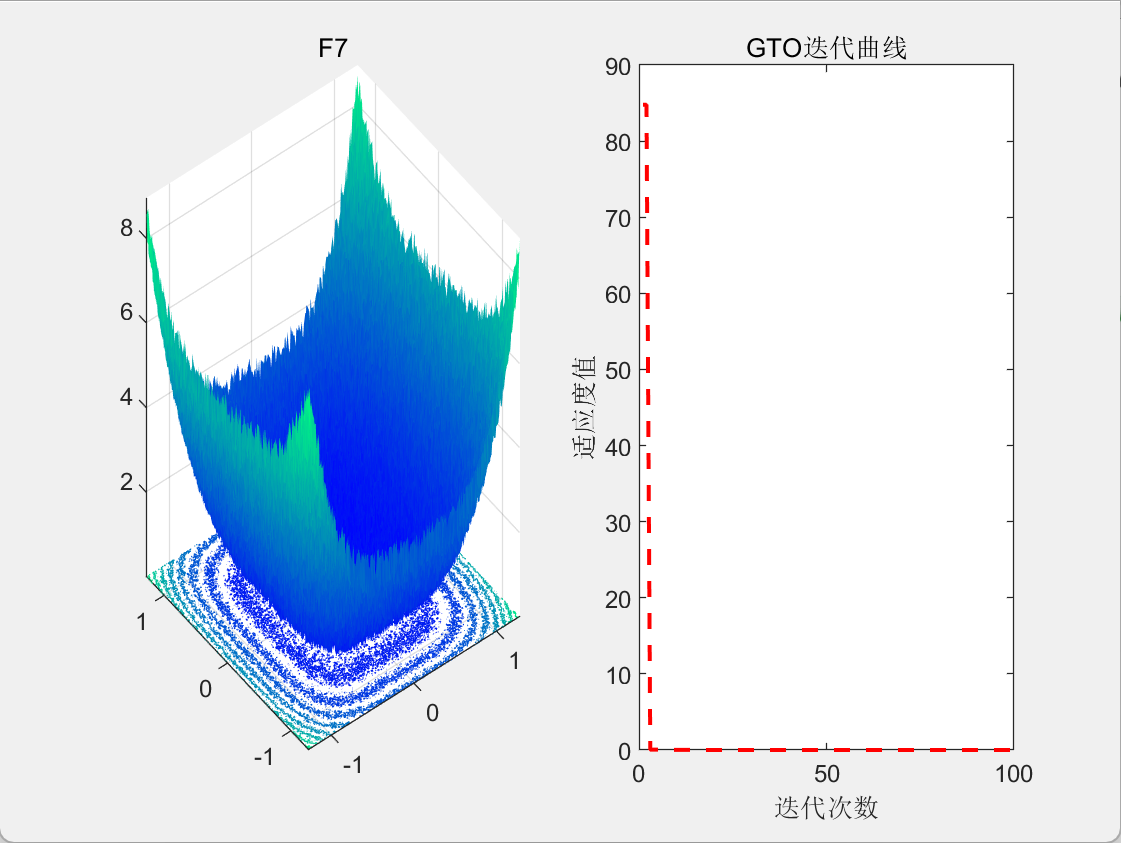
3.结果展示
4.参考文献
[1] Abdollahzadeh B, Soleimanian Gharehchopogh F, Mirjalili S. Artificial gorilla troops optimizer: a new nature‐inspired metaheuristic algorithm for global optimization problems[J]. International Journal of Intelligent Systems, 2021, 36(10): 5887-5958.