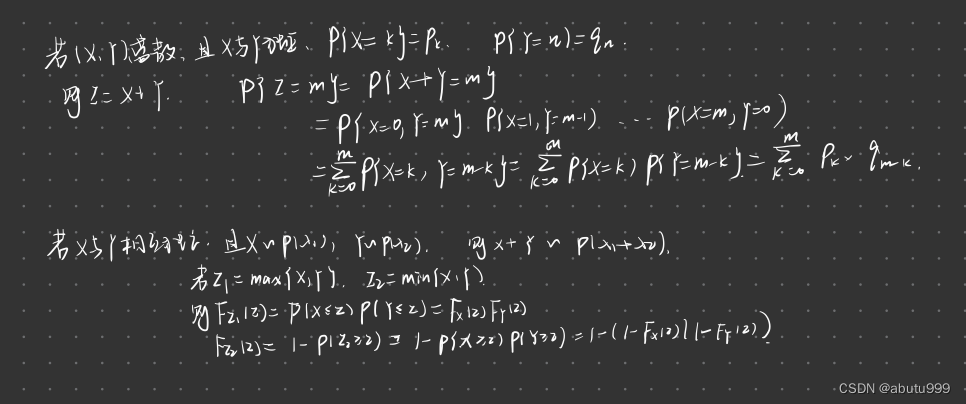随机变量与分布函数

随机变量

随机变量：一个随机变量是对随机现象可能的结果的一种数学抽象

分布函数

分布函数：
X为随机变量，$F(x)$定义为：
$$F(x)=P(X\le x)$$
定义域：$(-\infty ,\infty )$
值域： $[0,1]$

当$a<b$, $P(a<x\le b)=F(b)-F(a)$
性质：

1. 值域[0,1]
2. 若$a<b$，则$F(a)\le F(b)$
3. 右连续 $$\underset{x\to a^{+}}{\lim }F(x)=F(a)$$

$$\begin{gathered} \underset{x\to \infty }{\lim }F(x)=1 \\ \underset{x\to -\infty }{\lim }F(x)=0 \end{gathered}$$

离散型随机变量

定义

随机变量取值为离散的（有限或者可列）

三种常用分布

1. 0-1分布

2. 二项分布

3. 泊松分布

连续性随机变量

定义

随机变量X的分布函数可以表示为：
$$F(x)={\int }_{-\infty }^{x}f(u)du$$
F(x)为连续函数

$f(x)$为$X$的概率密度函数，其具有如下性质：

1. $$f(x)\ge 0$$
2. $${\int }_{-\infty }^{\infty }f(x)dx=1$$
3. $$P(x_1<X\le x_2)=F(x_2-x_1)$$
4. 若$f(x)$在$x$点连续，$F^{{}^{\prime }}(x)=f(x)$

注： $P(X=a)=0$

几种常用分布

1. 均匀分布
2. 指数分布
3. 正态分布

随机向量与分布

联合分布

二维离散随机变量

二维连续随机变量

边缘分布

1. 连续型
   

2. 离散型
   求和即可

条件分布

1. 离散型
2. 连续型
   

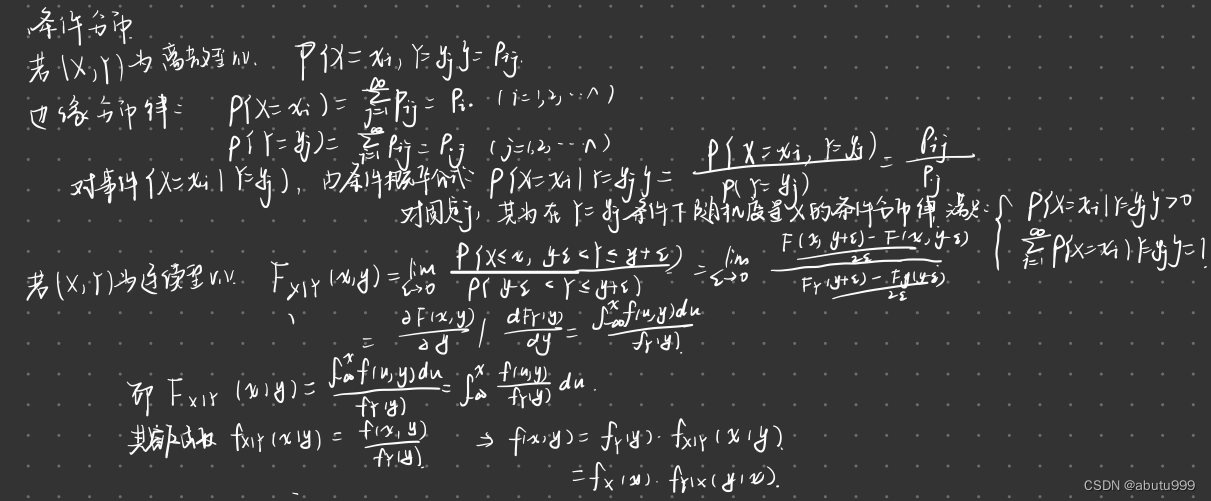
随机向量的独立性

$F(x,y)=F_X(x)F_Y(y)$

1. 离散(X,Y） 要求$p_{ij}=p_{i.}{p}_{.j}$
2. 连续(X,Y) 要求$f(x,y)=f_X(x)f_Y(y)$

随机向量函数分布

随机变量的函数的分布

1. 连续
   X为连续随机变量，分布函数为f(x)，y=g(x)为可导单调函数，则Y=g(X)为连续变量函数
   $$f_Y(y)=\{\begin{array}{ll}f[h(y)]|h^{{}^{\prime }}(y)|& \text{如果 }y在g(x)的值域内\\ 0& 其他\end{array}$$

h(y)为y = g(x)的反函数
2. 离散

两个随机变量函数的分布

$Z=g(X,Y)$,Z为分布函数

1. （X,Y)连续
   

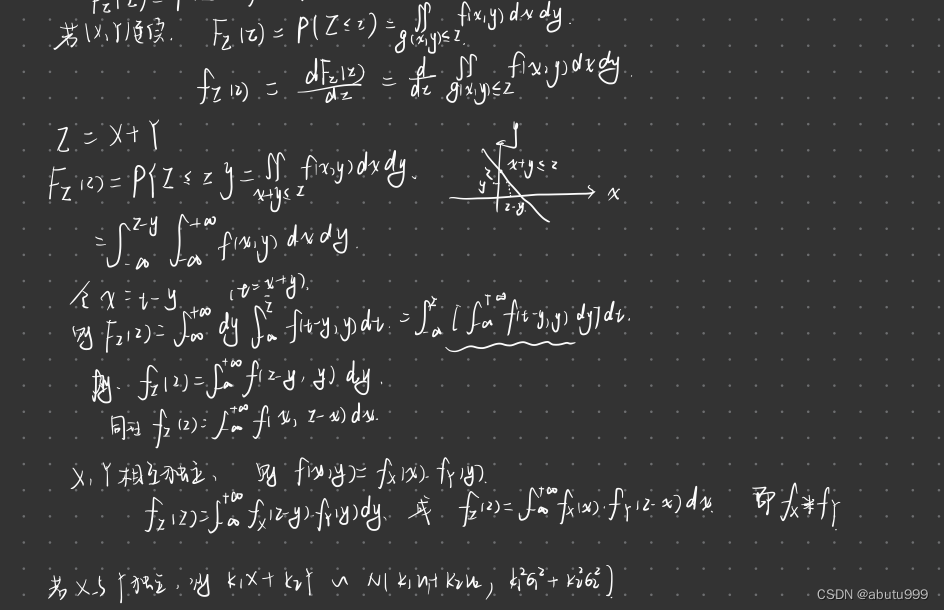
2. （X,Y)离散