题目描述:
给定 V 种货币(单位:元),每种货币使用的次数不限。
不同种类的货币,面值可能是相同的。
现在,要你用这 V 种货币凑出 N 元钱,请问共有多少种不同的凑法。
输入格式:
第一行包含两个整数 V 和 N。
接下来的若干行,将一共输入 V 个整数,每个整数表示一种货币的面值。
输出格式:
输出一个整数,表示所求总方案数。
数据范围:
1≤V≤25
1≤N≤10000
答案保证在long long范围内。
输入样例:
3 10
1 2 5
输出样例:
10分析步骤:
第一:我们可以看到题目要求我们统计出有多少种凑法,每种货币可以用无限次,只要不超过N元钱就可以,这就非常符合我们的完全背包问题,所以我们只需要运用背包DP的方法,就可以解出这道题目。
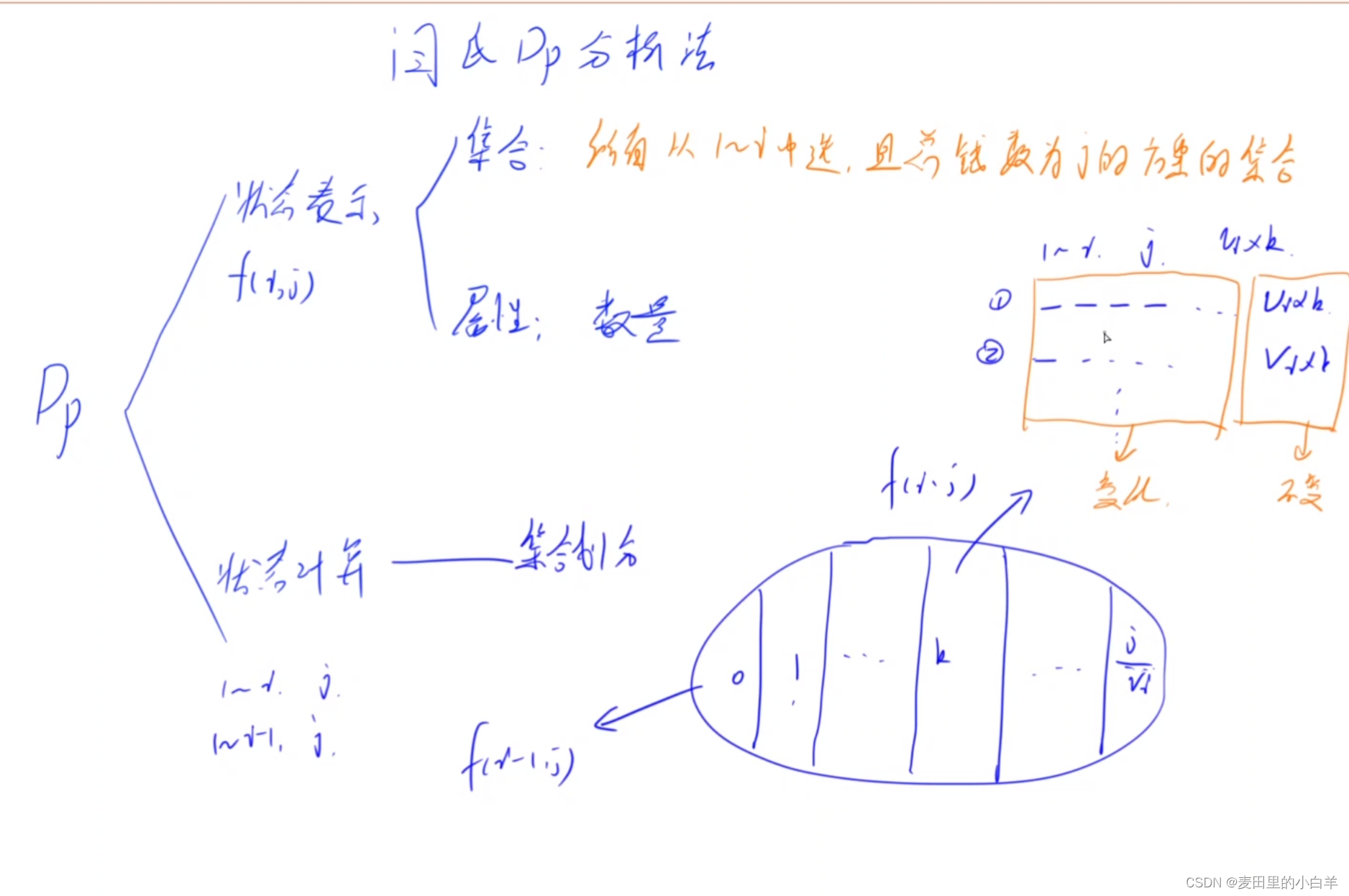
第二:运用闫氏DP分析法
-
根据闫氏DP分析法我们可以知道dp问题可以将其分解为两个步骤:第一种是状态表示,第二种是状态计算。
-
我们所有的背包问题都是围绕我们对于集合的定义来的,所以这个定义是非常重要的!!!我们将集合定义为:所有只从前i个货币中选择,总金额不超过 j 的方案的集合。
-
状态计算:由于完全背包是可以无限次的选择物品的,所以我们不能和01背包一样,只将其分解为选或者不选,因为它可以有很多很多种选择,可以不选,可以选一种,可以选两种...只要金额(背包体积)足够大就可以。
-
如果他不选择物品 i 那么这种情况相当于从(1,i - 1)中选择金额不超过j的情况是一样的所以我们的表达式是:f[i-1][j]。
-
如果他选择物品 i 那么这样又该如何表示呢?我们并不知道他到底要选择几个物品,那应该怎么做呢?假如我们选择一个的话那么就应该写为f[i-1][j-vi];假如我们选择两个的话那么就应该写为f[i-1][j-2*vi];假如我们选择k个的话那么就应该写为f[i-1][j-k*vi],那么我们最终的答案就应该在这些集合之中。
-
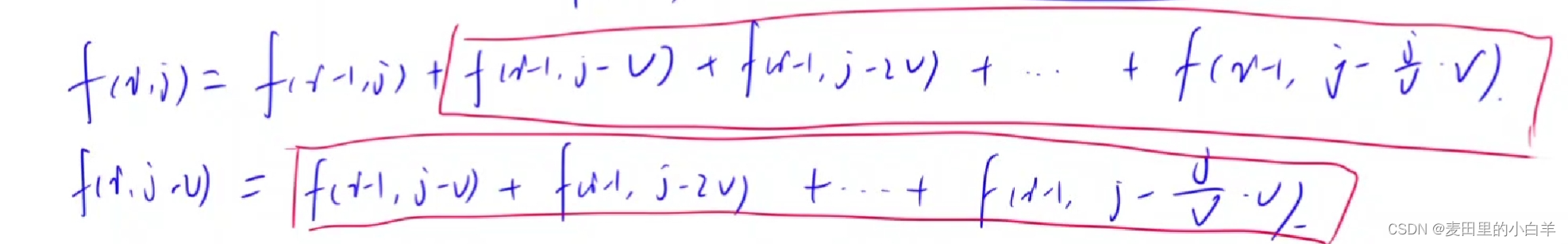
-
所以f(i,j) = f(i-1 , j) + f(i-1 , j - v) + f(i-1 , j - 2v) + ........+f(i-1 , j - (j/v)*v);
-
所以f(i,j-v) = f(i-1 , j - v) + f(i-1 , j - 2*v) + f(i-1 , 3*v) + ........f(i-1 , j - (j/v)*v);
-
由上述两个式子,我们可以知道如果将 j 替换成 j-vi 两个式子非常相似。f[ i ] [ j ] = f[ i -1][ j ] + f[ i ][ j - vi ] ;
第三:书写主函数,构建整体架构:
-
输入值,更新我们的初始状态f[0][0] = 1。为什么等于1?因为围绕我们的定义:只从前i个货币中选择,总金额不超过 j 的方案的集合。所以f[0][0]表示的是在前0个货币中选总金额为0时的方案数为1,因为都不选也是一种方案。
-
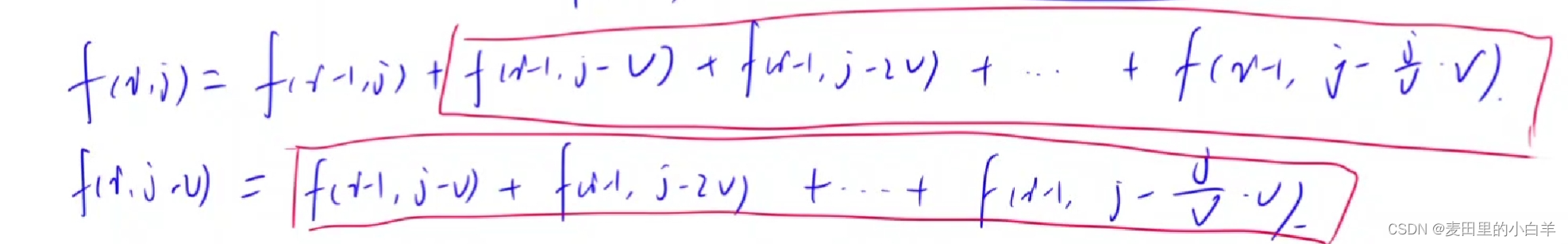
-
for循环输入货币的面额,for循环去遍历金额的大小从0开始,根据上图的公式我们可以推断出来f[i][j] = f[i-1][j] + f[i][j-x];所以利用此公式我们就可以得出答案。但是注意一个问题:选择一个,选择两个,是在金额大于我们的货币面值的情况下才可以选,假如答案的金额都要小于货币面额的话就不可以选了!
-
。所以加一个判断只有j(金额) >= x(货币面额)才可以去选择。
for(int j = 0 ; j <= m ; j ++){
f[i][j] = f[i-1][j];
if(j >= x) f[i][j] += f[i][j-x];
}01背包从后往前,完全背包从前往后!!
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 30 , M =10010;
typedef long long LL;
LL n , m;
LL f[N][M];
int main()
{
cin>>n>>m;
f[0][0] = 1;
for(int i = 1 ; i <= n ; i ++ ){
int x ;
cin>>x;
for(int j = 0 ; j <= m ; j ++){
f[i][j] = f[i-1][j];
if(j >= x) f[i][j] += f[i][j-x];
}
}
cout<<f[n][m];
return 0;
}