Matplotlib数据可视化实战-2绘制折线图（2）

news2024/9/28 11:20:04

2.11营业额可视化

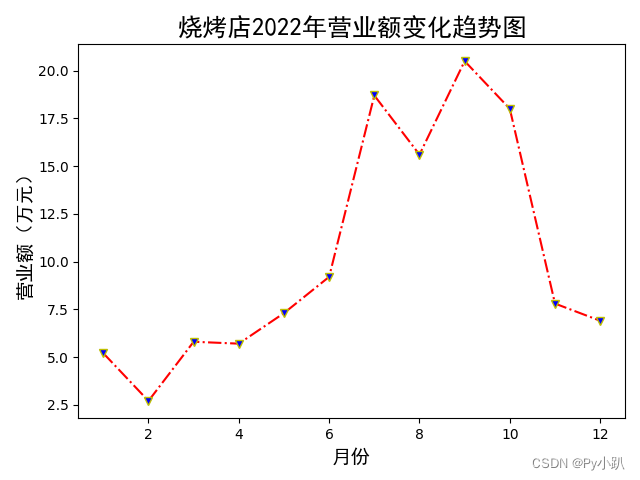
已知某学校附近一个烧烤店2022年每个月的营业额如下图所示。编写程序绘制折线图对该烧烤店全年营业额进行可视化，使用红色点画线连接每个月的数据，并在每个月的数据处使用三角形进行标记。

烧烤店营业额
月份	1	2	3	4	5	6	7	8	9	10	11	12
营业额/万元	5.2	2.7	5.8	5.7	7.3	9.2	18.7	15.6	20.5	18.0	1.8	6.9

运行结果如下：

import matplotlib.pyplot as plt

# 月份和每月营业额
month = range(1, 13)
money = [5.2, 2.7, 5.8, 5.7, 7.3, 9.2, 18.7, 15.6, 20.5, 18.0, 7.8, 6.9]

plt.plot(month, money, 'r-.v', mfc='b', mec='y')
plt.xlabel('月份', fontproperties='simhei', fontsize=14)
plt.ylabel('营业额（万元）', fontproperties='simhei', fontsize=14)
plt.title('烧烤店2022年营业额变化趋势图', fontproperties='simhei', fontsize=18)
# 紧缩四周空白，扩大绘图区域可用面积
plt.tight_layout()

plt.show()

参数mfc（marker face color）用来设置散点符号内部颜色

参数mec（marker edge color）设置散点符号边线颜色

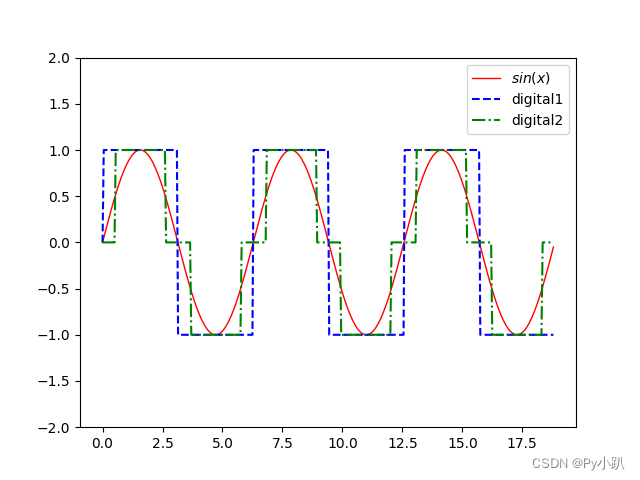
2.12绘制折线图模拟连续信号与数字信号

import numpy as np
import matplotlib.pyplot as plt

t = np.arange(0, 6*np.pi, 0.05)
# 连续信号与数字信号的函数值
t_sin = np.sin(t)
t_digital1 = np.piecewise(t_sin, [t_sin>0, t_sin<0], [1,-1])
t_digital2 = np.round_(t_sin)

plt.plot(t, t_sin, label='$sin(x)$', color='red', lw=1)
plt.plot(t, t_digital1, 'b--', label='digital1')
plt.plot(t, t_digital2, 'g-.', label='digital2')
plt.ylim(-2.0, 2.0)
plt.legend()

plt.show()

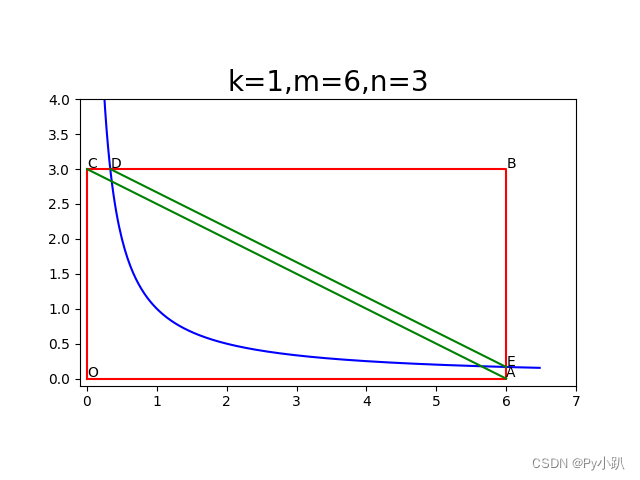
2.13在第一象限中，任意反比例函数xy=k与任意矩形OABC的两个交点的连线始终与矩形的对角线平行，请编写程序验证这一点。

import numpy as np
import matplotlib.pyplot as plt

k = 1                                          # 反比例函数xy=k的常数k
m, n = 6, 3                                    # 矩形右上角坐标(m,n)
x = np.arange(0.1, m+0.5, 0.02)                # 第一象限中反比例函数曲线上顶点的x坐标
y = k / x                                      # 根据反比例函数xy=k计算顶点y坐标
plt.plot(x, y, 'b')                            # 绘制第一象限指定区间内的反比例函数图像

plt.plot([0,m,m,0,0], [0,0,n,n,0], 'r')        # 绘制矩形，从左下角出发，向右、上、左、下
plt.plot([0,m], [n,0], 'g')                    # 矩形对角线
plt.plot([k/n,m], [n,k/m], 'g')                # 矩形与反比例函数的交点连线

for x, y, ch in zip([0,m,m,0,k/n,m], [0,0,n,n,n,k/m], 'OABCDE'):
    plt.text(x, y+0.02, ch)                    # 绘制顶点与交点的符号
plt.xlim(-0.1, m+1)                            # 设置坐标轴跨度
plt.ylim(-0.1, n+1)
plt.title(f'k={k},m={m},{n=}', fontsize=20)   # 设置图形标题
plt.gca().set_aspect(True)                     # 设置图形纵横比相等

plt.show()                                     # 显示图形

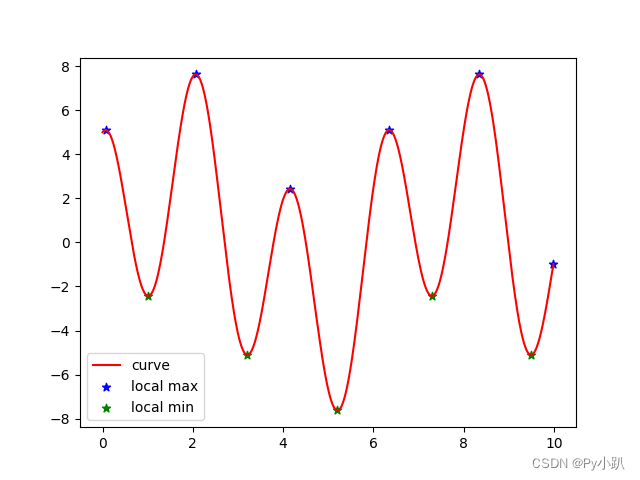
2.14绘制函数曲线，计算并标记极值

import numpy as np
import matplotlib.pyplot as plt

# 函数自变量取值范围区间
start, end = 0, 10
# 计算所有采样点的x坐标、y坐标，绘制折线图
x = np.arange(start, end, 0.01)
y = 3*np.sin(x) + 5*np.cos(3*x)
s, = plt.plot(x, y, 'r-')
# 设置子区间长度，在每个子区间（不包含端点）内寻找极值
# 调整区间大小时会影响极值数量，应使得每个子区间内都包含波峰和波谷
span = 66

for start in range(0, len(y), span):
    # 每个子区间的自变量与函数值
    sectionY = y[start:start+span]
    sectionX = x[start:start+span]
    # 局部最大值和局部最小值
    localMax = sectionY.max()
    localMin = sectionY.min()

    # 方案一：
    # 按值大小升序排序的索引
    argsort_result = sectionY.argsort()
    # 区间内所有最大值的索引和所有最小值的索引
    args_max = argsort_result[-len(sectionY[sectionY==localMax]):]
    args_min = argsort_result[:len(sectionY[sectionY==localMin])]
    # 去除子区间端点
    args_max = list(set(args_max)-{0,span-1})
    if args_max:
        s1 = plt.scatter(sectionX[args_max], sectionY[args_max], marker='*', c='b')
    
    args_min = list(set(args_min)-{0,span-1})
    if args_min:
        s2 = plt.scatter(sectionX[args_min], sectionY[args_min], marker='*', c='g')

    # 方案二：
##    for index, yy in enumerate(sectionY):
##        if yy==localMax and index not in (0, span-1):
##            # 在极大值处绘制一个蓝色五角星
##            s1 = plt.scatter(sectionX[index], yy, marker='*', c='b')
##        elif yy==localMin and index not in (0, span-1):
##            # 在极小值处绘制一个绿色五角星
##            s2 = plt.scatter(sectionX[index], yy, marker='*', c='g')

# 创建图例
plt.legend([s,s1,s2], ['curve','local max','local min'])
#显示绘制的结果
plt.show()

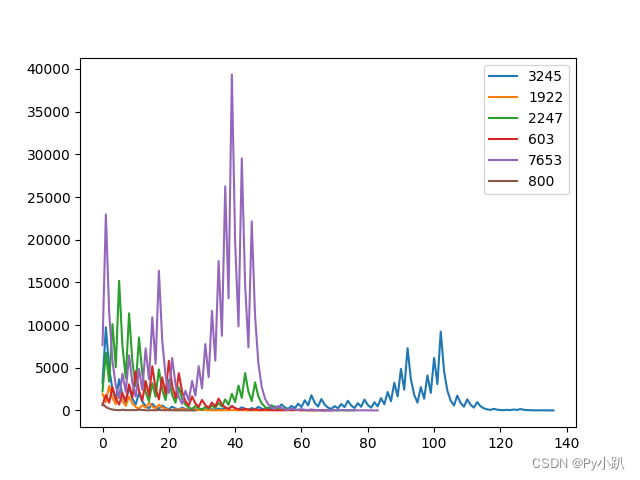
2.15使用折线图可视化角谷猜想

角谷猜想，也被称为“冰雹猜想”或“3n+1猜想”，是一个数学上的未解问题。这个猜想的内容是，对于任意一个正整数，如果是奇数，则乘3再加1，如果是偶数，则除以2，这样得到的结果再按照上述规则重复处理，最终总能够得到1。

角谷猜想的名称来源于其在不同地方的流传历史。它首先在美国流传开来，然后传播到欧洲。后来，一位名叫角谷的日本人将其带到亚洲，因此得名“角谷猜想”。而“冰雹猜想”的名称则来源于这个猜想处理数字时数字上上下下的变化过程，就像冰雹在高空中形成并落下的过程一样。

尽管角谷猜想自提出以来已经经过了许多数学家的研究，但至今仍然没有找到证明或反证。这个猜想在数学界引起了广泛的关注，甚至有一些数学家悬赏求解。

from random import choice, seed
import matplotlib.pyplot as plt

def check(num):
    times = 0         # 变为1所需要的次数
    numbers = [num]   # 变为1的过程中的所有数字
    while True:
        times = times + 1
        if num%2 == 0:
            num = num // 2
        else:
            num = num*3 + 1
        numbers.append(num)
        if num == 1:
            # 变为1时结束循环
            break
    return range(times+1), numbers

seed(20220702)
for _ in range(6):
    num = choice(range(1, 9999))
    plt.plot(*check(num), label=str(num))
    
plt.legend()
plt.show()

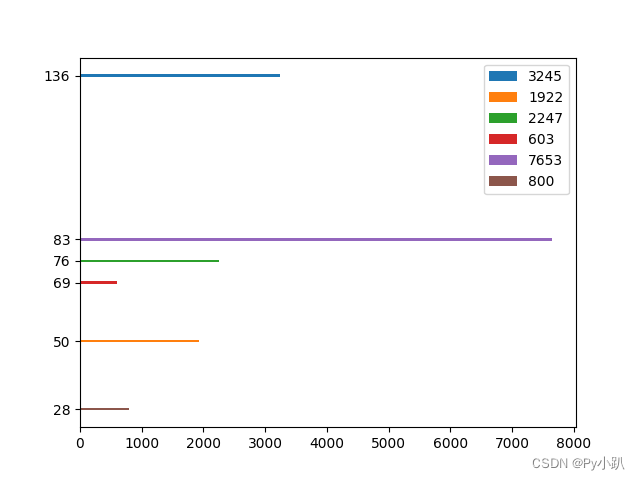
2.16角谷猜想中正整数最终变为1所需要的计算次数

from random import randrange, seed
import matplotlib.pyplot as plt

def check(num):
    times = 0
    while True:
        times = times + 1
        if num%2 == 0:
            num = num // 2
        else:
            num = num*3 + 1
        if num == 1:
            break
    return times

ticks = []
seed(20220702)
for _ in range(6):
    num = randrange(1, 9999)
    tick = check(num)
    ticks.append(tick)
    # 第一个参数表示y坐标，表示每个柱的位置，对应变为1所需要的次数
    # 第二个参数表示长度，对应要变为1的数字
    plt.barh(tick, num, label=str(num))
# 在每个柱对应的位置显示刻度
plt.yticks(ticks)
plt.legend()

plt.show()