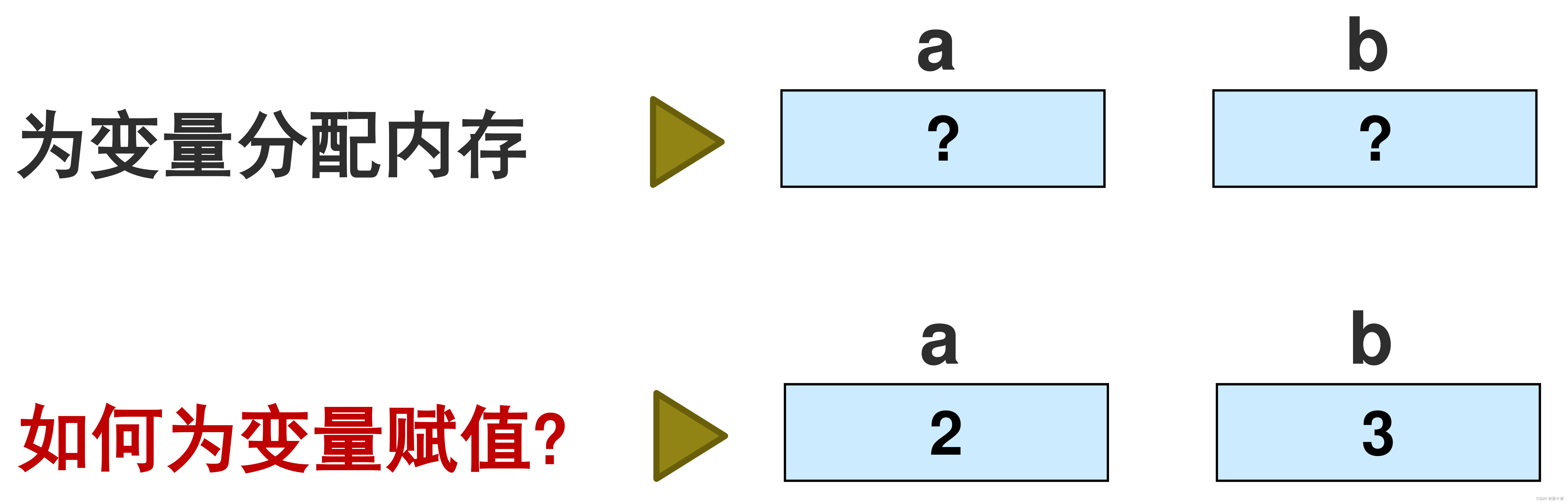
1.什么是代数(algebra)?
为了形式化一个概念,构建出有关这个概念的符号以及操作符号的公式。
2.什么是线性代数(linear algebra)?
一项关于向量以及操作向量的公式的研究。
3.举一些向量的例子?
- 几何向量(Gemometric vectors):可以进行add操作也可以multiply by标量,帮助我们在方向direction和大小magnitude方面去推理数学操作。
- 多项式(Polynomial):y=x2+x3+x4...
- 音频信号(Audio signals):音频信号是一系列数字,我们可以把音频信号加和(add),亦可以以一定λ大小扩大(multiply)。
:n元组是指n维向量,也是为了方便编程语言中array的表示。
4.什么是线性方程组(system of linear equation)?
其中,是这个式子的未知量,每一个满足这个方程组的n元组都可以称为线性方程组的一个解。
5.实数线性方程组的解(solution)有哪些情况?
要么无解,要么有一个解,要么有多个解。
如果是,那么可以看做二维平面两条直线相交,那么结果是1.无交集2.一个点3.一条直线。如果是
,那么可以看做是在三维立体空间两个平面相交,结果可能是1.一个平面2.一条直线3.一个点4.空。
6.什么是点积(dot product),也称作Hadamard product?
对于元素,我们用矩阵A的第i行与矩阵B的第j列逐个元素相乘,然后相加。
7.什么是单位矩阵(Identity Matrix)?
在n阶方阵中,只是在对角(diagonal)元素值为1,在其他元素值为0。
8.矩阵有哪些性质(property)?
- 结合性:

- 分配性:
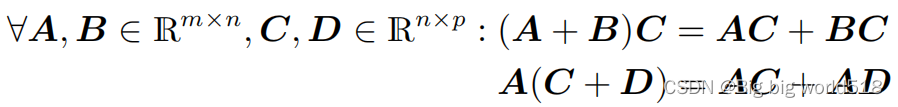
- 和单位矩阵相乘:

9.什么是矩阵的逆(inverse)?
对于n行n列的矩阵A和n行n列的矩阵B,如果满足,B被叫做A的逆。如果B存在,那么称A为正则矩阵/可逆矩阵/非奇异矩阵(regular/invertible/nonsingular)。如果矩阵的行列式(determinant)不为零,那么可以认为矩阵可逆。
10.什么是矩阵的转置(transpose)?
对于m行n列的矩阵A,A的转置B是n行m列,A的每一行作为B的每一列。如果A可逆,那么B(A的转置)爷可逆。
11.关于矩阵的逆和矩阵的转置的性质?
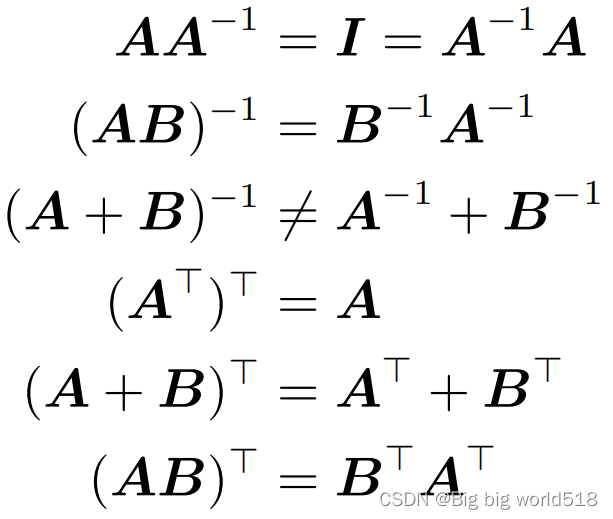
12.求解线性方程组的过程?
- 寻找
的特解
- 寻找
的所有解
- 将步骤一和步骤二的所有解结合起来得到通解(general solution)
13.什么是高斯消元法(Gaussian elimination)
高斯消元法是通过初等变换(elementary transformation)把一个线性方程组的增广矩阵(augmented matrix),譬如,那么其增广矩阵为
,变成一个行递减的形式(reduced row-echelon)。
14.行递减阶梯矩阵有什么特点?
- 是一个行阶梯的形式
- 每个枢轴的值都是1
- 每一列只有唯一一个枢轴是这一列不为零的值
15.什么是广义逆矩阵(Moore-Penrose pseudo-inverse)?
通常情况我们定义逆矩阵针对的是方阵,但是如果一个非方阵矩阵,它的各个列向量是线性无关(linear independent),那么我们我们可以使用如下方法求解:
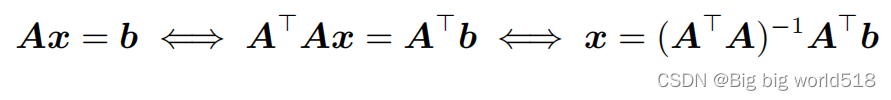
其中解被称为广义逆矩阵。