基础数据结构(蓝桥杯Python组)

链表

基础概念

链表可以快速插入、删除元素，用于存储数据。

每个节点维护两个部分:数据域和指针域
数据域就是节点所存储的数据，指针其实就是下标（next，节点的下一个节点在哪）
链表维护head和tail，每次从tail处插入新元素

但是在python中列表就够大部分应付大部分情况了

蓝桥1111

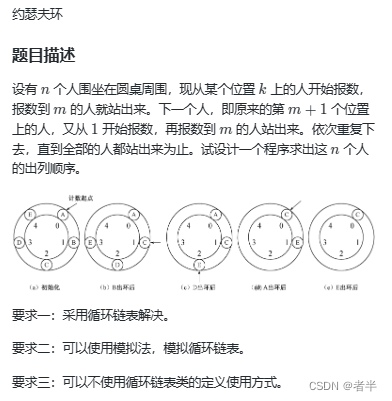
首先想的暴力做法，环可以看作多个列表相乘，这样可以一次遍历到底（直到满足条件）

n, k, m = map(int, input().split())
a = list(range(1, n + 1)) * 200
vis = []
count = 0
for i in range(k - 1, len(a)):
  if a[i] in vis:
    continue
  count += 1
  if count == m:
    vis.append(a[i])
    count = 0
  if len(vis) == n:
    break
for i in vis:
  print(i)

模拟链表做法：

n, k, m = map(int, input().split())
a = list(range(1, n + 1))
i = k - 1
while len(a) != 0:
  i = (i + (m - 1)) % len(a)
  print(a.pop(i))

栈

基础概念

先进后出的数据结构
每次添加的元素放入栈顶，每次取出的元素也是栈顶

可以理解位电梯，后进的人先出，先出的人后出。（因为电梯口可以先出去）

可以直接用list模拟
添加元素:a.append(x)
获取栈顶元素:a[-1]
去除栈顶元素:a.pop()

栈的应用：

十分广泛，比如括号匹配问题，表达式求值，递归机制。

利用先进后出策略解决问题

蓝桥2490

一开始的想法：

import os
import sys

# 请在此输入您的代码
n = int(input())
a = list(input())
stack = []
for i in a:
  if i == '(':
    stack.append(i)
  else:
    if len(stack) == 0:
      stack.append(1)
      break
    stack.pop()
if len(stack) != 0:
  print('No')
else:
  print('Yes')

后来参考的做法：

import os
import sys

# 请在此输入您的代码
n = int(input())
a = list(input())
stack = []
ok = True
for i in a:
  if i == '(':
    stack.append(i)
  else:
    if len(stack) == 0:
      ok = False
      break
    stack.pop()
if ok and len(stack) == 0:
  print('Yes')
else:
  print('No')

蓝桥3194

import os
import sys

# 请在此输入您的代码
s = input()
s = s.replace('5', '')
s = s.replace('7', '')
s = s.replace('6', '9')
s = list(s)
a = []
for i, c in enumerate(s):
  if c == '3':
    a.append(i)
  elif c == '4' and len(a) != 0:
    idx = a.pop() # 前一个3的下标：idx
    s[i], s[idx] = s[idx], s[i]
print(''.join(s))

队列

基础概念

先进先出的数据结构

每次添加的元素放入队尾，每次取出的元素是队首

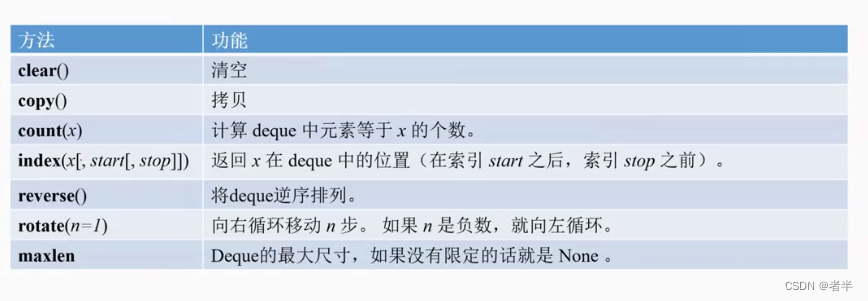
可以用List模拟，但是deque效率更高

蓝桥511

import os
import sys
from collections import deque
# 请在此输入您的代码
M, N = map(int, input().split())
a = list(map(int, input().split()))
q = deque()
ans = 0
for x in a:
  if x in q:
    continue
  else:
    ans += 1
    q.append(x)
    if len(q) > M:
      q.popleft()
print(ans)

堆

基础概念

堆:完全二叉树，每个节点小于等于子节点(默认为最小堆)

每个节点k都有两个子节点2k+1，2k+2

堆的功能就是维护一个最小值/最大值

可以加一个元素，获取当前的最小值，删一个最小值。

import heapq
a = [11, 6, 9, 8, 7, 3]
heapq.heapify(a)
print("a = ", a)
heapq.heappush(a, 4)
print("a = ", a)
while len(a):
    print(heapq.heappop(a), end=" ")

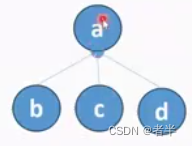
把原有的列表变为如下图的形式，每个父节点都小于子节点

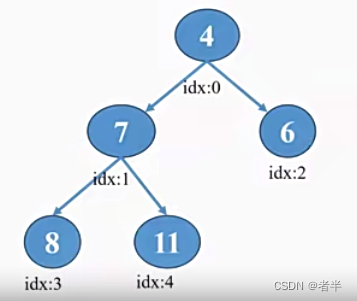
添加元素4：

先添加到末尾
然后不断往上提

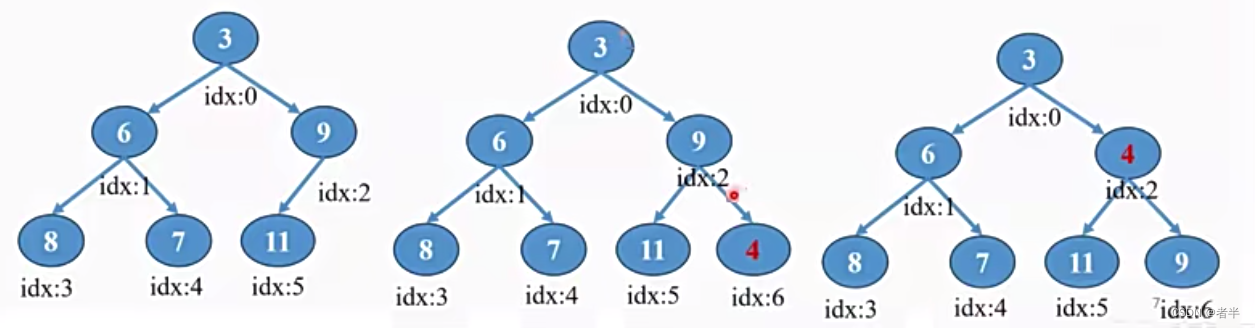
删除最小元素：

先获取a[0],然后将最末尾值放入a[0]
然后不断往下放（左右儿子选择小的那个进行交换）

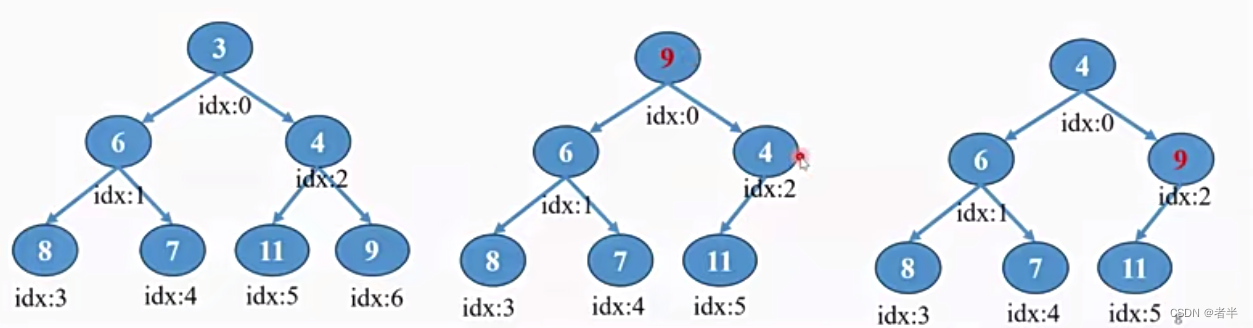
优先队列

先进，按照优先级出。
非严格来说，优先队列就是堆。
优先队列是一种抽象数据类型，可以使用不同的数据结构来实现，其中基于堆的实现方式比较常见。

一般我们使用优先队列采用queue库中的PriorityQueue

# 定义优先队列
from queue import PriorityQueue
pq = PriorityQueue()
# 元素x入队
pq.put(3)
pq.put(2)
pq.put(1)
# 获取最小元素
print(pq.queue[0])
# 取出最小元素
print(pq.get()) # 取出来并删掉
print(pq.get())
print(pq.get())

底层实现仍然是先前的heapq

# 定义优先队列
from queue import PriorityQueue
pq = PriorityQueue()
# 元素x入队
pq.put(3, "Banana")
pq.put(1, "Apple")
pq.put(1, "Car")
# 获取最小元素
print(pq.queue[0])
# 取出最小元素
print(pq.get())
print(pq.get())
print(pq.get())

比较第一个谁小谁先出，如果第一个一样小，那么比较第二个。

日常使用的时候要保证put的结构相同。

蓝桥3749

import os
import sys

# 请在此输入您的代码
from queue import Queue, PriorityQueue
N, X = map(int, input().split())
a = list(map(int, input().split()))
q = Queue() # 维护当前打印队列
pq = PriorityQueue() # 维护最小优先级（默认小根堆），加个负号就行

for i, x in enumerate(a):
  q.put((i, x)) # 下标i和x，为了判断是否是小蓝的任务，以及重要程度。
  pq.put(-x) # 维护最大值

ans = 0
while True:
  i, x = q.get()
  if -x == pq.queue[0]:
    pq.get()
    ans += 1
    if i == X:
      print(ans)
      break
  else:
    q.put((i, x))

ST表

RMQ问题

Range Maximum/Minimum Query，称为RMQ问题，求区间最大/最小值
模板题:给定n个数字，有m次询问，每次询问需要回答区间[L,r]中的最大值/最小值。
求解思路:暴力做法，对于每次询问，都暴力求解即可
时间复杂度O(mn)

如何优化呢？ ST表启动

基础概念：

ST表可用于解决可重复贡献问题:对于运算opt满足xoptx=x，且运算满足结合律，对应的区间询问就是可重复贡献问题。

例如:区间最值(max(x,x)=x)、区间按位和(x&x=x)、区间按位或(x|x=x)、区间gcd(gcd(x,x)=x)

ST表利用倍增思想和动态规划来预处理答案:

f(i,j)表示区间 $eq?%5Bi%2Ci+2%20%5E%7Bj-1%7D%20%5D$ 的最大值
区间长度为 $eq?2%5E%7Bj%20-%201%7D$

$eq?f%28i%2C0%29%3D%20a%5Ei$

$eq?f%28i%2Cj%29%20%3D%20max%28f%28i%2Cj-1%29%2Cf%28i+%202%5E%7Bj-1%7D%2Cj-1%29%29$

$eq?%5Bi%2C%20i%20+%202%5E%7Bj%7D%20-%201%5D$ ， $eq?%5Bi%2C%20i%20+%202%5E%7Bj%20-%201%7D%20-%201%5D$ ， $eq?%5Bi%20+%202%5E%7Bj%20-%201%7D%2C%20i+%202%5E%7Bj%20-%201%7D%20+%202%5E%7Bj%20-%201%7D%20-%201%5D$

相当于把大区间一分为二，成了两个小区间。

而大区间的最大值等于两个子区间的最大值。

这边要以j作为第一重循环，因为用i来更新，后面的值没办法更新。

对于询问[l,r]，求 $eq?s%3Dlog_%7B2%7D%5E%7B%7D%28r-l+1%29$ ，则转换成区间: $eq?%5Bl%2Cl+%202%5Es-1%5D%5Cbigcup%20%5Br-2%5Es%20+%201%2Cr%5D$

$eq?f%28l%2Cr%29%3D%20max%28f%28l%2Cs%29%2Cf%28r-2%5Es+1%2Cs%29%29$

蓝桥1205

import os
import sys
import math

# 请在此输入您的代码
# 求最大值st表
def st_init(n, a):
  L = math.ceil(math.log2(n)) + 1 # 向上取整
  # f[i][j]表示区间[i, i + 2 ^ j - 1]的最大值
  f = [[0] * L for i in range(n)]
  # 边界
  for i in range(n):
    f[i][0] = a[i]
  # 打表
  for j in range(1, L):
    pj = 1 << (j - 1)
    for i in range(n - pj):
      f[i][j] = max(f[i][j - 1], f[i + pj][j - 1])
  return f

# 查询区间[l, r]
def query(f, l, r):
  s = int(math.log2(r - l + 1))
  return max(f[l][s], f[r - (1 << s) + 1][s])

N, Q = map(int, input().split())
a = list(map(int, input().split()))
f = st_init(N, a)
for _ in range(Q):
  l, r = map(int, input().split())
  l, r = l - 1, r - 1
  print(query(f, l, r))

树

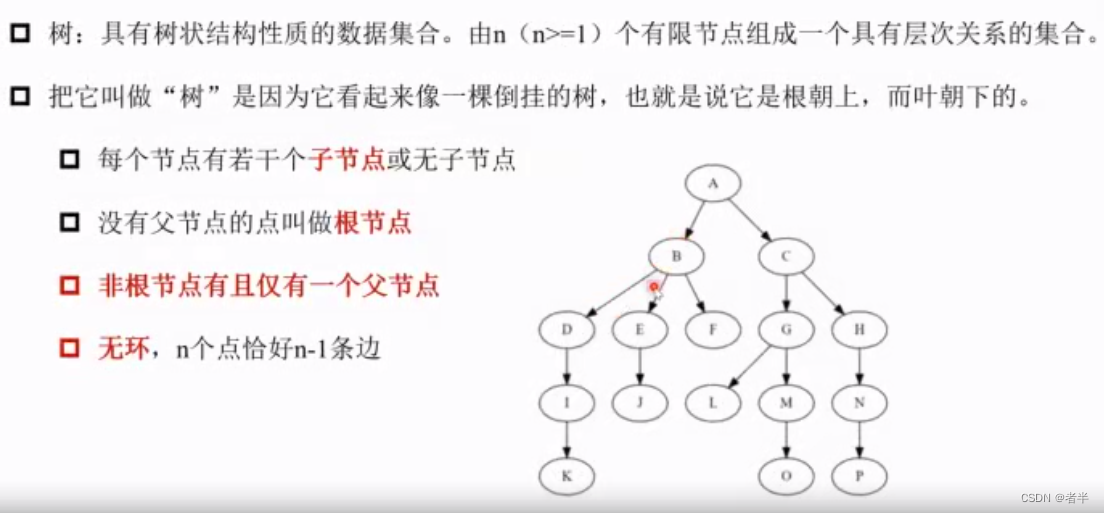
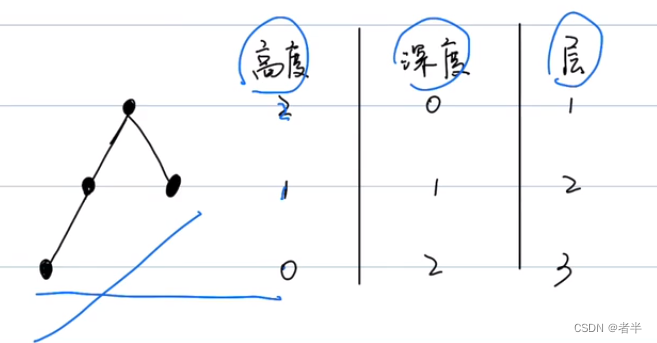
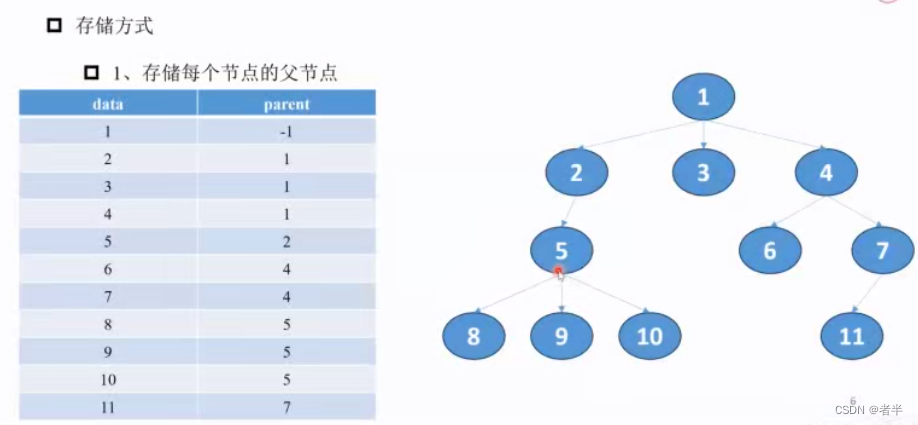
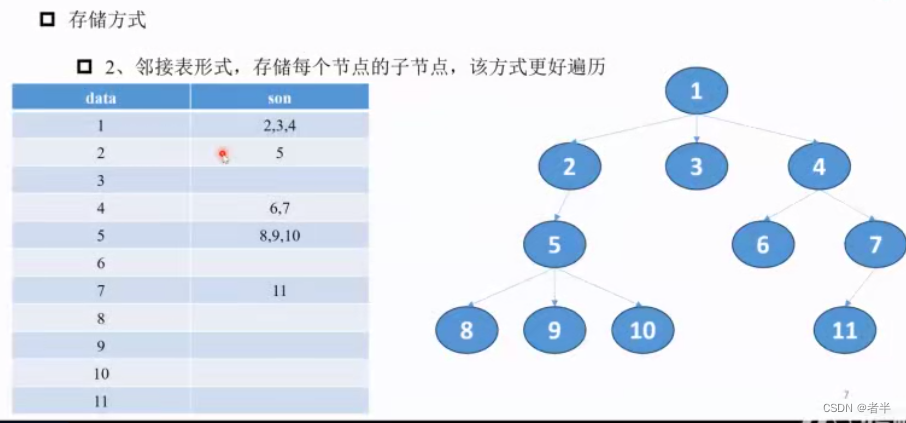
二叉树

二叉树概念

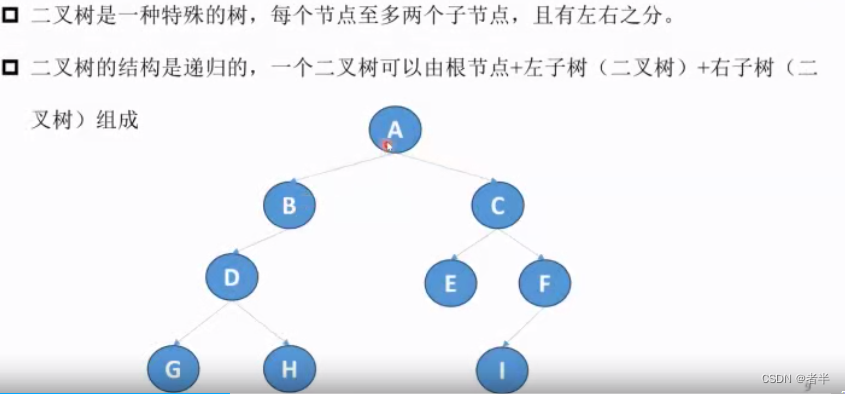
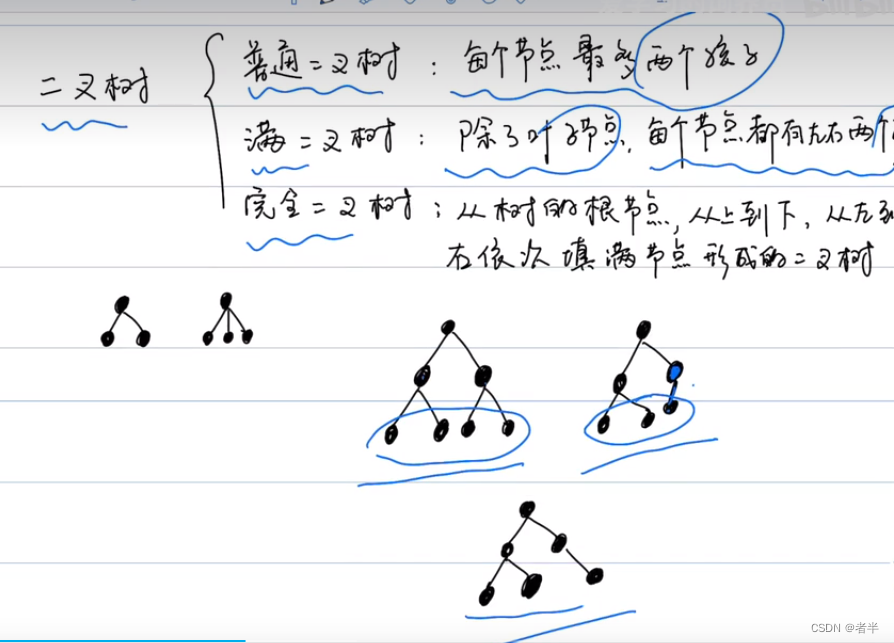
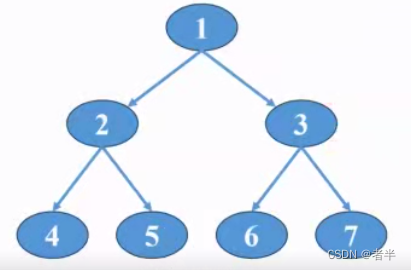
class TreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None
def CreateBinaryTree(nums):
        if not nums:
            return None
        def helper(index):
            if index >= len(nums) or nums[index] is None:
                return None
            node = TreeNode(nums[index])
            node.left = helper(2 * index)
            node.right = helper(2 * index + 1)
            return node
        root = helper(1)
        return root

二叉树的遍历：

代码的示例图：

先序

def preorderTraversal(root):
    if root is None:
        return []
    result = []

    def traverse(node):
        if node is None:
            return
        result.append(node.val)
        traverse(node.left)
        traverse(node.right)
        
    traverse(root)
    return result

x = [None] + ['A', 'B', 'C', 'D', None, 'E', 'F', 'G', 'H', None, None, None, None, 'I']
root = CreateBinaryTree(x)
print(preorderTraversal(root))

中序和后序

# 中序
traverse(node.left)
result.append(node.val)
traverse(node.right)

# 后序
traverse(node.left)
traverse(node.right)
result.append(node.val)

层序

from collections import deque
def levelOrderTraversal(root):
    if root is None:
        return []
    result = []
    queue = deque()
    queue.append(root)
    while queue:
        node = queue.popleft()
        result.append(node.val)
        if node.left is not None:
            queue.append(node.left)
        if node.right is not None:
            queue.append(node.right)
    return result
root = CreateBinaryTree(x)
print(levelOrderTraversal(root))

想要同时知道深度？

from collections import deque
def levelOrderTraversal(root):
    if root is None:
        return []
    result = []
    queue = deque()
    queue.append((root, 1))
    while queue:
        node, deep = queue.popleft()
        result.append((node.val, deep))
        if node.left is not None:
            queue.append((node.left, deep + 1))
        if node.right is not None:
            queue.append((node.right, deep + 1))
    return result
root = CreateBinaryTree(x)
print(levelOrderTraversal(root))

输入：

x = [None] + ['A', 'B', 'C', 'D', None, 'E', 'F', 'G', 'H', None, None, None, None, 'I']

输出结果：

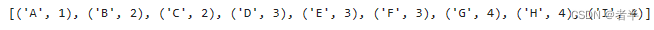
dfs和bfs代码示例图：

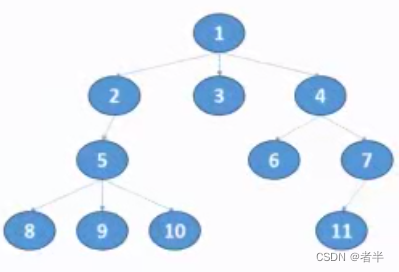
dfs单向边

def dfs(u): # 单向边
    print(u)
    for v in Tree[u]:
        dfs(v)
n = 11
Tree = [[] for i in range(n + 1)]
Tree[1] = [2, 3, 4]
Tree[2] = [5]
Tree[4] = [6, 7]
Tree[5] = [8, 9, 10]
Tree[7] = [11]
root = 1
dfs(root)

dfs双向边

def dfs(u, fa):
    print(u)
    for v in Tree[u]:
        if v == fa: continue
        dfs(v, u)
n = 11
Tree = [[] for i in range(n + 1)]
Tree[1] = [2, 3, 4]
Tree[2] = [5]
Tree[4] = [6, 7]
Tree[5] = [8, 9, 10]
Tree[7] = [11]
root = 1
dfs(root, -1)

bfs

from collections import deque

def bfs(root):
    result = []
    queue = deque()
    queue.append(root)
    
    while queue:
        u = queue.popleft()
        result.append(u)
        for v in Tree[u]:
            queue.append(v)
    
    return result

n = 11
Tree = [[] for _ in range(n + 1)]
Tree[1] = [2, 3, 4]
Tree[2] = [5]
Tree[4] = [6, 7]
Tree[5] = [8, 9, 10]
Tree[7] = [11]
root = 1

print(bfs(root))

直径和重心

待更...

LCA

待更新...

树状数组

待更新...

蓝桥183

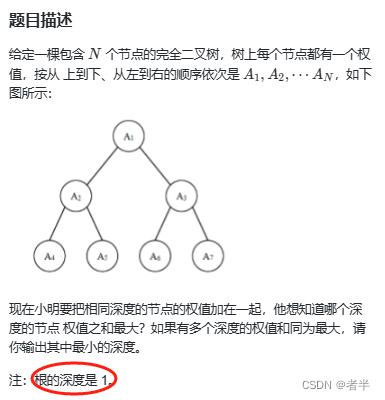
import os
import sys

# 请在此输入您的代码
import math
n = int(input())
a = [0] + list(map(int, input().split()))
h = int(math.log2(n)) + 1
tot = [0] * (h + 1)
for i in range(1, h + 1):
  tot[i] = sum(a[(1<<(i - 1)):(1<<i)])
print(tot.index(max(tot)))

并查集

N个互不相交的集合，需要进行以下两类操作

合并两个集合
判断两个集合是否属于同一集合

传统方法

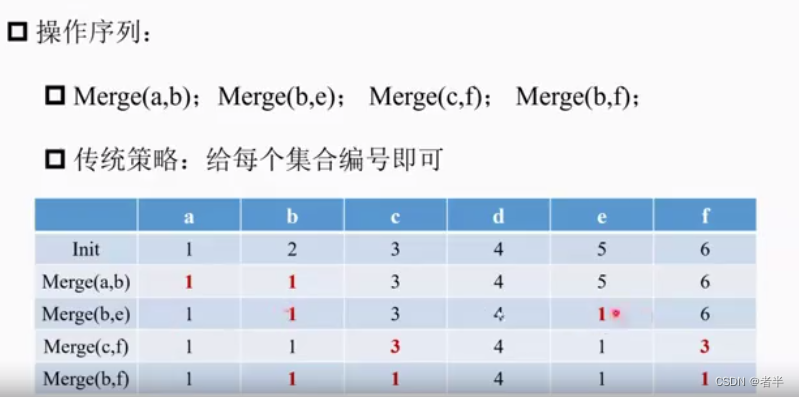
比如Merge(a,b)就是把ab合并，传统办法就是进行编码，将b的所有2改为1，说明是一个集合里的。

每个点都要改，操作O(n)

基础概念

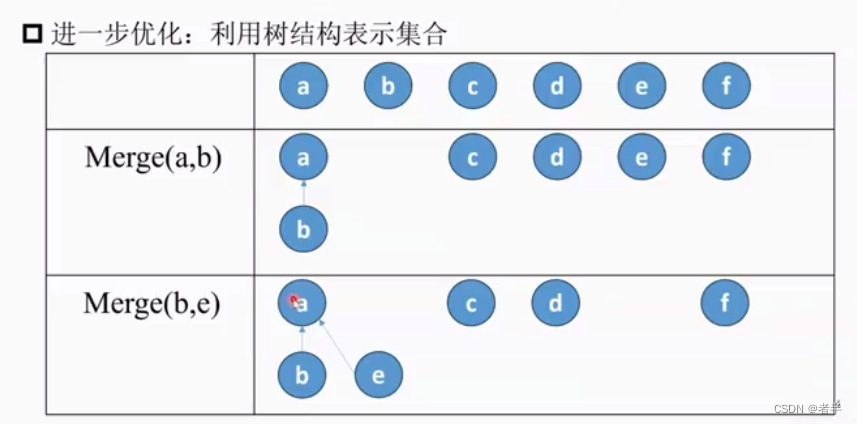
注意Merge(b, e)连接的是b的根节点

而Merge(b,f)是f的树连接到b的树

也就是根节点相连

模板

暴力找父节点：

def Findroot(x):
    # 不断找父节点，直至父节点等于自己。
    while x != p[x]: # 没有找到跟节点，不断往上走。
        x = p[x]
    return x
def Merge(x, y):
    rootx = Findroot(x)
    rooty = Findroot(y)
    p[rootx] = rooty
    
def Query(x, y):
    rootx = Findroot(x)
    rooty = Findroot(y)
    return rootx == rooty
# p[x]表示x的父节点编号
n = int(input())
p = list(range(n+1))

链式找父节点，此时时间消耗大，那就路径压缩。

路径压缩：每次寻找根节点时，将路径上所有点直接连接到根节点。

def Findroot(x):
    if x == p[x]: return x
    p[x] = Findroot(p[x]) # 直接将根节点作为父节点
    return p[x]

只要找过一遍，就变成右边的O(1)，一步就能找到根。

蓝桥1135

import os
import sys
input = sys.stdin.readline


# 请在此输入您的代码
def Findroot(x):
    # 不断循环找父节点，直至父节点是自己，也就是根节点。
    if x == p[x]: return x
    p[x] = Findroot(p[x])
    return p[x]
# 合并x， y所在的集合
def Merge(x, y):
    rootx = Findroot(x)
    rooty = Findroot(y)
    p[rootx] = rooty

def Query(x, y):
    rootx = Findroot(x)
    rooty = Findroot(y)
    return rootx == rooty

n, q = map(int, input().split())
p = list(range(n + 1))
for _ in range(q):
    op, x, y = map(int, input().split())
    if op == 1:
        Merge(x, y)
    else:
        if Query(x, y):
            print("YES")
        else:
            print("NO")

单调栈

基础概念

单调栈:满足单调性质的栈

实现:插入新元素时，将不满足单调性质的元素弹出即可

维持一个递减的单调栈

3，1满足单调递减性质，放入单调栈

312不满足单调递减，2把1弹开，放入2

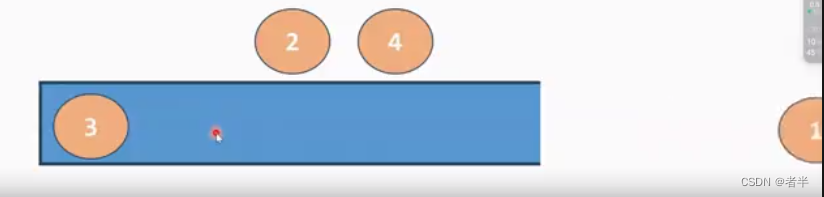
3，2，4和3，4都不满足单调递减，4把2，3踢出去。

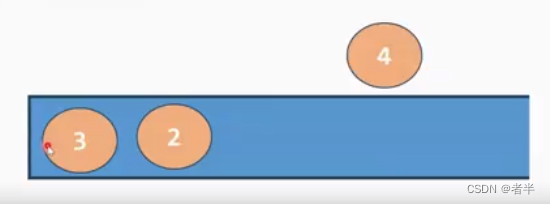
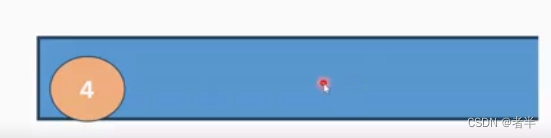
什么时候结束呢？

直到满足单调性质停止

维护这个有什么用呢？

回顾上面过程，因为2>1，所以2把1挤出去了。

也就是可以求出右侧第一个大于自己的元素。

蓝桥1142模板题

def right_bigger(a, n):
    ans = [-1] * n
    stack = []
    for i, x in enumerate(a):
        # 当栈顶元素小于x，则此时要弹出
        while len(stack) != 0 and a[stack[-1]] < x:
            # 把栈顶弹出
            ans[stack[-1]] = i + 1 # 答案记录的时候加一
            stack.pop()
        stack.append(i)
    return ans

def left_bigger(a, n):
    ans = [-1] * n
    stack = []
    for i in range(n - 1, -1, -1):
        x = a[i]
        # 当栈顶元素小于x，则此时要弹出
        while len(stack) != 0 and a[stack[-1]] < x:
            # 把栈顶弹出
            ans[stack[-1]] = i + 1 # 答案记录的时候加一
            stack.pop()
        stack.append(i)
    return ans

N = int(input())
h = list(map(int, input().split()))
print(*left_bigger(h, N))
print(*right_bigger(h, N))

在 Python 中，*可以用于在函数调用中进行解包（unpacking）操作。在 print 函数中，* 可以将序列（比如列表、元组等）解包为单独的参数，从而使得每个序列元素都成为独立的参数传递给 print`函数。

举个例子，假设有一个列表 my_list = [1, 2, 3]，如果你想将列表中的元素作为独立的参数传递给 print 函数，可以使用 * 进行解包操作，如下所示：
print(*my_list)

上述代码等价于以下代码：
print(1, 2, 3)

这样就会以空格分隔的形式打印出列表中的元素。