目录
一、简介
二、优缺点介绍
三、Python代码示例
四、总结
一、简介
K-Means算法是一种经典的无监督学习算法,用于将数据集中的样本分为 K 个不同的类别。K-均值聚类算法的工作原理如下:
- 随机选择 K 个中心点作为初始聚类中心。
- 将每个样本点分配到离其最近的聚类中心,形成 K 个初始聚类。
- 通过计算每个聚类中心的均值,更新聚类中心的位置。
- 重复步骤2和步骤3,直到聚类中心不再发生变化或达到预定迭代次数。
二、优缺点介绍
优点:
- 实现简单,计算快速,适用于处理大规模数据集。
- 可用于聚类分析,发现数据中的隐藏模式和组织结构。
- 算法的结果具有可解释性,即每个样本点都属于唯一的一个聚类。
缺点:
- 需要预先指定聚类数量 K,这对于一些数据集来说可能是困难的,而错误的选择聚类数量可能导致结果不准确。
- 对初始聚类中心的选择敏感,初始点的选择不同可能导致得到不同的聚类结果。
- 对于非凸形状的聚类,K-均值算法可能表现不佳,会将非凸形状的聚类误认为多个凸形状的聚类。
三、Python代码示例
1.K-Means类代码:
import numpy as np
class KMeans:
def __init__(self, n_clusters=2, max_iters=100):
self.n_clusters = n_clusters
self.max_iters = max_iters
def fit(self, X):
# 随机初始化聚类中心
self.centroids = X[np.random.choice(range(len(X)), self.n_clusters, replace=False)]
for _ in range(self.max_iters):
# 分配样本到最近的聚类中心
clusters = [[] for _ in range(self.n_clusters)]
for x in X:
distances = [np.linalg.norm(x - centroid) for centroid in self.centroids]
closest_cluster = np.argmin(distances)
clusters[closest_cluster].append(x)
# 更新聚类中心
new_centroids = []
for cluster in clusters:
new_centroids.append(np.mean(cluster, axis=0))
new_centroids = np.array(new_centroids)
# 判断聚类中心是否变化不再变化,如果是则停止迭代
if np.all(self.centroids == new_centroids):
break
self.centroids = new_centroids
def predict(self, X):
predictions = []
for x in X:
distances = [np.linalg.norm(x - centroid) for centroid in self.centroids]
closest_cluster = np.argmin(distances)
predictions.append(closest_cluster)
return predictions
2.调用代码
from Kmeans import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 生成样本数据
X, y = make_blobs(n_samples=200, centers=4, random_state=0)
# 实例化KMeans对象,并进行训练和预测
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
predictions = kmeans.predict(X)
# 绘制聚类结果
plt.scatter(X[:, 0], X[:, 1], c=predictions)
plt.scatter(kmeans.centroids[:, 0], kmeans.centroids[:, 1], c='red', marker='X')
plt.show()
plt.savefig(fname="Kmeans_result.png")
3.效果
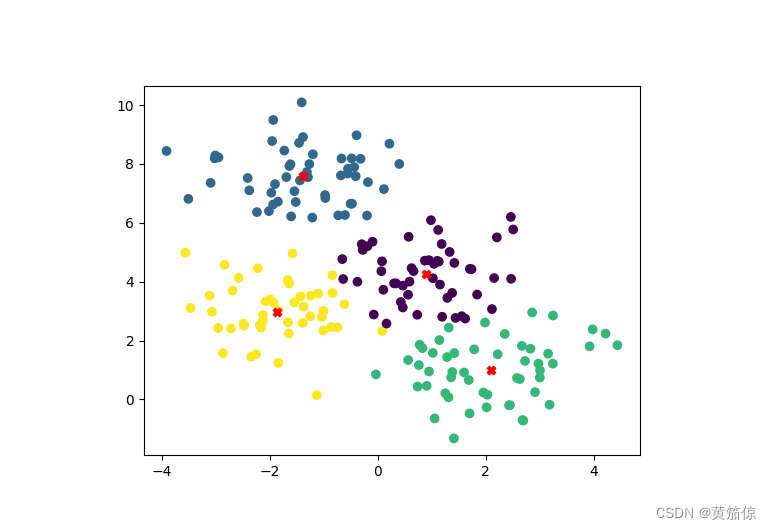
下方InsCode选择查看文件里的Kmeans_result.png即可查看可视化结果
四、总结
K-均值聚类算法是一种简单而高效的聚类算法,适用于处理大规模数据集。但需要注意选择合适的聚类数量和初始聚类中心,以及对数据集的形状有一定的限制。