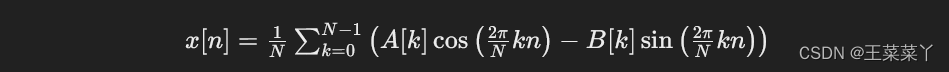傅里叶级数（Fourier Series）和傅里叶变换（Fourier Transform）都是以法国数学家让-巴蒂斯特·约瑟夫·傅里叶的名字命名，用于分析函数或信号的频率成分，它们基于相似的数学原理，但是应用于不同类型的函数和信号，解决的问题也有所不同。
傅里叶级数
傅里叶级数用于分解周期性函数或信号为一系列正弦和余弦函数的和。每个正弦和余弦函数都有特定的频率，这些频率是基础频率的整数倍，也就是谐波。傅里叶级数允许我们精确地表达周期性波形，无论其形状多么复杂。
对于周期为T的函数f(t)，其傅里叶级数表达式为：
其中，an和bn是傅里叶系数，表示各个谐波成分的幅度。
傅里叶变换
傅里叶变换将非周期性函数或信号转换成频率域的表示形式。这种转换是连续的，允许我们分析和理解非周期函数或信号的频率组成。傅里叶变换特别适用于分析具有复杂频率成分的信号，如音乐、图像和其他形式的数据。
其中，ω是角频率，F(ω)表示频率域中的复数形式，包含了幅度和相位信息。
主要区别
应用对象：傅里叶级数适用于周期性函数或信号，而傅里叶变换适用于非周期性函数或信号。
表示形式：傅里叶级数以一系列离散的正弦和余弦波形式表示周期信号，傅里叶变换则将非周期信号表示为连续的频率谱。
数学形式：傅里叶级数使用和（求和）表示，涉及整数倍频率的正弦和余弦函数；傅里叶变换则是一个积分形式，涉及连续频率谱。
傅里叶级数—>连续傅里叶变换
傅里叶级数到傅里叶变换的扩展是通过考虑非周期性信号或者说周期无限大的信号来实现的。这个过程体现了从分析周期性函数的离散频率分量到分析非周期性函数的连续频率谱的过渡。
- 周期性到非周期性：考虑一个周期性函数的周期TT趋向于无限大时，这个函数实际上变成了一个非周期性函数。在这种情况下，傅里叶级数中的离散频率分量将转换为连续频率分量。
- 离散到连续：随着周期的无限扩大，原本离散的频率分量（基频及其整数倍）将填满整个频率范围，形成一个连续的频率谱。这种过渡可以通过考虑频率间隔逐渐变小，直到变成连续频率谱的过程来理解。
- 和到积分：在傅里叶级数中，对各个频率分量求和的过程，在周期趋向无限大时，转变为对连续频率分量进行积分的过程，即傅里叶变换。
傅里叶级数—>离散傅里叶变换
傅里叶级数到离散傅里叶变换（DFT）的扩展是通过考虑离散时间信号的处理来实现的。
当我们处理的信号是离散的，并且希望在离散的频率域进行分析时，使用离散傅里叶变换（DFT）。DFT将离散时间信号转换为离散频率域的表示。对于一个长度为N的离散时间序列x[n]，其DFT定义为：
其中，X[k] 是离散频率域的表示，k是离散频率的索引。
- 离散时间信号：考虑数字信号处理中的应用，我们处理的信号通常是离散时间信号。这要求我们从连续信号的分析转向离散信号的分析。
- 周期性和有限长度：离散时间信号通常具有有限长度，这要求对信号进行某种形式的周期扩展或假设，以便使用周期性分析工具。DFT实际上是在对信号进行周期扩展的假设下，将傅里叶级数的概念应用于离散信号。
- 离散频率域：由于信号本身是离散的，其频率域的表示也是离散的。DFT提供了一种将离散时间信号转换为离散频率域表示的方法，反映了信号在不同离散频率上的幅度和相位信息。
- 计算效率：为了提高计算效率，尤其是对于长序列的离散傅里叶变换，快速傅里叶变换（FFT）算法被开发出来。FFT是DFT的一种算法实现，能够显著减少计算时间。
利用欧拉公式将上述DFT公式变成一系列正弦余弦函数之和
对于长度为 N 的离散时间序列 x[n]，其DFT定义为：
应用欧拉公式，可以将指数形式展开为：
于 cos(−θ)=cos(θ) 和 sin(−θ)=−sin(θ)，上式可以进一步简化为：
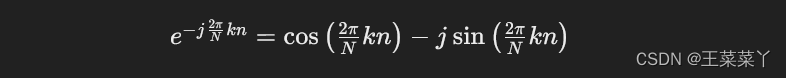因此，DFT的表达式变为：
离散傅里叶逆变换
离散傅里叶逆变换（IDFT）允许我们从频率域的表示 X[k] 重构回时域的信号 x[n]。IDFT 的定义公式为：
其中，N 是序列的长度，n 是时域中的样本索引，k是频率域中的索引。
利用欧拉公式将上述IDFT公式变成一系列正弦余弦函数之和
利用欧拉公式 e^jθ=cos(θ)+jsin(θ)，可以将上述公式中的复指数项展开成正弦和余弦项。这样，IDFT公式变为：
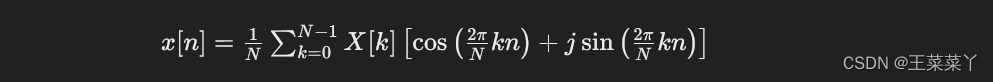接下来，我们需要进一步展开X[k]。由于 X[k] 是一个复数，可以表示为 X[k]=A[k]+jB[k]，其中 A[k]和 B[k]分别是 X[k] 的实部和虚部。将 X[k] 的这种表示形式代入上述IDFT公式中：
将上式中的实部和虚部分开，得：
由于 x[n] 是一个实数序列（假设原始信号是实数），我们只关心上式的实部。因此，IDFT可以使用正弦和余弦函数表示为：
