本文旨在讲解布隆过滤器的原理以及实现方式,希望通过本文能使读者对布隆过滤器有一定的认识!
一、布隆过滤器的引入
在讲解布隆过滤器之前,我们还是先提及一下前面讲的位图行,位图可以处理大量的数据,广泛用于查找等操作!但是对于位图而言,起能处理的类型只能是整形,那么对于字符串等其他类型位图是无法处理的,那么这时就引进了我们下面要讲的布隆过滤器!
下面来介绍什么是布隆器,正如前面说的,位图不能处理字符串等类型,那么我们该怎么办呢,因为我们前面学习过哈希,所以我们可以使用哈希的思想将字符串类型先转化为整形,利用哈希将字符串转化为整形的方法有很多,下面来看一下常见的几种字符串哈希算法。
字符串哈希算法:
1.BKDRhash

该算法就是该字符串的每个字符的ascii码值乘上一个数,然后再进行相加!
2. SDBMhash

3.DJBhash

4.APhash

通过观察上述字符串哈希,我们可以发现,基本上都是字符串中的每一位乘上一个数然后进行获取最终结果的 。
布隆过滤器的介绍以及应用场景!
既然介绍了这些字符串哈希函数,那么我们就来讲一下布隆过滤器是如何诞生以及实现的,上面已经提到了,因为位图不能处理非整形的数据,那么面对一个非整形的数据,我们就需要进行一次哈希函数将其转化为整形,然后再进行映射到地址中去,但是对于字符串哈希函数,我们很难保证没有不同的字符串对应有相同的数字,此时再进行某一位的映射时,就会导致误差!例如:
 对于上图,如果middle与end的对应的整形相同,那么就会映射在同一块区域,那么当end不存在的时候,但是middle存在的时候,就会导致误判,误判end也存在!这时有人就想出来将一个字符串对应多个哈希函数,这样误判会不会结束呢?答案是否定的!误判是肯定不会不存在的!但是会减少!字符串与对应值有着多对一的关系。我们也可以发现,这种误判只会出现在‘存在的情况!’对于“不存在”的情况,是一定准确的!所以就有人说了,那么发明这种东西有什么用呢?这时我们的大佬布隆在发明他的时候已经想到了应用场景,即其可以筛选一定的情况,从而加快查找的速率!
对于上图,如果middle与end的对应的整形相同,那么就会映射在同一块区域,那么当end不存在的时候,但是middle存在的时候,就会导致误判,误判end也存在!这时有人就想出来将一个字符串对应多个哈希函数,这样误判会不会结束呢?答案是否定的!误判是肯定不会不存在的!但是会减少!字符串与对应值有着多对一的关系。我们也可以发现,这种误判只会出现在‘存在的情况!’对于“不存在”的情况,是一定准确的!所以就有人说了,那么发明这种东西有什么用呢?这时我们的大佬布隆在发明他的时候已经想到了应用场景,即其可以筛选一定的情况,从而加快查找的速率!
布隆过滤器的应用:
我们平时都玩过游戏,有很多游戏都需要用户自己定义自己的名字,但是还不能有重名的情况!对于游戏中所有的用户名,全部都存储在服务器中的数据库中,但是如果我们每次起一个名字,都要去访问服务器中的数据库,那岂不是太浪费时间了!

上图就是我们起一个名字的时候,当我们点击提交昵称的时候,会自动取服务器中的数据库中进行查询,如果查询到了有重复,就会给用户提示改昵称已经存在了,请在换个名字,这时,每当用户起一个名字那岂不是都得取服务器中的数据库进行查找一番么?
对与此问题,我们布隆大佬就想到,为何不在二者之间加上一个布隆过滤器呢,可以大大减少我们的查找时间呀!
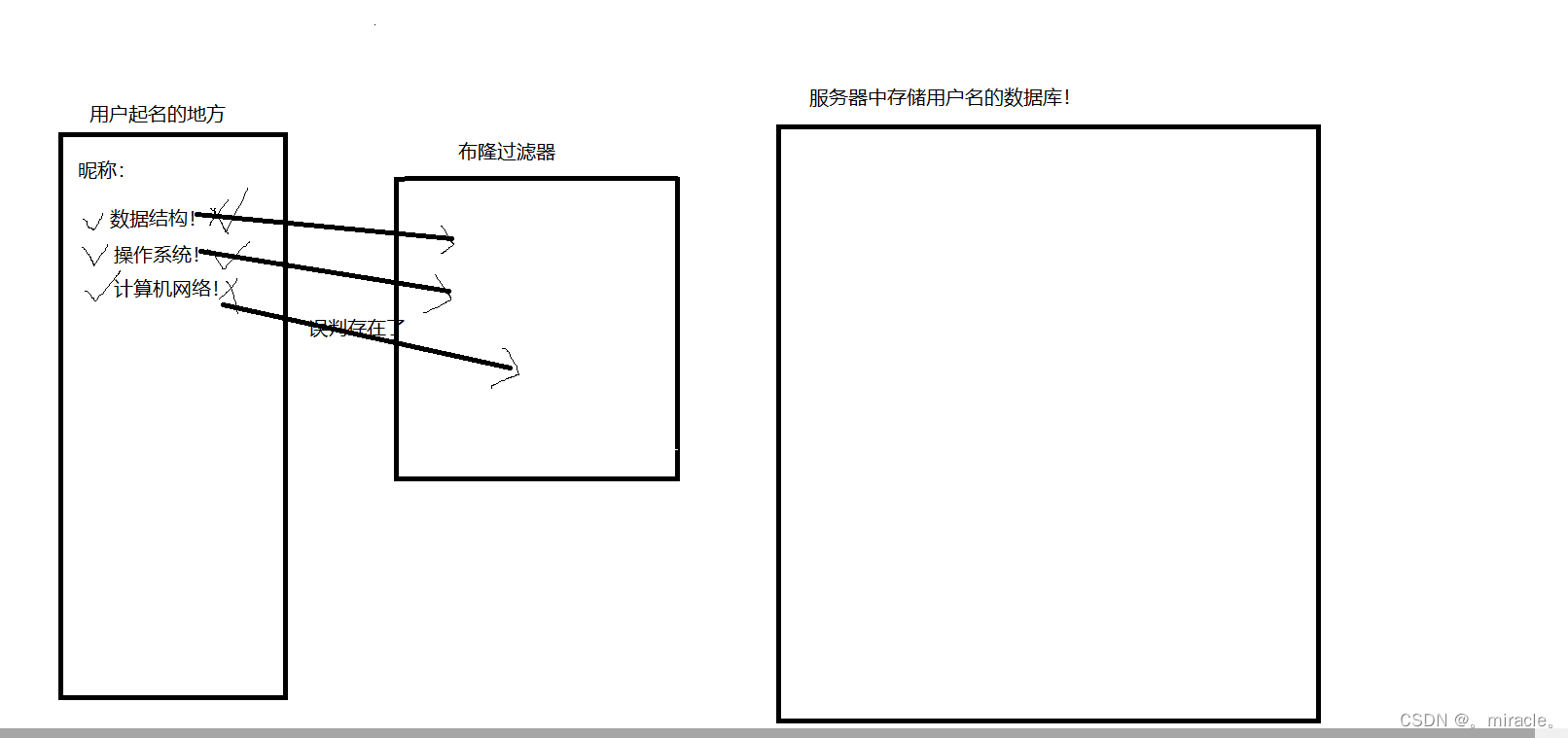 当添加过了布隆过滤器的时候,我们可以不用访问服务器中的数据库,直接通过布隆过滤器的返回结果进行判断,就像我们输入昵称的时候,还没有点击提交的时候,昵称旁边就是出现对号或错号的提示!这其实就是利用了布隆过滤器!但是布隆过滤器也存在问题,就是其结果只能准确的判断一个字符不存在,对与存在的情况,会出现误判,但是这时如果有的玩家好奇心强,我起了十个名字,8个不能用,我非得查一查这些名字都是谁在用,不查不知道,一查吓一跳,有的昵称竟然不存在也不让我起!必须反手一波举报,于是针对布隆过滤器的特性,我们增加一下条件即可!对于布隆过滤器中返回存在的昵称,因为其不一定准确,所以我们将这些昵称读取到服务器中即可!再次进行一次准确的检查再反馈给用户即可!
当添加过了布隆过滤器的时候,我们可以不用访问服务器中的数据库,直接通过布隆过滤器的返回结果进行判断,就像我们输入昵称的时候,还没有点击提交的时候,昵称旁边就是出现对号或错号的提示!这其实就是利用了布隆过滤器!但是布隆过滤器也存在问题,就是其结果只能准确的判断一个字符不存在,对与存在的情况,会出现误判,但是这时如果有的玩家好奇心强,我起了十个名字,8个不能用,我非得查一查这些名字都是谁在用,不查不知道,一查吓一跳,有的昵称竟然不存在也不让我起!必须反手一波举报,于是针对布隆过滤器的特性,我们增加一下条件即可!对于布隆过滤器中返回存在的昵称,因为其不一定准确,所以我们将这些昵称读取到服务器中即可!再次进行一次准确的检查再反馈给用户即可!
这样布隆过滤器的作用就起了很大的作用!大大增加了我们工作的效率!其实生活中也有很多存在使用布隆过滤器的场景,例如大量的数据中查询某一个人的信息,如果我们暴力查找,挨个去服务器中的数据库一一进行查找,那么效率会非常低下,此时我们就会先将标记某一个人的唯一信息,例如身份证号,手机号 转化为整形,再对相同的整形中进行服务器内部查询,即可快速完成查询信息!
二、布隆过滤器的实现!
既然布隆过滤器的作用以及讲解完毕,接下来我们看一下布隆过滤器是如何实现的吧!
对于布隆过滤器而言,其本质上还是一个位图,只不过该位图对应的哈希值有多个而已!所以我们只需要实现set函数,将其对应的多个位都set为1即可!!进行test的时候我们只需要将其对应的位都进行检测一波,如果有false就返回false即可,全为true再返回true,此时我们的true也不一定是准确的!因为会存在不同字符串的映射值可能相同的情况!但是我们的fasle是一定准确的!
下面就来看一下我们实现的布隆过滤器吧!
#pragma once
//布隆过滤器的实现!
//其本质上还是一个位图!
#include<string>
#include<bitset>
struct BKDRHash
{
size_t operator()(const string& key)
{
// BKDR
size_t hash = 0;
for (auto e : key)
{
hash *= 31;
hash += e;
}
return hash;
}
};
struct APHash
{
size_t operator()(const string& key)
{
size_t hash = 0;
for (size_t i = 0; i < key.size(); i++)
{
char ch = key[i];
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
};
struct DJBHash
{
size_t operator()(const string& key)
{
size_t hash = 5381;
for (auto ch : key)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
template<size_t N,class K = string,class HashFunc1 = BKDRHash,class HashFunc2 = APHash,class HashFunc3 = DJBHash>
class BloomFilter
{
public:
//set功能! 因为布隆过滤器其对应有多个映射值,所以我们使用多个哈希进行位映射!将对应的位置为1即可!!
void set(const K& x)
{
size_t hash1 = HashFunc1()(x)%N; //对N进行取余,保证其在这些空间上,防止因转化为整形过大!
size_t hash2 = HashFunc2()(x)%N; //对N进行取余,保证其在这些空间上,防止因转化为整形过大!
size_t hash3 = HashFunc3()(x)%N; //对N进行取余,保证其在这些空间上,防止因转化为整形过大!
//对三个映射的位统统进行置一处理!!
bt.set(hash1);
bt.set(hash2);
bt.set(hash3);
}
//test功能! 检测该字符是否存在,只需要将其对应的位进行test即可,如果有一个不存在直接返回false,
//当三个都存在返回true即可,但是此时的true也是一种不准确的值!
bool test(const K& key)
{
size_t hash1 = HashFunc1()(key) % N; //对N进行取余,保证其在这些空间上,防止因转化为整形过大!
size_t hash2 = HashFunc2()(key) % N; //对N进行取余,保证其在这些空间上,防止因转化为整形过大!
size_t hash3 = HashFunc3()(key) % N; //对N进行取余,保证其在这些空间上,防止因转化为整形过大!
if (bt.test(hash1) == false)
{
return false;
}
else if (bt.test(hash2) == false)
{
return false;
}
else if (bt.test(hash3) == false)
{
return false;
}
//当三者都为true时,才true!但是此时的true也是一个不准确的值!
else if (bt.test(hash1) == true && bt.test(hash2) == true && bt.test(hash3) == true)
{
return true;
}
}
private:
std::bitset<N>bt; //本质上还是一个位图!
};我们首先做的就是实现三个字符串哈希函数,用于我们的字符串映射的多个值问题!
细心的小伙伴们可能发现了,我没有实现reset函数,我为什么没有实现呢?对与布隆过滤器,其大多是不支持删除的!因为一个字符可能对应多个哈希值,某一位可能与已经存在的一位相同,如果将该位删除,那么与其相同的位也会删除掉,这就会导致误删的现象,但是我们可以使用引用计数的方法来解决reset的问题!
既然我们的布隆过滤器已经实现了,那么我们就简单的进行测试一下其效果吧!

我们将“数据结构”set到过滤器中,然后找一个与其比较相似的字符串“数据结构 ”进行测试,显然其不存在于我们的过滤器中,看来我们的布隆过滤器效果还是蛮不错的嘛!
1.相似字符串的误判率
下面我们来看一下大量的相似字符串的误判率!


2.不相似字符串的误判率
我们把数据个数N调到1000来观察一下结果!
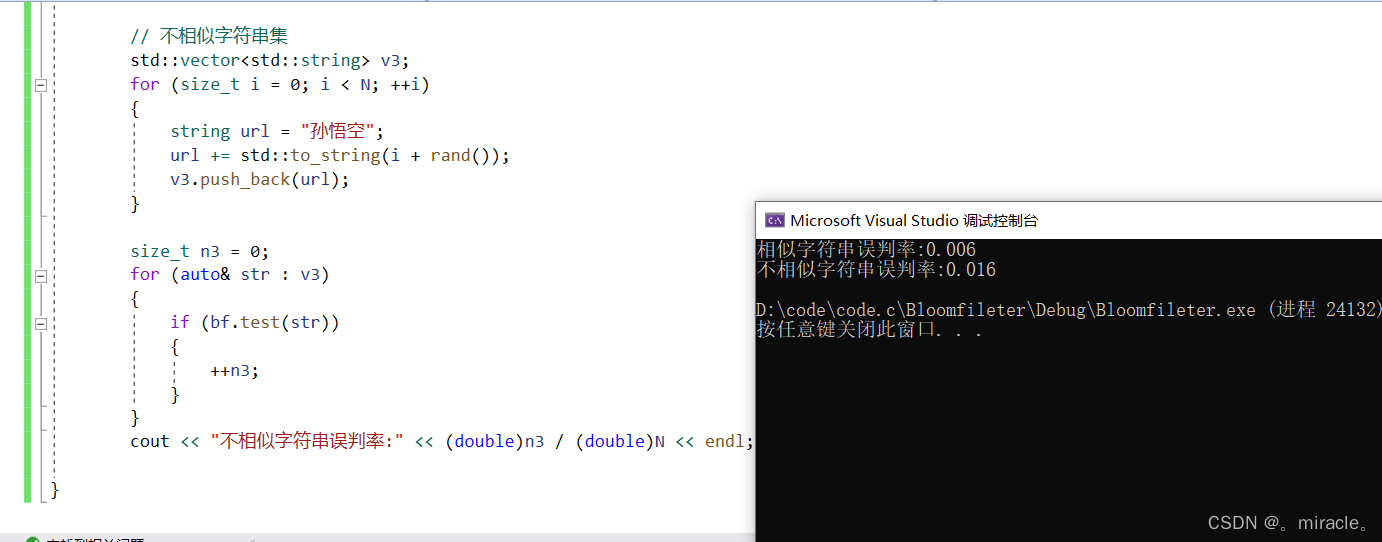
根据结果还是容易看出来:相似字符串的误判率还是比较大的,那么这个误判率与什么有关系呢?
我把文章链接贴在下面:感兴趣的小伙伴可以看一下布隆过滤器的误判率的影响!详解布隆过滤器的原理,使用场景和注意事项 - 知乎 (zhihu.com)
至此布隆过滤器的知识讲述完毕,下面来看一下另一个知识,哈希切分!
三、哈希切分
我们看一道例题来引出我们哈希切分!
例1:给定两个100亿的query,我们只有1G内存,如何快速找到两者的交集!

那么我们传统的哈希/红黑树是肯定不行的。
这时我们就可以利用hash函数将两个大文件分割成500个小文件,这时平均每个小文件占1G内存,然后对相互对应的小文件,利用set进行求交集即可! 这时就会有小伙伴问为什么要找对应的小文件呢,因为我们使用的是哈希函数,字符串相同的肯定会映射在同一个位置,那么这时该问题,不就解决了么!
但是还会存在一个小问题,就是当小文件中的内存还是比较大的话,该怎么办呢?
小文件大分两种情况:
1.都是一样的字符串,这时直接利用set进行去重既可以解决问题!
2.不是相同的字符串,这时我们只需要进行换一种哈希函数重新进行分配即可!
例2:给定一个超过100G的log file,log中存储着ip地址,求log file中最多的ip地址!
本题也是相同的道理,因为是100G的文件,所以我们仍然可以采用哈希切分的思想进行切分为小文件,然后一一处理即可!这时我们大可不必再切500个小文件,我们可以切割成100个小文件,平均一个小文件占1G内存。
我们通过对ip地址的哈希进行哈希切分,切分成100个小文件,我们的哈希函数可以是这样的!
hashi=Hash(ip)%100;
这样相同的ip地址肯定会分到相同的小文件中,这时我们对每一个小文件进行map统计次数即可!
至此,我们的布隆过滤器和哈希切分讲解完毕,希望读完本篇文章,读者能有一定的收获,也希望大大多多评论留言,互相讨论一波!